Aufgaben zur Flächenberechnung am Dreieck

Berechne den Flächeninhalt des Dreiecks $Δ A B C$ , wenn die Punkte $A$ , $B$ und $C$ folgendermaßen gegeben sind:

$A (0 | 1), B (5 | 1), C (4 | 4)$
Flächeneinheiten
Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreiecksfläche
$A_{Δ A B C} = ?$
Die Formel für die Fläche eines Dreiecks ist:
$A_{Δ A B C} = \frac{1}{2} \cdot g \cdot h$
Dabei ist $g$ die Grundlinie und $h$ die Höhe des Dreiecks.
Dreieck $Δ A B C$ im Koordinatensystem eingezeichnet:
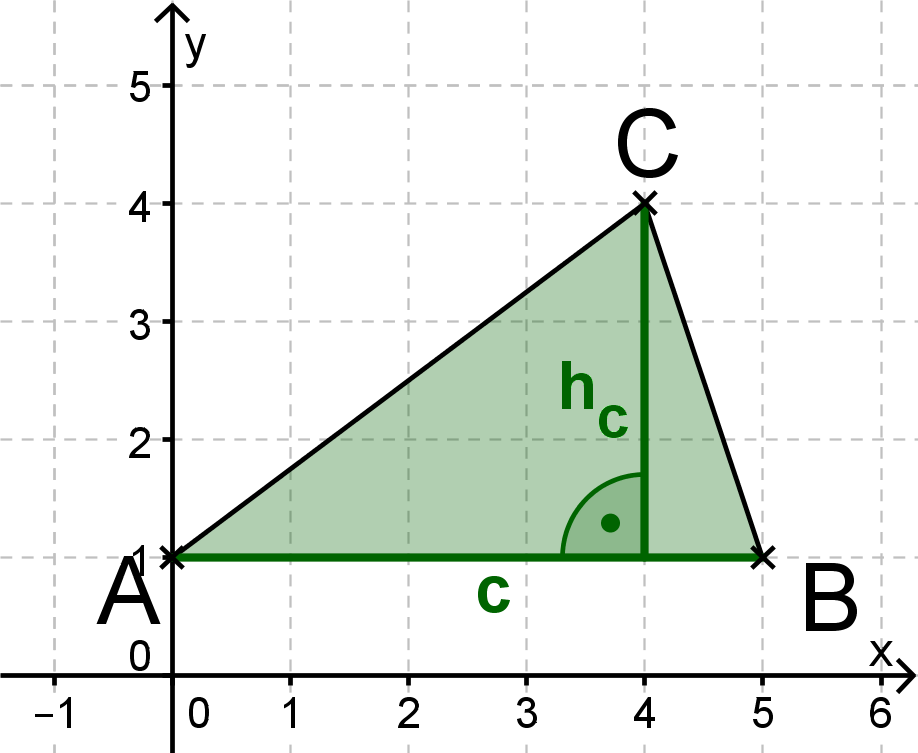
Bei dem Dreieck in dieser Aufgabe ist
$c$ parallel zur $x$ -Achse ("waagrecht" im Koordinatensystem) und
$h_{c}$ parallel zur $y$ -Achse ("senkrecht" im Koordinatensystem).
Bei solchen "gerade" im Koordinatensystem liegenden Strecken kann man die Länge leicht aus den Koordinaten berechnen; daher wählst du die Seite $c$ als Grundlinie.
$A_{Δ A B C} = \frac{1}{2} \cdot c \cdot h_{c}$
Um $c$ zu bestimmen, berechnest du die Differenz der $x$ -Koordinaten von $A$ und $B$ ,
$c = 5 - 0 = 5$
und um $h_{c}$ zu berechnen, subtrahierst du die $y$ -Koordinaten von $C$ und $A$ (oder $B$ ).
$h_{c} = 4 - 1 = 3$
Das brauchst du jetzt beides nur noch einzusetzen, und dann kannst du das Ergebnis ausrechnen.
$A_{Δ A B C} = \frac{1}{2} \cdot c \cdot h_{c} = \frac{1}{2} \cdot 5 \cdot 3 = \frac{15}{2} = 7,5$
Antwort: Die Dreiecksfläche ist $7,5$ Flächeneinheiten groß.
$A (2 | 0), B (5 | 1), C (2 | 4)$
Flächeneinheiten
Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreiecksfläche
$A_{Δ A B C} = ?$
Die Formel für die Fläche eines Dreiecks ist:
$A_{Δ A B C} = \frac{1}{2} \cdot g \cdot h$
Dabei ist $g$ die Grundlinie und $h$ die Höhe des Dreiecks.
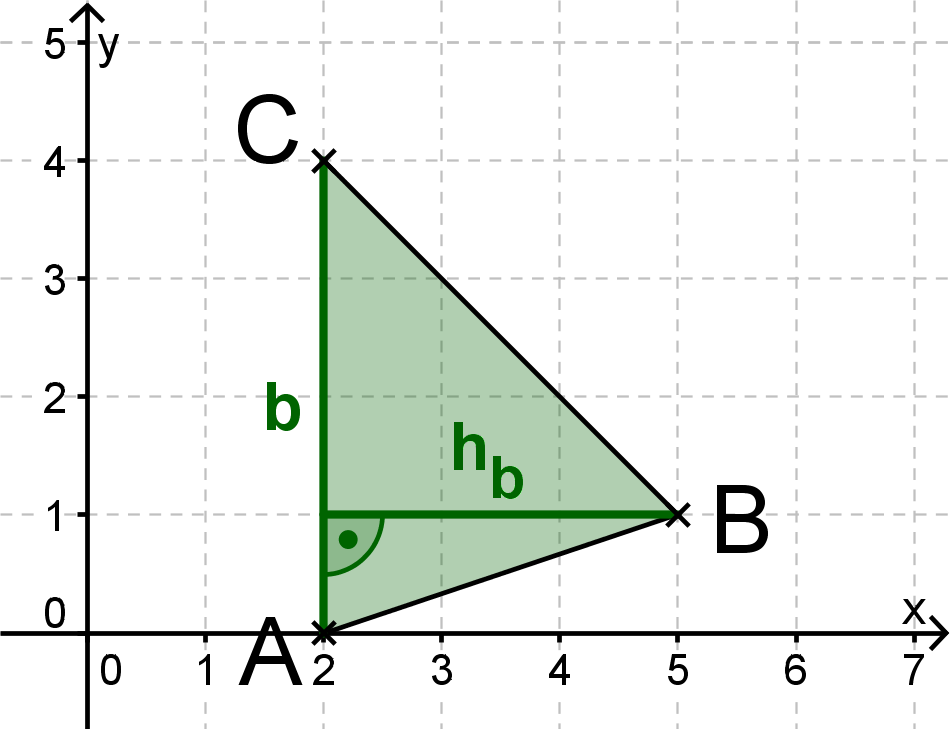
Bei dem Dreieck in dieser Aufgabe ist
$h_{b}$ parallel zur $x$ -Achse ("waagrecht" im Koordinatensystem) und
$b$ parallel zur $y$ -Achse ("senkrecht" im Koordinatensystem).
Bei solchen "gerade" im Koordinatensystem liegenden Strecken kann man die Länge leicht aus den Koordinaten berechnen; daher wählst du die Seite $b$ als Grundlinie.
$A_{Δ A B C} = \frac{1}{2} \cdot b \cdot h_{b}$
Um $b$ zu bestimmen, berechnest du die Differenz der $y$ -Koordinaten von $C$ und $A$ ,
$b = 4 - 0 = 4$
und um $h_{b}$ zu berechnen, subtrahierst du die $x$ -Koordinaten von $B$ und $A$ (oder $C$ ).
$h_{b} = 5 - 2 = 3$
Das brauchst du jetzt beides nur noch einzusetzen, und dann kannst du das Ergebnis ausrechnen.
$A_{Δ A B C} = \frac{1}{2} \cdot b \cdot h_{b} = \frac{1}{2} \cdot 4 \cdot 3 = \frac{12}{2} = 6$
Antwort: Die Dreiecksfläche ist $6$ Flächeneinheiten groß.
$A (0 | 1), B (6 | 1), C (7 | 4)$
cm²
Lösung
Zur Hilfe kannst du ein Koordinatensystem zeichnen mit
Länge der x-Achse: max. 8cm;
Länge von y-Achse: 5cm
Wähle die Grundseite des Dreiecks, bspw. die Seite $[A B]$ mit der Länge $A B = 6 cm$ .
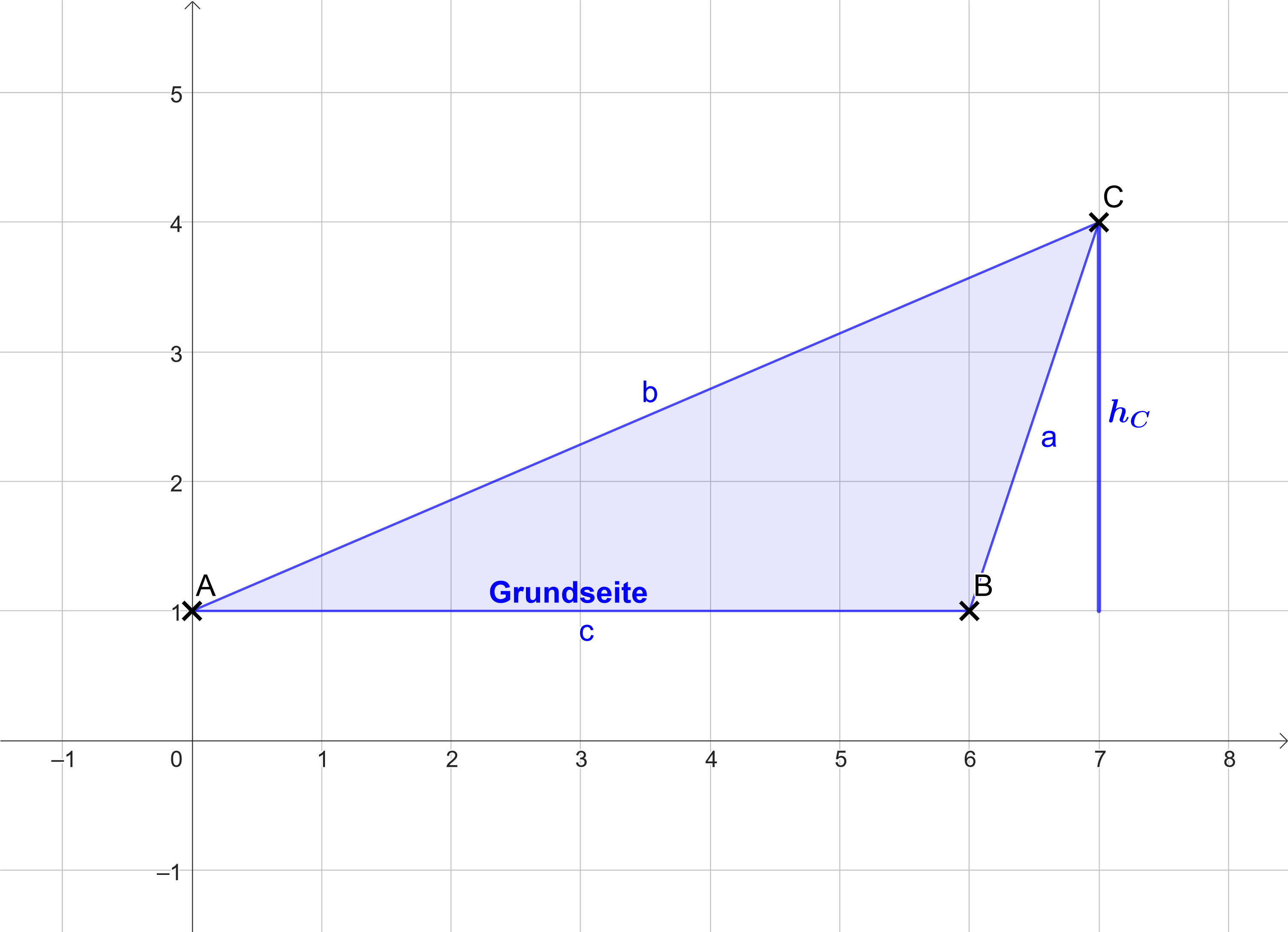
Skizze des Dreiecks
Die Höhe, in dem Fall $h_{C}$ ist $3 cm$ lang.
Mit der Formel für den Flächeninhalt des Dreiecks folgt:
$A = \frac{1}{2} g \cdot h = \frac{1}{2} \cdot 6 \cdot 3 = 9 {cm}^{2}$
Als Hilfe kannst du ein Koordinatensystem zeichnen: Länge der x-Achse: max. 8cm; Länge der y-Achse: 5cm
Bestimme die Länge der Grundseite $[A B]$ .
Bestimme die Länge der Höhe (von $C$ auf die Seite $[A B]$ ).
Wende die Formel für den Flächeninhalt an: $A = \frac{1}{2} \cdot g \cdot h$
$A (0 | 1), B (5 | 7), C (2 | 7)$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org

Aufgaben zur Flächenberechnung am Dreieck

Lösung