Aufgaben zu Winkeln

Wie groß ist die Innenwinkelsumme der folgenden Formen:

- 540°
- 360°
- 580°
- 480°
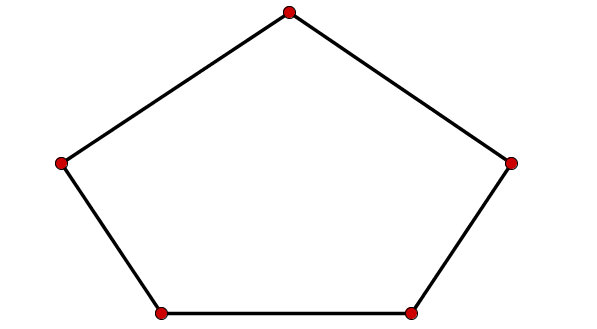
Für diese Aufgabe benötigst Du folgendes Grundwissen: Innenwinkelsumme
Die Innenwinkelsumme kann man entweder mit der Formel berechnen oder über die Zerlegung des n-Ecks in Dreiecke bestimmen.
Einerseits kann man die Innenwinkel Summe durch die Formel $(n - 2) \cdot 180^{\circ}$ errechnen. Also in dem Fall $(5 - 2) \cdot 180^{\circ} = 540 °$
Die zweite Möglichkeit ist, dass man das n-Eck in Dreiecke unterteilt. Die Dreiecke müssen dabe ihre Ecken in den Ecken des n-Ecks haben. Da ein Dreieck die Innenwinkelsumme $180 °$ hat, kann man die Innenwinkelsumme folgendermaßen betiimen:
Anzahl der Dreicke $\cdot 180 °$
Hier lässt sich das 5-Eck in $3$ solche Dreiecke zerteilen, also gilt:
$3 \cdot 180 ° = 540 °$
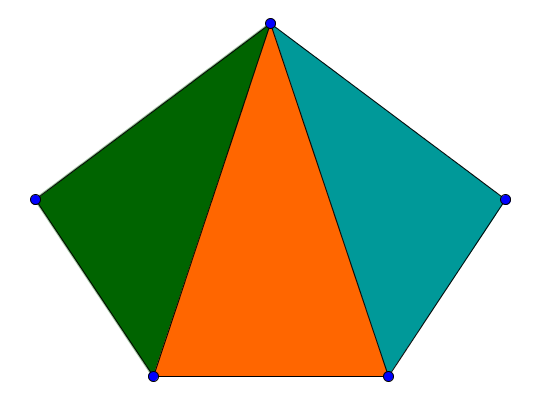
Informiere dich über die Merkmale eines Dreiecks, Vierecks und Fünfecks! Behalte das als Grundwissen.
- 1080°
- 950°
- 1250°
- 1440°
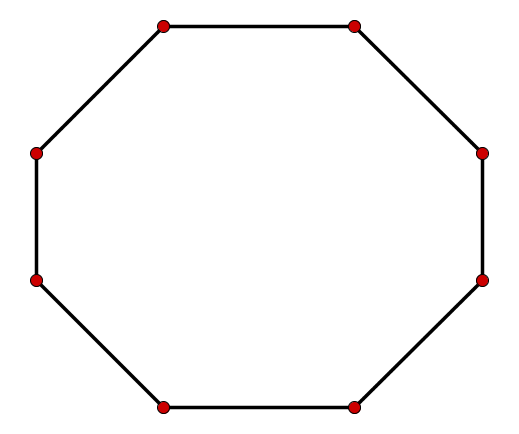
Für diese Aufgabe benötigst Du folgendes Grundwissen: Innenwinkelsumme
Unterteile das Achteck in gleich große Dreiecke. Die Dreiecke müssen dabe ihre Ecken in den Ecken des n-Ecks haben. Da ein Dreieck die Innenwinkelsumme $180 °$ hat, kann man die Innenwinkelsumme folgendermaßen bestimmen:
Anzahl der Dreicke $\cdot 180 °$
Hier lässt sich das 8-Eck in $6$ solche Dreiecke zerteilen, also gilt:
$6 \cdot 180 ° = 1080 °$
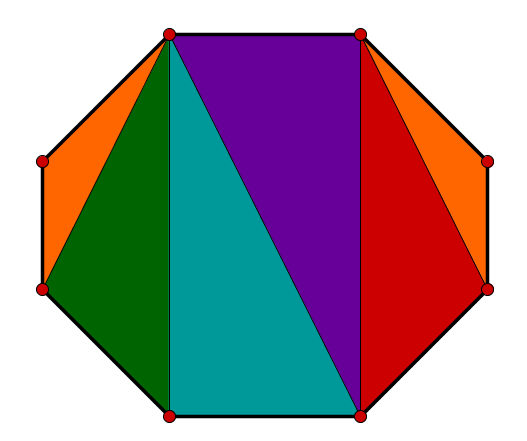
Hier kannst du das Achteck in gleich große Dreiecke zerlegen und so auf das Resultat der Innenwinkel kommen!
- 2160°
- 1800°
- 2520°
- 1980°
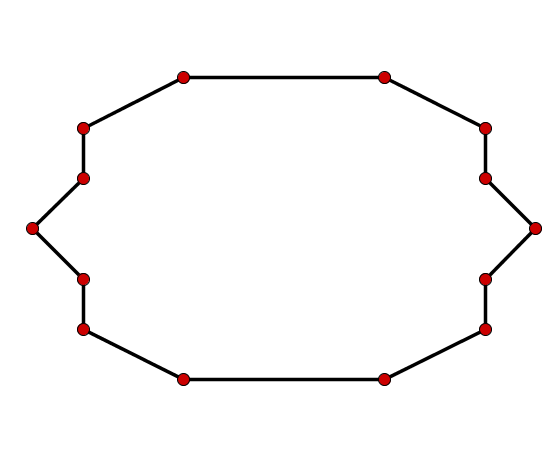
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkelsumme

Einerseits kann man die Innenwinkelsumme eines n-Ecks mit der Formel $(n - 2) \cdot 180^{\circ}$ berechnen. Also in diesem Fall mit (14 - 2) x 180 = 2160.
Die zweite Möglichkeit ist, dass man das n-Eck in Dreiecke unterteilt. Die Dreiecke müssen dabe ihre Ecken in den Ecken des n-Ecks haben. Da ein Dreieck die Innenwinkelsumme $180 °$ hat, kann man die Innenwinkelsumme folgendermaßen betiimen:
Anzahl der Dreicke $\cdot 180 °$
Hier lässt sich das 14-Eck in $12$ solche Dreiecke zerteilen, also gilt:
$12 \cdot 180 ° = 2160 °$
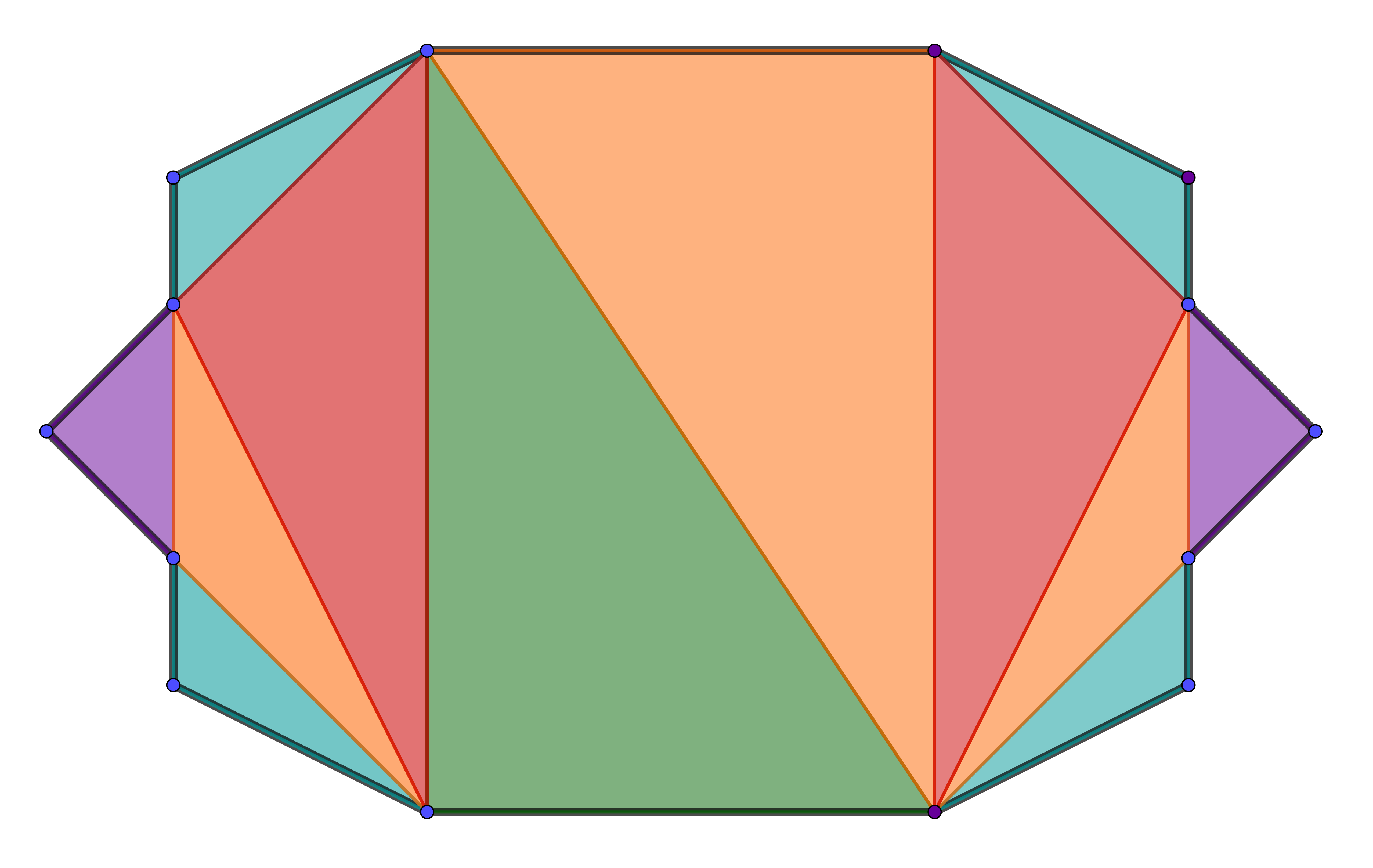
Die Winkelsumme (siehe Grundwissen!) eines n-Ecks kann man entweder mit der Formel berechnen oder sich durch Unterteilung in Dreicke herleiten.

Aufgaben zu Winkeln

﻿