Für diese Aufgabe benötigst Du folgendes Grundwissen: Satz des Pythagoras
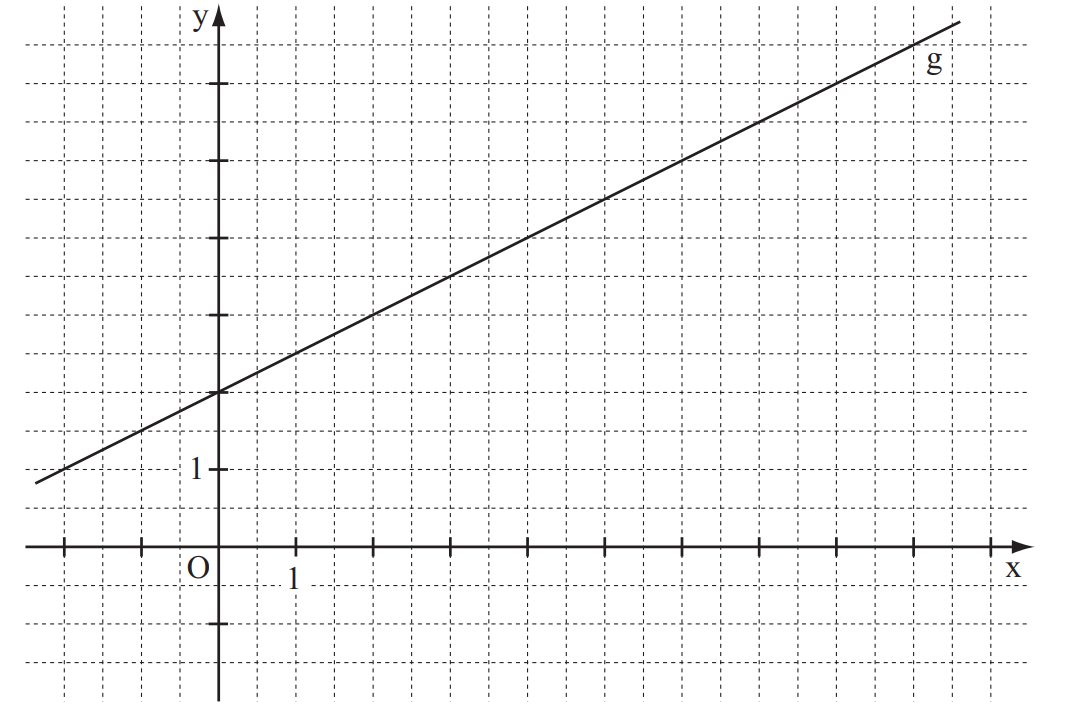
Um das erste Dreieck zu skizzieren, zeichnet man zunächst die Punkte und ein. Die Koordinaten von lassen sich ermitteln, indem man in die Funktionsgleichung der Gerade den Wert für einsetzt:
hat also die Koordinaten .
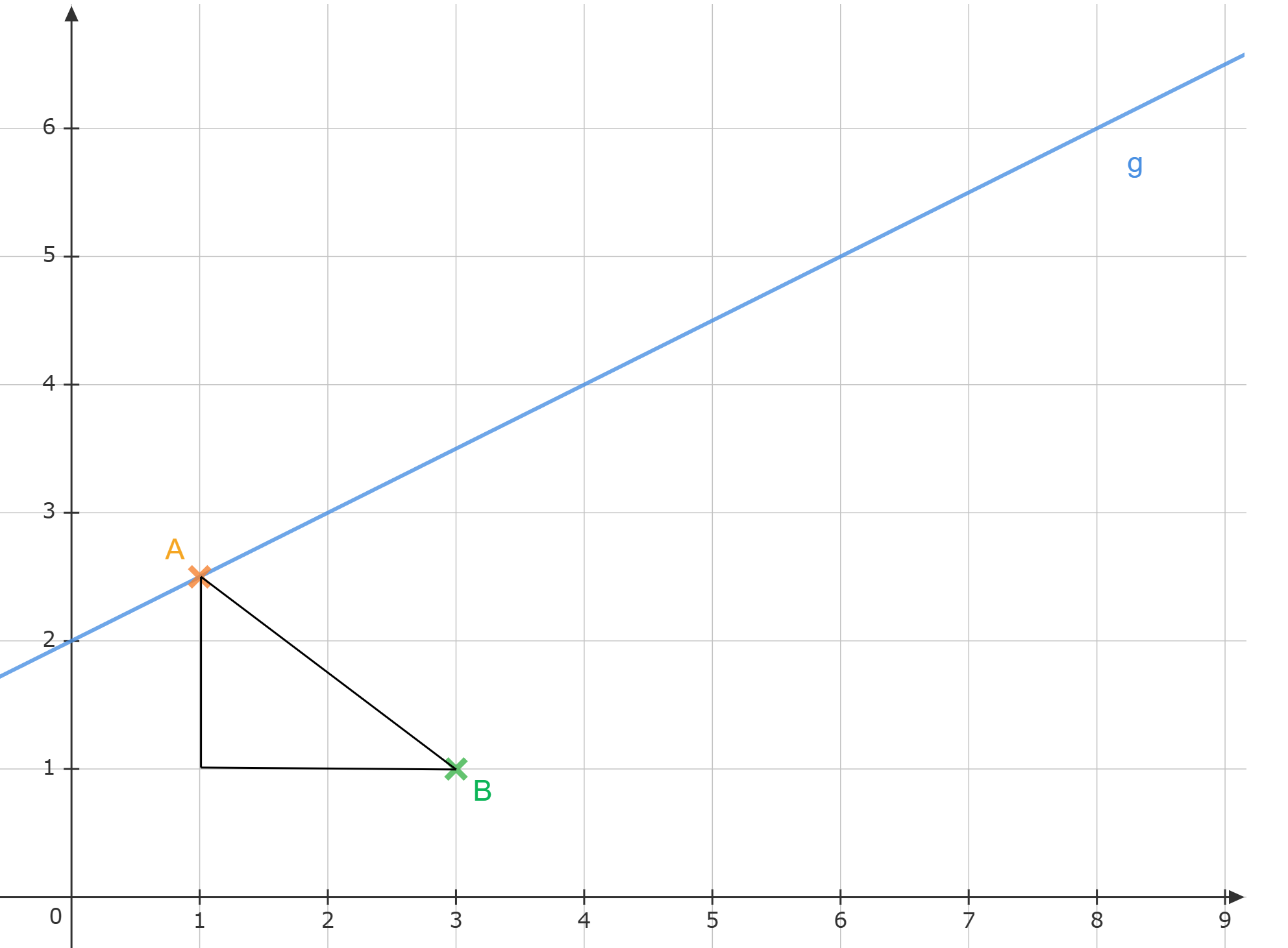
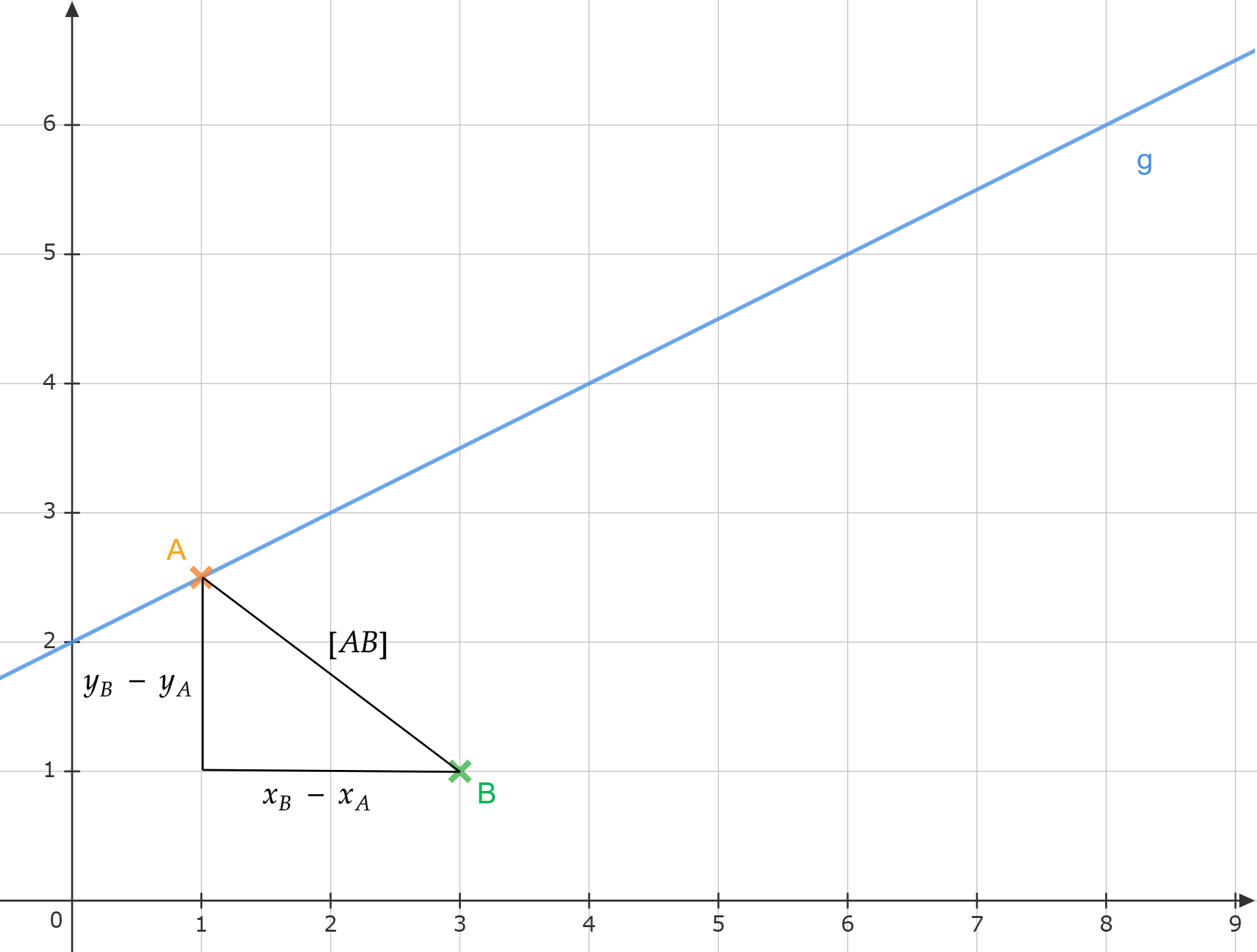
Um den Abstand zwischen den beiden Punkten zu berechnen, benutzt man den Satz des Pythagoras. Die beiden Punkte und lassen sich mit einem dritten Punkt zu einem rechtwinkligen Dreieck verbinden:
Der Abstand zwischen den beiden Punkten ist also die Hypotenuse des Dreiecks, jetzt kann man den Satz des Pythagoras anwenden:
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
Die Kathete hat eine Länge von . Die Hypotenuse muss also die Länge haben.
Da das Dreieck rechtwinklig sein muss, kann man mit dem Satz des Pythagoras die Länge der Strecke berechnen:
| | | |
| | | |
| | | |
| | | |
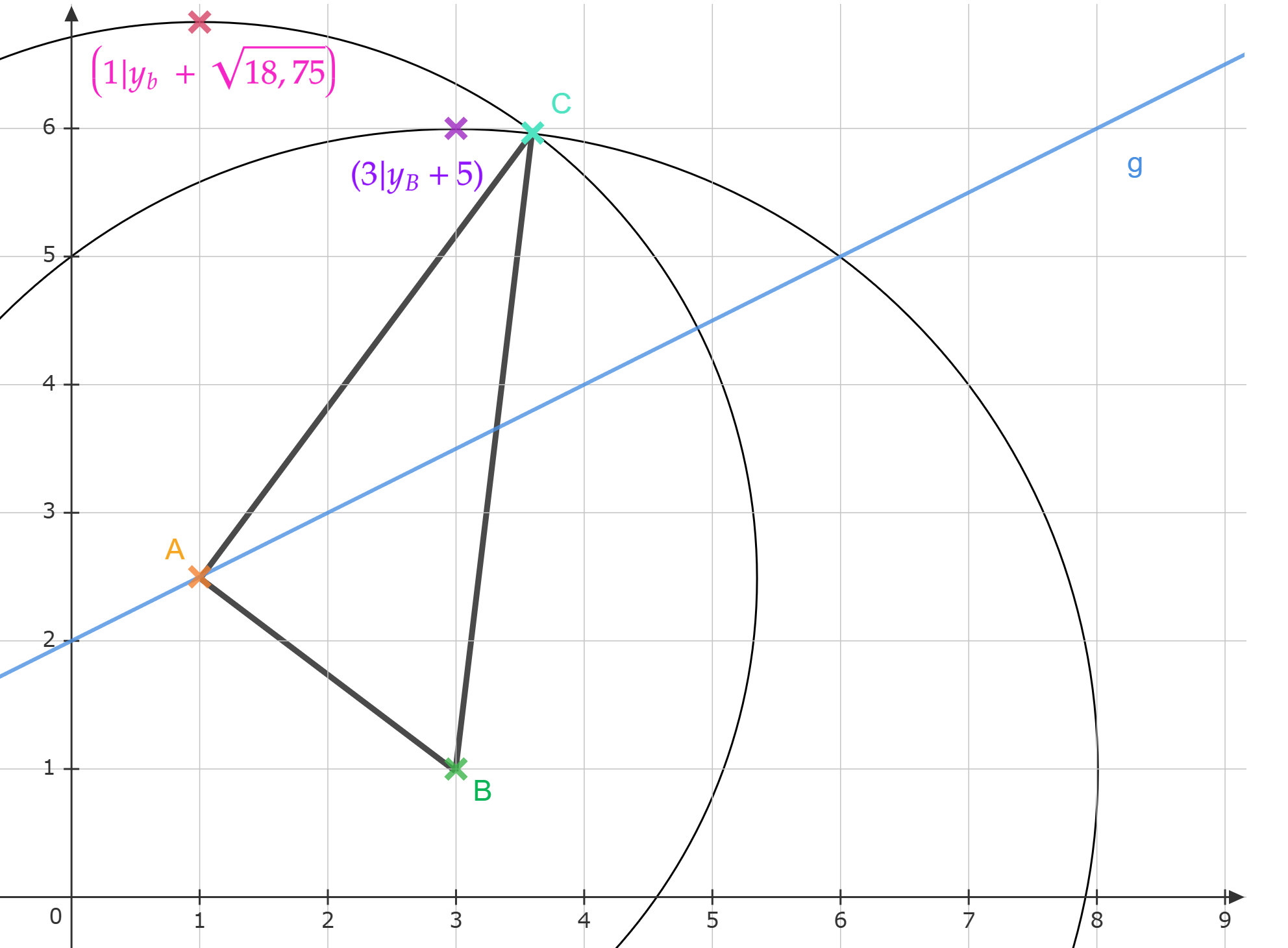
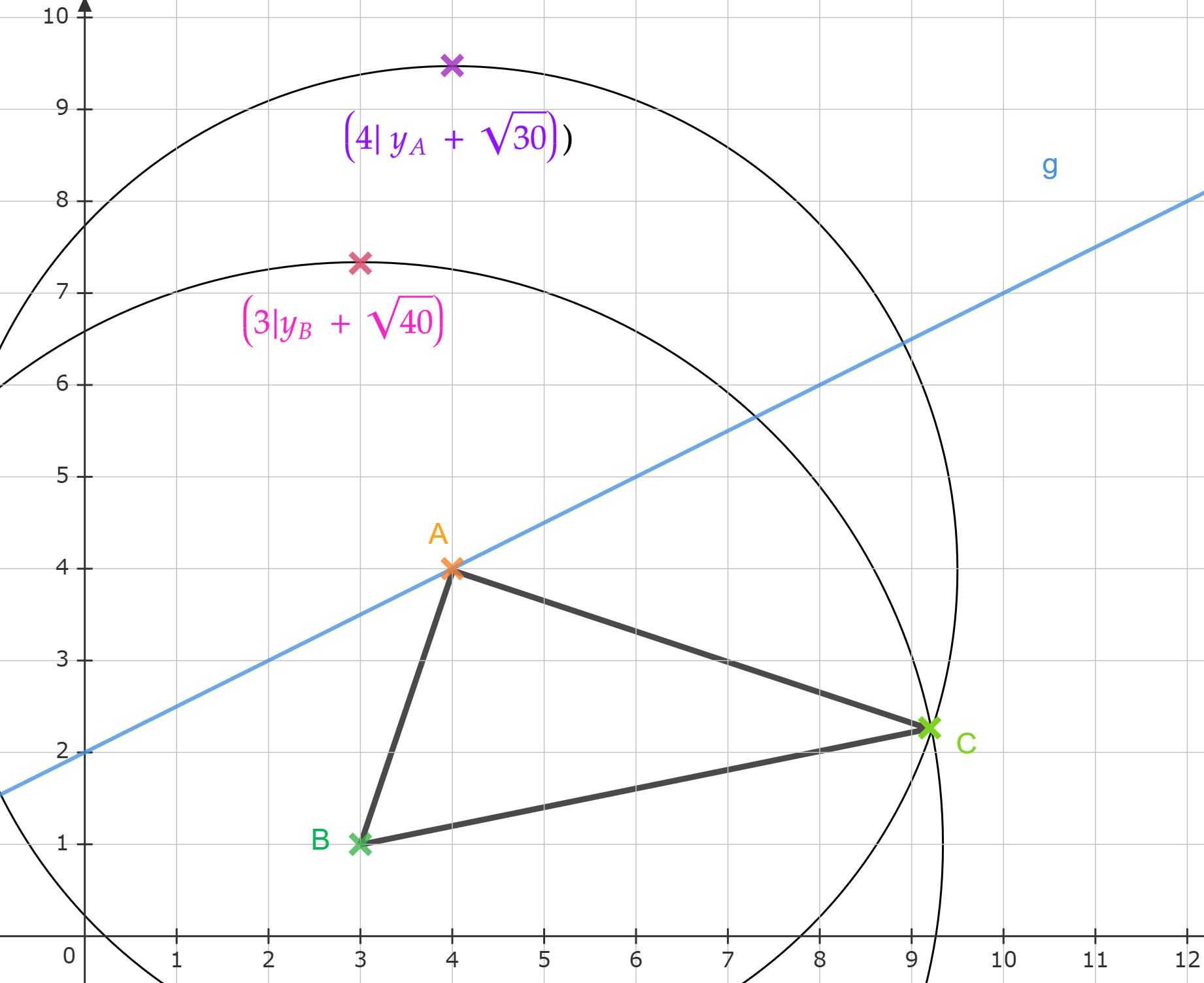
Jetzt weiß man also die Länge der drei Seiten des Dreiecks. Damit kann man die Lage von ermitteln und das Dreieck konstruieren:
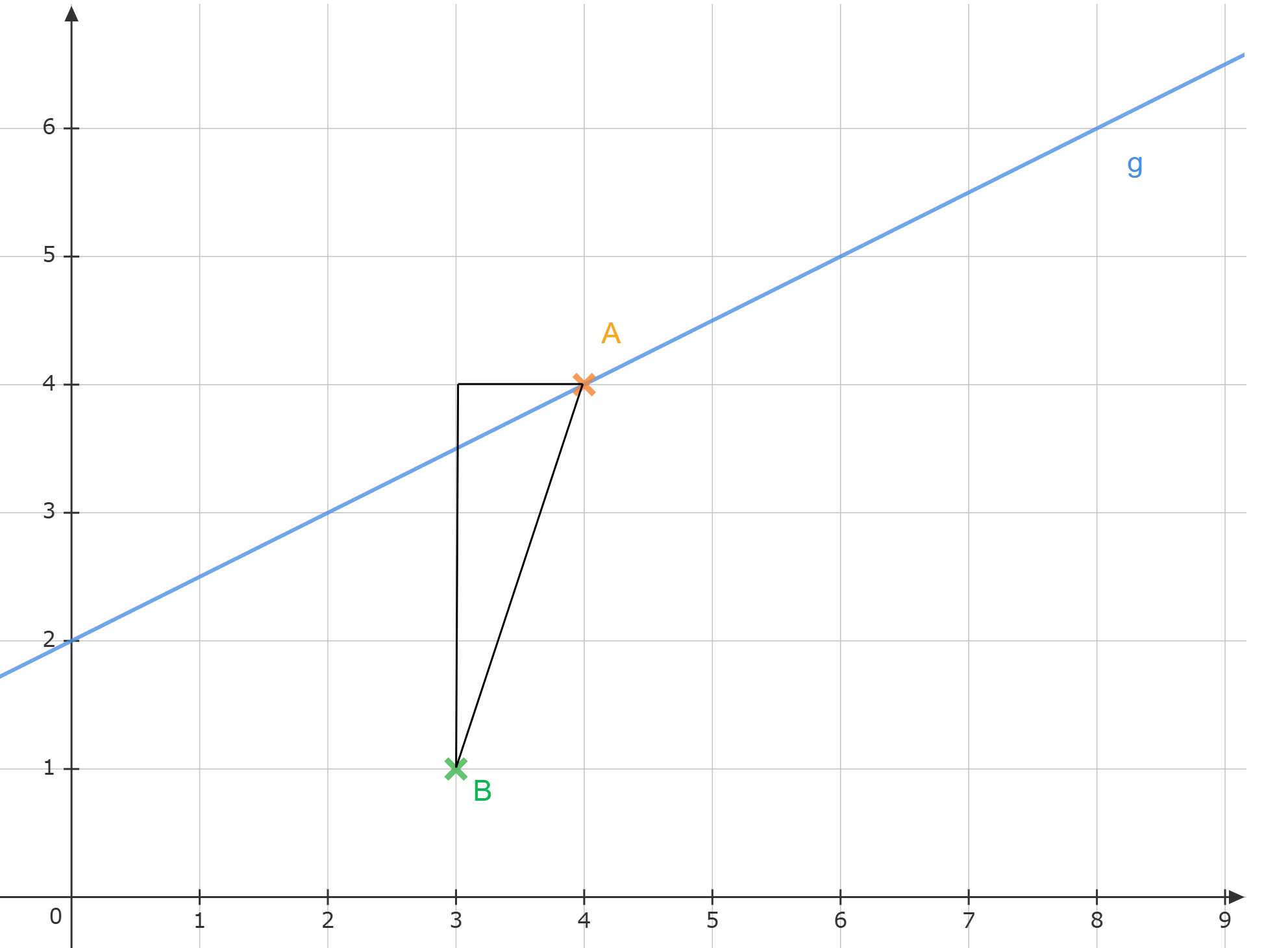
Um das zweite Dreieck zu skizzieren, zeichnet man zunächst die Punkte und ein. Die Koordinaten von lassen sich ermitteln, indem man in die Funktionsgleichung der Gerade den Wert für einsetzt:
hat also die Koordinaten .
Um den Abstand zwischen den beiden Punkten zu berechnen, benutzt man den Satz des Pythagoras. Die beiden Punkte und lassen sich mit einem dritten Punkt zu einem rechtwinkligen Dreieck verbinden:
Der Abstand zwischen den beiden Punkten ist also die Hypotenuse des Dreiecks, jetzt kann man den Satz des Pythagoras anwenden:
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
Die Kathete hat eine Länge von . Die Hypotenuse muss also die Länge haben.
Da das Dreieck rechtwinklig sein muss, kann man mit dem Satz des Pythagoras die Länge der Strecke berechnen:
| | | |
| | | |
| | | |
| | | |
Jetzt weiß man also die Länge der drei Seiten des Dreiecks. Damit kann man die Lage von ermitteln und das Dreieck konstruieren: