Teil 2, Analysis I

Ein Tipi Zelt in einem Skigebiet hat die Form eines geraden Kreiskegels, dessen Mantellinie die Länge $s = 8 m$ hat (siehe Zeichnung). Das Zelt besitzt ein Innenvolumen, das bei gleichbleibender Länge der Mantellinie von der Höhe h des Zeltes abhängt. Der jeweilige Funktionswert der Funktion $V : h \mapsto V (h)$ beschreibt dieses Innenraumvolumen.

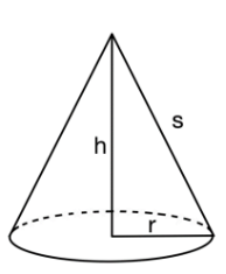
Aus optischen Gründen soll dabei die Höhe h des Tipi Zeltes mindestens 4m und maximal 6m betragen. Dabei steht h für die Höhe des Zelts in m und V(h) für das Volumen des Zelts in $m^{3}$ .

Bei den Berechnungen kann auf das Mitführen von Einheiten verzichtet werden.

Stellen Sie eine Gleichung der Funktion V auf.
(Mögliches Teilergebnis: $V (h) = - \frac{1}{3} π h^{3} + \frac{64}{3} π h$ ) (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgaben
Für das Volumen eines Kegels gilt für Radius r und Höhe h
$V = \frac{1}{3} r^{2} π h$ (Hauptbedingung)
Da diese Buchstaben direkt denen aus der Skizze entsprechen, ist hier nichts weiter zu tun.
Für das rechtwinklige Dreieck aus h, r und s=8 gilt der Satz des Pythagoras:
$r^{2} + h^{2} = 8^{2}$ (Nebenbedingung)
Forme diese Gleichung nach $r^{2}$ um, damit du in der Hauptbedingung $r^{2}$ durch einen Term in Abhängigkeit von $h$ ersetzen kannst.
$r^{2} = 64 - h^{2}$
Setze in die Hauptbedingung ein:
$V = \frac{1}{3} (64 - h^{2}) π h$
Um das Zwischenergebnis zu erhalten, musst du noch ausmultiplizieren:
$V (h) = \frac{64}{3} π h - \frac{1}{3} π h^{3}$
Gib als Hauptbedingung einen Term zur Berechnung des Kegelvolumens in Abhängigkeit von r und h an.
Als Nebenbedingung kannst du verwenden, dass r, h und s ein rechtwinkliges Dreieck mit Hypothenuse $s = 8$ bilden, wodurch der Satz des Pythagoras verwendet werden kann.
Da die Hauptbedingung am Ende in Abhängigkeit von h angegeben werden soll, kannst du die Nebenbedingung nach r auflösen. Noch besser: Löse sie nur nach $r^{2}$ auf und ersetze direkt $r^{2}$ in der Hauptbedingung.
Bestimmen Sie unter den oben genannten Vorgaben, für welche Höhe h das Tipi Zelt den maximalen Rauminhalt aufweist. Berechnen Sie für diesen Fall den Durchmesser des Bodens des Tipi Zeltes. Runden Sie Ihre Ergebnisse auf zwei Nachkommastellen. (8 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgaben
Definitionsmenge
Aus dem Text weißt du, dass die Höhe mindestens 4m und maximal 6m betragen soll. Es gilt also für die Definitionsmenge:
$D_{h} = [4; 6]$
Kandidaten für Extremstellen
An den Extremstellen hat die Steigung des Graphen von V den Wert 0. Du suchst also die Nullstellen der Ableitung von $V (h) = - \frac{1}{3} π h^{3} + \frac{64}{3} π h$ .
$V^{'} (h) = - π h^{2} + \frac{64}{3} π$
Nullstellen der Ableitung:
$V^{'} (h)$ $=$ $0$
$- π h^{2} + \frac{64}{3} π$ $=$ $0$ $+ π h^{2}$
$\frac{64}{3} π$ $=$ $π h^{2}$ $: π$
$\frac{64}{3}$ $=$ $h^{2}$
↓
Ziehe die Wurzel. Beachte, dass es zwei Lösungen gibt
$\pm \sqrt{\frac{64}{3}}$ $=$ $h$
In der Aufgabenstellung steht, dass du auf zwei Nachkommastellen runden sollst. Damit erhältst du die Werte
$h_{1} \approx 4,62$ und $h_{2} \approx - 4,62$
Da $h_{2}$ nicht in der Definitionsmenge $D_{h} = [4; 6]$ liegt, musst du diese Stelle nicht weiter beachten.
Aufgrund der Vielfachheit von 1, die die beiden gefundenen Werte haben, weißt du, dass es sich bei beiden um Extremstellen handeln muss (Alternativ: weise die Art der Extremstelle zum Beispiel mit der 2. Ableitung nach).
Funktionswerte an Extremstelle und Rändern
Bestimme die zugehörigen Volumina, indem du den Wert $h_{1} \approx 4,62$ , den linken Rand $h_{l} = 4$ und den rechten Rand $h_{r} = 6$ in die Funktion einsetzt:
$V (4,62) = - \frac{1}{3} π \cdot {4,62}^{3} + \frac{64}{3} π \cdot 4,62 \approx 206,37$
$V (4) = - \frac{1}{3} π \cdot 4^{3} + \frac{64}{3} π \cdot 4 \approx 201,06$
$V (6) = - \frac{1}{3} π \cdot 6^{3} + \frac{64}{3} π \cdot 6 \approx 175,93$
An der gefundenen Extremstelle, bei einer Tipi-Höhe von $4,62$ m hat das Zelt also das größte Volumen von $206,37 m^{3}$ .
Durchmesser des Tipis
Um den Durchmesser bestimmen zu können, brauchst du zuerst den Radius.
Setze dafür in die Nebenbedingung aus der letzten Teilaufgabe ein:
$r^{2} = 64 - h^{2}$
mit $h = 4,62$ also:
$r^{2}$ $=$ $64 - {4,62}^{2}$
$r$ $=$ $\pm \sqrt{64 - {4,62}^{2}}$
Du erhältst damit den Radius $r = 6,53$ . Die negative Lösung kannst du erneut ignorieren.
Der Durchmesser ist das Doppelte des Radius:
$d = 2 \cdot 6,53 = 13,06$
Antwort
Das Tipi hat bei einer Höhe von $4,62 m$ und einem Durchmesser von $13,06 m$ sein maximales Volumen (von $206,37 m^{3}$ ).
Gib zunächst die Definitionsmenge mithilfe der Forderungen aus der Aufgabenstellung an
Bestimme die Kandidaten für Extremstellen, indem du die Nullstellen der 1. Ableitung bestimmst
Bestimme die y-Koordinaten der Extremstellen in der Definitionsmenge.
Bestimme die Randextrema bzw. untersuche das Verhalten am Rand des Definitionsbereichs
Vergiss nicht, den Durchmesser des Zeltes anzugeben.

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das? serlo.org

$V^{'} (h)$	$=$	$0$
$- π h^{2} + \frac{64}{3} π$	$=$	$0$	$+ π h^{2}$
$\frac{64}{3} π$	$=$	$π h^{2}$	$: π$
$\frac{64}{3}$	$=$	$h^{2}$
	↓	Ziehe die Wurzel. Beachte, dass es zwei Lösungen gibt
$\pm \sqrt{\frac{64}{3}}$	$=$	$h$

$r^{2}$	$=$	$64 - {4,62}^{2}$
$r$	$=$	$\pm \sqrt{64 - {4,62}^{2}}$

Teil 2, Analysis I

Definitionsmenge

Kandidaten für Extremstellen

Funktionswerte an Extremstelle und Rändern

Durchmesser des Tipis

Antwort