Teil 2, Analysis II

Gegeben ist die Funktion f durch $f (x) = \frac{1}{12} (x^{4} - 20 x^{2} + 64)$ mit der Definitionsmenge $D_{f} = [- 3; 4,5]$ sowie die lineare Funktion $g : y = \frac{15}{4}$ mit der Definitionsmenge $D_{g} = ℝ$ .

Die Graphen der Funktion f und g in einem kartesischen Koordinatensystem werden mit $G_{f}$ bzw. $G_{g}$ bezeichnet.

Geben Sie an, ob die folgende Aussage wahr oder falsch ist, und begründen Sie Ihre Entscheidung.
"Der Graph der Funktion f ist auf $D_{f}$ achsensymmetrisch zur y-Achse." (2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsbereich
Da nur gerade Exponenten für x vorkommen und somit $f (- x) = f (x)$ gilt, könnte man meinen, dass der Graph achsensymmetrisch ist.
Allerdings ist dies aufgrund der Definitionsmenge nicht der Fall: Der Bereich rechts vom Ursprung ist größer als der links vom Ursprung (bis 4,5 bzw bis -3) und somit ist der Graph nicht symmetrisch, da links ein Teil "weggeschnitten" ist.
Hier genügt es nicht, den Funktionsterm zu untersuchen und damit Symmetrie festzustellen.
Stattdessen musst du die eingeschränkte Definitionsmenge mit in deine Überlegungen einbeziehen.
Berechnen Sie die Nullstellen der Funktion f. (5 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Substitution
Gesucht sind die Nullstellen, setze deshalb zuerst
$f (x)$ $=$ $0$
$\frac{1}{12} (x^{4} - 20 x^{2} + 64)$ $=$ $0$ $: \frac{1}{12}$
↓
Die $\frac{1}{12}$ haben keinen Einfluss auf die Nullstellen (Satz vom Nullprodukt)
$x^{4} - 20 x^{2} + 64$ $=$ $0$
Da der Term aus drei Summanden besteht, man nicht mehr ausklammern kann und der erste Exponent das Doppelte vom zweiten ist, bietet sich die Substitution an:
Ersetze $u = x^{2}$
Du erhältst:
$u^{2} - 20 u + 64 = 0$
Bestimme die Lösungen z.B. mit der Mitternachtsformel:
$u_{1 / 2} = \frac{- (- 20) \pm \sqrt{{(- 20)}^{2} - 4 \cdot 1 \cdot 64}}{2 \cdot 1}$ liefert $u_{1} = 4$ und $u_{2} = 16$
Durch die Rücksubstitution machst du aus $u_{1}$ und $u_{2}$ wieder $x$ -Werte und die Lösungen der Gleichung:
Für $u_{1} = 4$ :
$u_{1}$ $=$ $4$
↓
verwende $u = x^{2}$
$x^{2}$ $=$ $4$
↓
Ziehe die Wurzel. Vergiss nicht, dass es zwei Lösungen gibt!
$x_{1}$ $=$ $2$
$x_{2}$ $=$ $- 2$
Für $u_{2} = 16$ :
$u_{2}$ $=$ $16$
↓
verwende $u = x_{}^{2}$
$x^{2}$ $=$ $16$
↓
Ziehe die Wurzel.
$x_{3}$ $=$ $4$
$x_{4}$ $=$ $- 4$
Aufgrund der Definitionsmenge $D_{f} = [- 3; 4,5]$ sind lediglich $x_{1} = 2$ $x_{2} = - 2$ und $x_{3} = 4$ die gesuchten Nullstellen.
Verwende zur Nullstellenbestimmung die Substitutionsmethode.
Beachte anschließend die eingeschränkte Definitionsmenge!
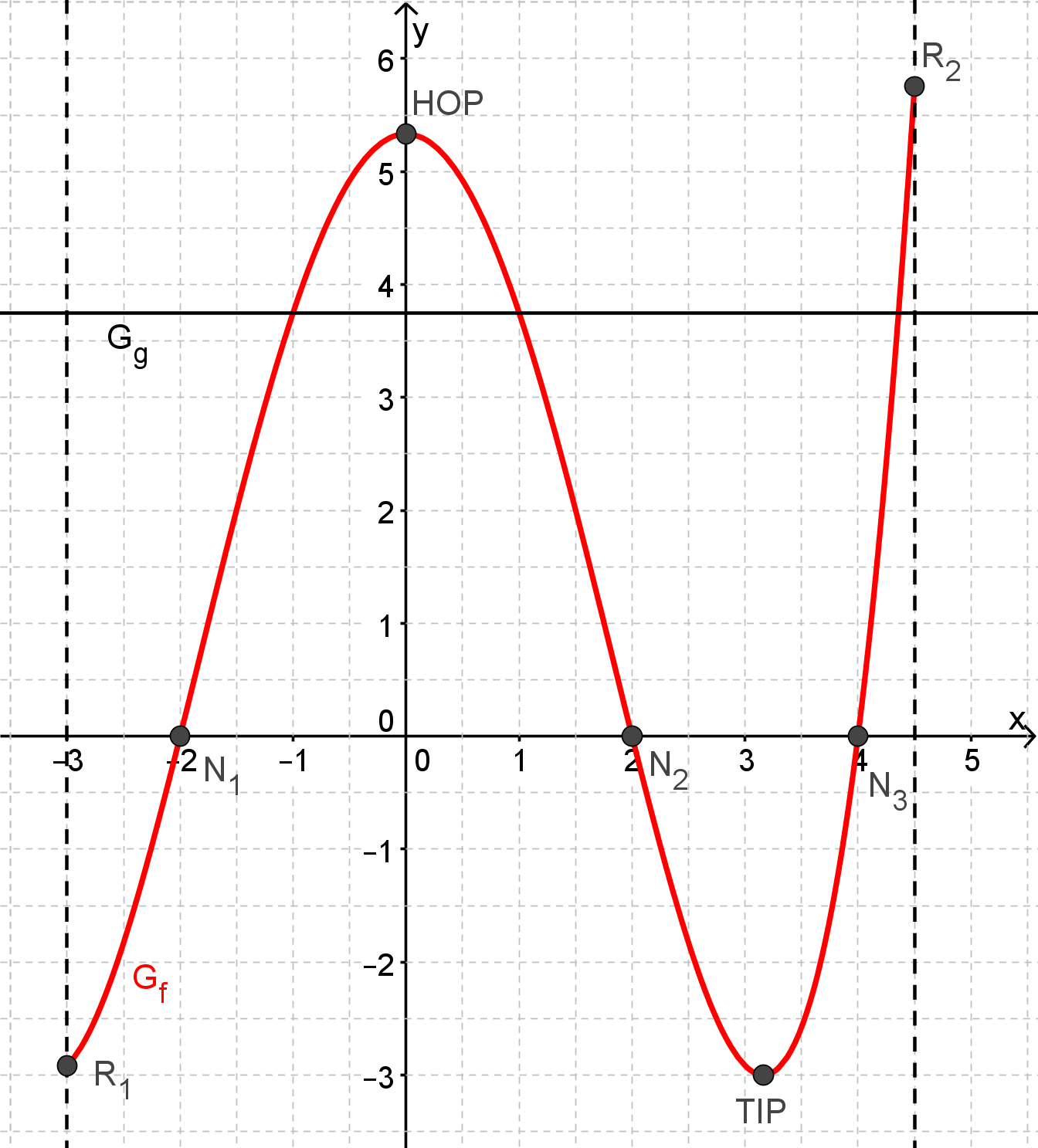
Bestimmen Sie Art und Koordinaten sämtlicher Extrempunkte von $G_{f}$ und geben Sie die Wertemenge $W_{f}$ der Funktion an. (8 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wertemenge
Randextrema
Da beide Ränder der Definitionsmenge $D_{f} = [- 3; 4,5]$ eingeschlossen sind, gibt es zwei Randextrema, deren y-Koordinaten du wie gewohnt durch Einsetzen in den Funktionsterm erhältst:
$R_{1} (- 3 | f (- 3)) \Rightarrow R_{1} (- 3 | - \frac{35}{12})$ und
$R_{2} (4,5 | f (4,5)) \Rightarrow R_{2} (4,5 | \frac{1105}{192})$
Ob es sich dabei um Randhoch- oder Tiefpunkte handelt, kannst du erst entscheiden, nachdem du die anderen Extremstellen bzw. das Monotonieverhalten untersucht hast.
Extremstellen bestimmen
Bestimme die erste Ableitung von $f (x) = \frac{1}{12} (x^{4} - 20 x^{2} + 64)$ :
$f^{'} (x) = \frac{1}{12} (4 x^{3} - 40 x)$
Bestimme nun die Nullstellen der Ableitungsfunktion, um die Kandidaten für Extremstellen zu finden:
$f^{'} (x)$ $=$ $0$
$\frac{1}{12} (4 x^{3} - 40 x)$ $=$ $0$
↓
Klammere 4x aus
$\frac{1}{3} x (x^{2} - 10)$ $=$ $0$
Der Satz vom Nullprodukt besagt, dass ein Produkt immer dann 0 ist, wenn mindestens ein Faktor 0 ist. Der Faktor $\frac{1}{3}$ ist nie 0. Unterscheide deshalb:
$x = 0$ und $x^{2} - 10 = 0$
Der erste Faktor liefert direkt die erste Nullstelle $x_{1} = 0$
Untersuche $x^{2} - 10 = 0$ weiter:
$x^{2} - 10$ $=$ $0$ $+ 10$
$x^{2}$ $=$ $10$
↓
Ziehe die Wurzel. Beachte, dass es zwei Lösungen gibt.
$x_{2}$ $=$ $\sqrt{10} \approx 3,16$
$x_{3}$ $=$ $- \sqrt{10} \approx - 3,16$
Da $x_{3} < - 3$ ist diese Nullstelle nicht in der Definitionsmenge und deshalb nicht weiter interessant.
Bestimme die Art aller Extremstellen, z.B. über die Monotonietabelle:
x
-3
<x<
0
<x<
$\sqrt{10}$
<x<
4,5
$f^{'} (x)$
+
0
-
0
+
$G_{f}$
Rand- TIP (da danach $↗)$
$↗$
HOP
$↘$
TIP
$↗$
Rand- HOP (da davor $↗)$
Bestimme vom Hochpunkt bei $x = 0$ und vom Tiefpunkt bei $x = \sqrt{10}$ die y-Koordinaten durch Einsetzen in f:
$f (0) = \frac{16}{3}$ , also $H O P (0 | \frac{16}{3})$
$f (\sqrt{10}) = - 3$ , also $T I P (\sqrt{10} | - 3)$
und bereits berechnet: $R_{1} (- 3 | - \frac{35}{12})$ und $R_{2} (4,5 | \frac{1105}{192})$
Wertemenge angeben
Wähle nun den kleinsten und den größten y-Wert aller Extrempunkte für die Wertemenge aus.
Als Hilfestellung: $\frac{16}{3} \approx 5,33$ , $- \frac{35}{12} \approx - 2,92$ und $\frac{1105}{192} \approx 5,76$
Der kleinste y-Wert ist also beim Tiefpunkt $T I P (\sqrt{10} | - 3)$ und der größte y-Wert beim Randhochpunkt $R_{2} (4,5 | \frac{1105}{192})$ :
$W_{f} = [- 3; \frac{1105}{192}]$
Beachte aufgrund der eingeschränkten Definitionsmenge auch die Randextrempunkte. Hier sind beide Ränder der Definitionsmenge eingeschlossen, es gibt also zwei Randextrempunkte.
Bestimme die übrigen Extrema wie gewohnt durch:
Ableiten
Nullstellen von $f^{'}$ bestimmen
Nachweis und Art der Extrempunkte über 2. Ableitung, Skizze oder Monotonietabelle
Lage durch Einsetzen in die Ausgangsfunktion f
Die Art der Randextrempunkte kannst du jetzt durch Überlegungen und/oder eine grobe Skizze ebenfalls festlegen.
Die Wertemenge erhältst du, indem du alle y-Koordinaten deiner Extrempunkte betrachtest und den kleinsten und größten Wert als Grenzen der Wertemenge wählst.
Zeichnen Sie unter Verwendung aller bisherigen Ergebnisse den Graphen $G_{f}$ und die Gerade $G_{g}$ in ein kartesisches Koordinatensystem.
Maßstab für beide Achsen: $1 L E = 1 c m$ (5 BE)
Die Zeichnung mit der Wertetabelle ist ein guter Moment, um deine bisher berechneten Ergebnisse zu überprüfen!
Beachte die gegebene Definitions- und die soeben berechnete Wertemenge beim Zeichnen des Koordinatensystems.
Starte zunächst durch die Markierung der Definitionsmenge durch senkrechte, gestrichelte Linien. Zeichne nicht über diese Linien hinaus!
Da du die Funktion zeichnen sollst, fertige eine Wertetabelle für den gegebenen Definitionsbereich an und markiere dann die Punkte.
Gehe anschließend von oben nach unten durch alle Teilaufgaben und markiere berechnete Punkte.
Im ersten Angabentext war auch von der Gerade g die Rede, zeichne diese ebenfalls ein.

x	-3	<x<	0	<x<	$\sqrt{10}$	<x<	4,5
$f^{'} (x)$		+	0	-	0	+
$G_{f}$	Rand- TIP (da danach $↗)$	$↗$	HOP	$↘$	TIP	$↗$	Rand- HOP (da davor $↗)$

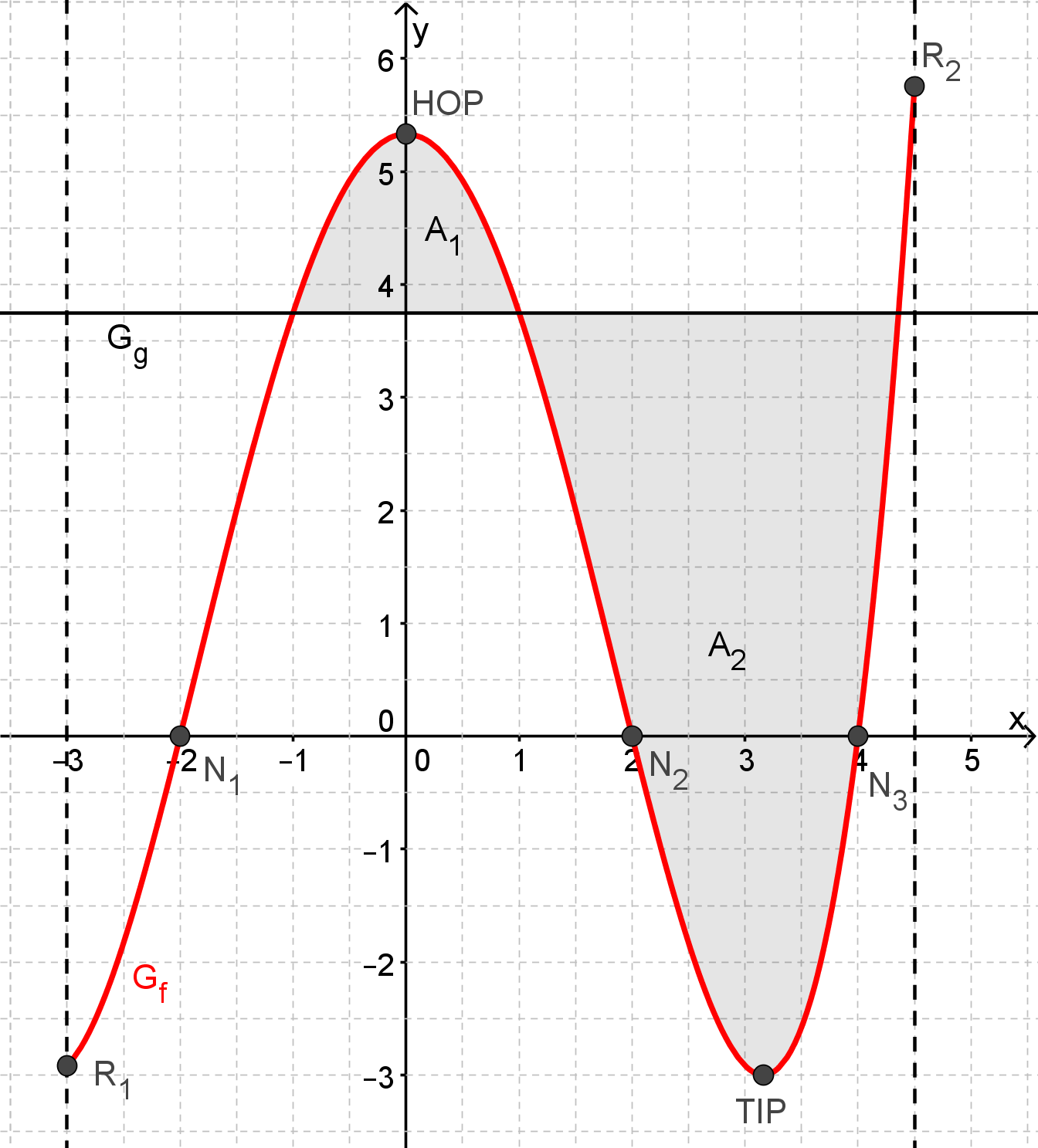
Die Graphen der beiden Funktionen f und g schneiden sich an den Stellen $x_{1} = - 1$ , $x_{2} = 1$ und $x_{3} = \sqrt{19}$ (Nachweis nicht erforderlich) und schließen somit zwei endliche Flächenstücke ein. Berechnen Sie die Maßzahl des Flächeninhalts des kleineren der beiden Flächenstücke. Runden Sie Ihr Ergebnis auf zwei Nachkommastellen. (4 BE)

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das? serlo.org

	$s (x)$
$=$	$f (x) - g (x)$
$=$	$\frac{1}{12} (x^{4} - 20 x^{2} + 64) - \frac{15}{4}$
$=$	$\frac{1}{12} x^{4} - \frac{5}{3} x^{2} + \frac{19}{12}$

$\int_{- 1}^{1} s (x) d x$	$=$	$\int_{- 1}^{1} (\frac{1}{12} x^{4} - \frac{5}{3} x^{2} + \frac{19}{12}) d x$
	↓	Bilde eine Stammfunktion S(x) von s(x)
	$=$	${[\frac{1}{60} x^{5} - \frac{5}{9} x^{3} + \frac{19}{12} x]}_{- 1}^{1}$
	↓	Setze 1 und -1 in diese Stammfunktion ein, subtrahiere die Ergebnisse
	$=$	$S (1) - S (- 1)$
	$=$	$\frac{94}{45}$

Teil 2, Analysis II

Randextrema

Extremstellen bestimmen

Wertemenge angeben

Flächenstück markieren

Differenzfunktion bilden

Wert des bestimmten Integrals berechnen

$f (x)$	$=$	$0$
$\frac{1}{12} (x^{4} - 20 x^{2} + 64)$	$=$	$0$	$: \frac{1}{12}$
	↓	Die $\frac{1}{12}$ haben keinen Einfluss auf die Nullstellen (Satz vom Nullprodukt)
$x^{4} - 20 x^{2} + 64$	$=$	$0$

$u_{1}$	$=$	$4$
	↓	verwende $u = x^{2}$
$x^{2}$	$=$	$4$
	↓	Ziehe die Wurzel. Vergiss nicht, dass es zwei Lösungen gibt!
$x_{1}$	$=$	$2$
$x_{2}$	$=$	$- 2$

$u_{2}$	$=$	$16$
	↓	verwende $u = x_{}^{2}$
$x^{2}$	$=$	$16$
	↓	Ziehe die Wurzel.
$x_{3}$	$=$	$4$
$x_{4}$	$=$	$- 4$

$f^{'} (x)$	$=$	$0$
$\frac{1}{12} (4 x^{3} - 40 x)$	$=$	$0$
	↓	Klammere 4x aus
$\frac{1}{3} x (x^{2} - 10)$	$=$	$0$

$x^{2} - 10$	$=$	$0$	$+ 10$
$x^{2}$	$=$	$10$
	↓	Ziehe die Wurzel. Beachte, dass es zwei Lösungen gibt.
$x_{2}$	$=$	$\sqrt{10} \approx 3,16$
$x_{3}$	$=$	$- \sqrt{10} \approx - 3,16$