Aufgaben zu Spurpunkten einer Geraden

Berechne die möglichen Spurpunkte der gegebenen Geraden.

Skizziere jeweils die Geraden und gib an, welche Lage die Geraden im Koordinatensystem haben.

$g : \vec{X} = (\begin{array}{c} 1 \\ 2 \\ 3 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ 2 \\ 0 \end{array})$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Spurpunkte einer Geraden
Spurpunkte berechnen
Um den Spurpunkt in der $x_{1} x_{2}$ -Ebene zu berechnen, setzt man $x_{3} = 0$ in der Geradengleichung und berechnet den Parameter $r$ :
$x_{3}$ $=$ $3 + r \cdot 0$
↓
Setze $x_{3} = 0$ .
$0$ $=$ $3 + r \cdot 0$
Die erhaltene Gleichung $0 = 3 + r \cdot 0$ ist für kein $r$ erfüllbar (falsche Aussage).
Somit gibt es keinen Spurpunkt in der $x_{1} x_{2}$ -Ebene.
Für die Berechnung des Spurpunktes in der $x_{1} x_{3}$ -Ebene setzt man $x_{2} = 0$ in der Geradengleichung und berechnet den Parameter $r$ .
$x_{2}$ $=$ $2 + 2 \cdot r$
↓
Setze $x_{2} = 0$ .
$0$ $=$ $2 + 2 \cdot r$ $- 2$
↓
Löse nach $r$ auf.
$- 2$ $=$ $2 \cdot r$ $: 2$
$r$ $=$ $- 1$
Der Wert $r = - 1$ wird in die Geradengleichung eingesetzt, um die Koordinaten des Spurpunktes in der $x_{1} x_{3}$ -Ebene zu berechnen:
${\vec{X}}_{S_{13}}$ $=$ $(\begin{array}{c} 1 \\ 2 \\ 3 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ 2 \\ 0 \end{array})$
↓
Setze $r = - 1$ ein.
$=$ $(\begin{array}{c} 1 \\ 2 \\ 3 \end{array}) + (- 1) \cdot (\begin{array}{c} - 1 \\ 2 \\ 0 \end{array})$
↓
Vereinfache
$=$ $(\begin{array}{c} 1 + 1 \\ 2 - 2 \\ 3 - 0 \end{array})$
$=$ $(\begin{array}{c} 2 \\ 0 \\ 3 \end{array})$
Der Spurpunkt in der $x_{1} x_{3}$ -Ebene hat die Koordinaten $S_{13} (2 | 0 | 3)$ .
Für den Spurpunkt in der $x_{2} x_{3}$ -Ebene setzt man $x_{1} = 0$ in der Geradengleichung und berechnet den Parameter $r$ .
$x_{1}$ $=$ $1 - r$
↓
Setze $x_{1} = 0$ .
$0$ $=$ $1 - r$ $+ r$
↓
Löse nach $r$ auf.
$r$ $=$ $1$
Der Wert $r = 1$ wird in die Geradengleichung eingesetzt, um die Koordinaten des Spurpunktes in der $x_{2} x_{3}$ -Ebene zu berechnen:
${\vec{X}}_{S_{23}}$ $=$ $(\begin{array}{c} 1 \\ 2 \\ 3 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ 2 \\ 0 \end{array})$
↓
Setze $r = 1$ ein.
$=$ $(\begin{array}{c} 1 \\ 2 \\ 3 \end{array}) + 1 \cdot (\begin{array}{c} - 1 \\ 2 \\ 0 \end{array})$
$=$ $(\begin{array}{c} 1 - 1 \\ 2 + 2 \\ 3 + 0 \end{array})$
$=$ $(\begin{array}{c} 0 \\ 4 \\ 3 \end{array})$
Der Spurpunkt in der $x_{2} x_{3}$ -Ebene hat die Koordinaten $S_{23} (0 | 4 | 3)$ .
Skizze der Geraden
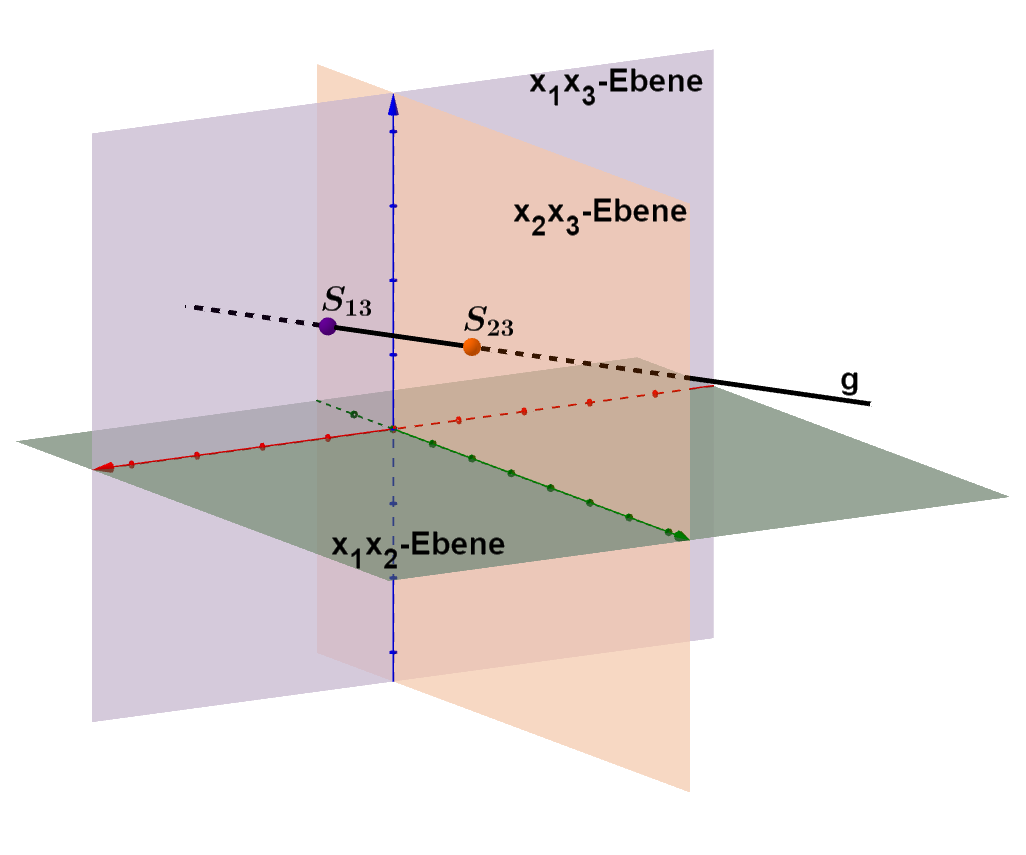
Lage der Geraden im Koordinatensystem
Die Gerade $g$ ist parallel zur $x_{1} x_{2}$ -Ebene.
$h : \vec{O X} = (\begin{array}{c} 1 \\ 2 \\ 1 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 3 \\ - 2 \end{array})$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Spurpunkte einer Geraden
Spurpunkte berechnen
Um den Spurpunkt in der $x_{1} x_{2}$ -Ebene zu berechnen, setzt man $x_{3} = 0$ in der Geradengleichung und berechnet den Parameter $r$ :
$x_{3}$ $=$ $1 - 2 \cdot r$
↓
Setze $x_{3} = 0$ .
$0$ $=$ $1 - 2 \cdot r$ $+ 2 r$
↓
Löse nach $r$ auf.
$2 \cdot r$ $=$ $1$ $: 2$
$r$ $=$ $\frac{1}{2}$
Der Wert $r = \frac{1}{2}$ wird in die Geradengleichung eingesetzt, um die Koordinaten des Spurpunktes in der $x_{1} x_{2}$ -Ebene zu berechnen:
${\vec{X}}_{S_{12}}$ $=$ $(\begin{array}{c} 1 \\ 2 \\ 1 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 3 \\ - 2 \end{array})$
↓
Setze $r = \frac{1}{2}$ ein.
$=$ $(\begin{array}{c} 1 \\ 2 \\ 1 \end{array}) + \frac{1}{2} \cdot (\begin{array}{c} 1 \\ 3 \\ - 2 \end{array})$
↓
Vereinfache
$=$ $(\begin{array}{c} 1 + \frac{1}{2} \\ 2 + \frac{3}{2} \\ 1 - 1 \end{array})$
$=$ $(\begin{array}{c} 1,5 \\ 3,5 \\ 0 \end{array})$
Der Spurpunkt in der $x_{1} x_{2}$ -Ebene hat die Koordinaten $S_{12} (1,5 | 3,5 | 0)$ .
Für die Berechnung des Spurpunktes in der $x_{1} x_{3}$ -Ebene setzt man $x_{2} = 0$ in der Geradengleichung und berechnet den Parameter $r$ .
$x_{2}$ $=$ $2 + 3 \cdot r$
↓
Setze $x_{2} = 0$ .
$0$ $=$ $2 + 3 \cdot r$ $- 2$
↓
Löse nach $r$ auf.
$- 2$ $=$ $3 \cdot r$ $: 3$
$r$ $=$ $- \frac{2}{3}$
Der Wert $r = - \frac{2}{3}$ wird in die Geradengleichung eingesetzt, um die Koordinaten des Spurpunktes in der $x_{1} x_{3}$ -Ebene zu berechnen:
${\vec{X}}_{S_{13}}$ $=$ $(\begin{array}{c} 1 \\ 2 \\ 1 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 3 \\ - 2 \end{array})$
↓
Setze $r = - \frac{2}{3}$ ein.
$=$ $(\begin{array}{c} 1 \\ 2 \\ 1 \end{array}) + (- \frac{2}{3}) \cdot (\begin{array}{c} 1 \\ 3 \\ - 2 \end{array})$
↓
Vereinfache
$=$ $(\begin{array}{c} 1 - \frac{2}{3} \\ 2 - 2 \\ 1 + \frac{4}{3} \end{array})$
$=$ $(\begin{array}{c} \frac{1}{3} \\ 0 \\ \frac{7}{3} \end{array})$
Der Spurpunkt in der $x_{1} x_{3}$ -Ebene hat die Koordinaten $S_{13} (\frac{1}{3} | 0 | \frac{7}{3})$ .
Für den Spurpunkt in der $x_{2} x_{3}$ -Ebene setzt man $x_{1} = 0$ in der Geradengleichung und berechnet den Parameter $r$ .
$x_{1}$ $=$ $1 + r$
↓
Setze $x_{1} = 0$ .
$0$ $=$ $1 + r$ $- 1$
$r$ $=$ $- 1$
Der Wert $r = - 1$ wird in die Geradengleichung eingesetzt, um die Koordinaten des Spurpunktes in der $x_{2} x_{3}$ -Ebene zu berechnen:
${\vec{X}}_{S_{23}}$ $=$ $(\begin{array}{c} 1 \\ 2 \\ 1 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 3 \\ - 2 \end{array})$
↓
Setze $r = - 1$ ein.
$=$ $(\begin{array}{c} 1 \\ 2 \\ 1 \end{array}) + (- 1) \cdot (\begin{array}{c} 1 \\ 3 \\ - 2 \end{array})$
↓
Vereinfache
$=$ $(\begin{array}{c} 1 - 1 \\ 2 - 3 \\ 1 + 2 \end{array})$
$=$ $(\begin{array}{c} 0 \\ - 1 \\ 3 \end{array})$
Der Spurpunkt in der $x_{2} x_{3}$ -Ebene hat die Koordinaten $S_{23} (0 | - 1 | 3)$ .
Skizze der Geraden
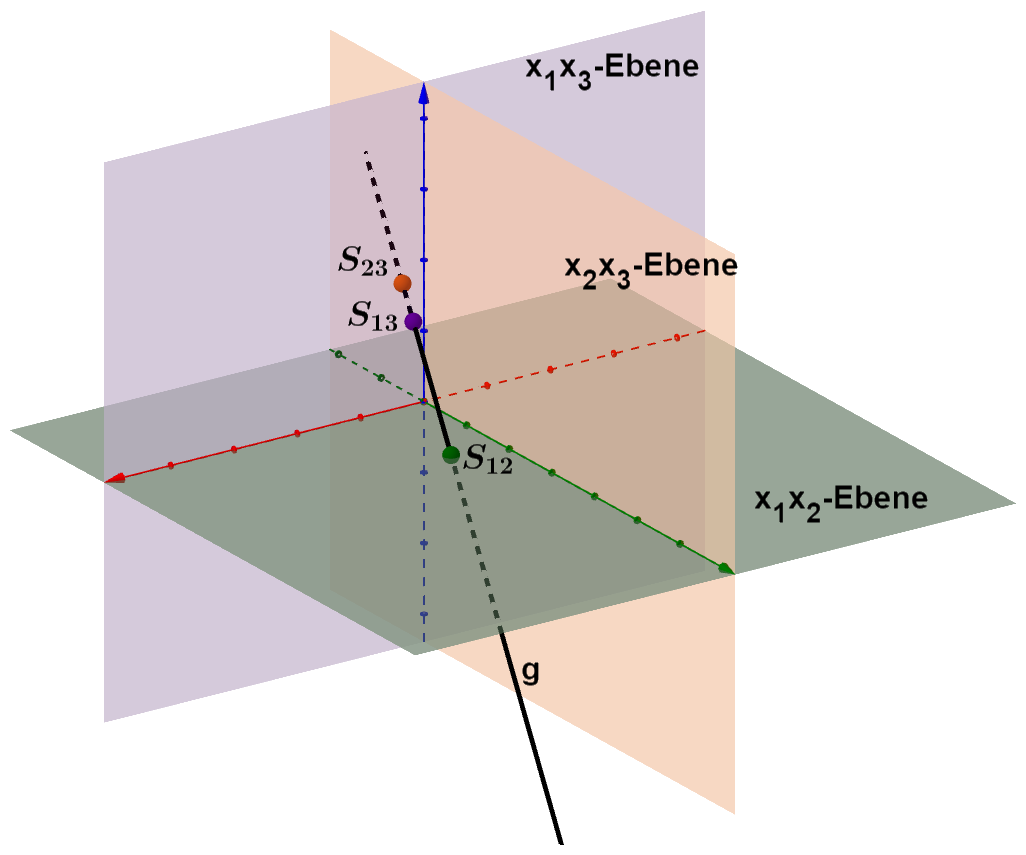
Lage der Geraden im Koordinatensystem
Die Gerade $h$ ist zu keiner Koordinatenebene parallel.
$k : \vec{X} = r \cdot (\begin{array}{c} 2 \\ 2 \\ 1 \end{array})$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Spurpunkte einer Geraden
Anhand der Geradengleichung kannst du feststellen, dass die Gerade $k$ durch den Koordinatenursprung verläuft. Sie ist außerdem zu keiner Koordinatenebene parallel. Es gibt somit nur einen Spurpunkt $S (0 | 0 | 0)$ .
Skizze der Geraden
$l : \vec{X} = (\begin{array}{c} 0 \\ 2 \\ 1 \end{array}) + r \cdot (\begin{array}{c} 0 \\ 3 \\ - 2 \end{array})$

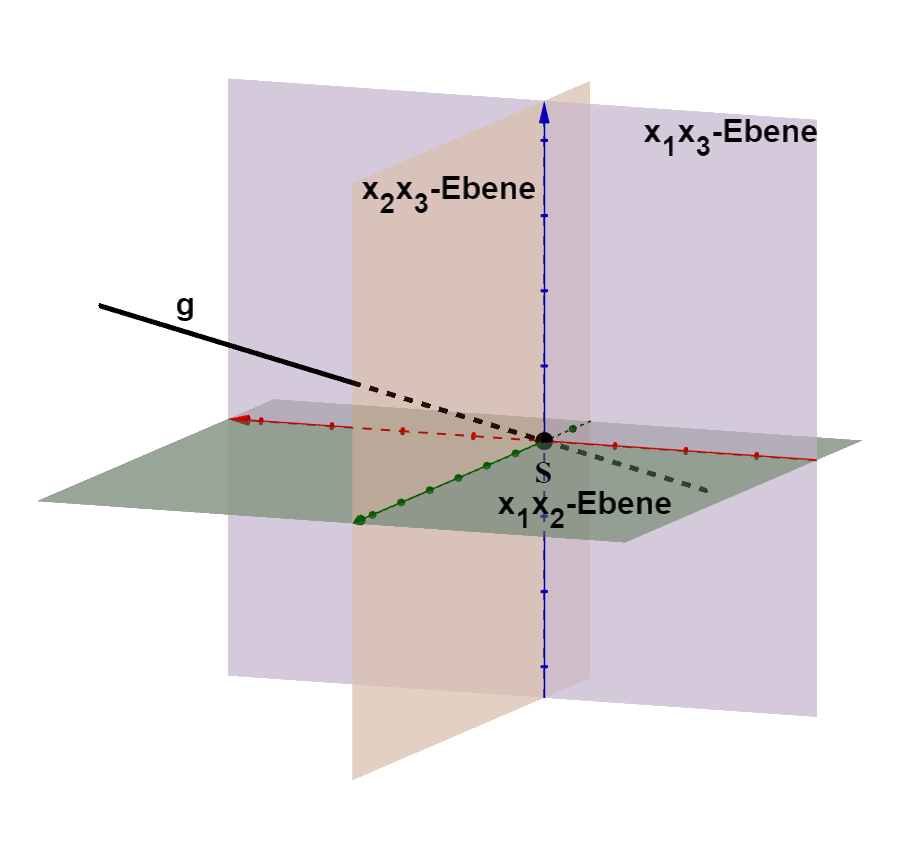
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spurpunkte einer Geraden
Spurpunkte berechnen
Um den Spurpunkt in der $x_{1} x_{2}$ -Ebene zu berechnen, setzt man $x_{3} = 0$ in der Geradengleichung und berechnet den Parameter $r$ :
$x_{3}$ $=$ $1 - 2 \cdot r$
↓
Setze $x_{3} = 0$ .
$0$ $=$ $1 - 2 \cdot r$ $+ 2 r$
$2 \cdot r$ $=$ $1$ $: 2$
$r$ $=$ $\frac{1}{2}$
Der Wert $r = \frac{1}{2}$ wird in die Geradengleichung eingesetzt, um die Koordinaten des Spurpunktes in der $x_{1} x_{2}$ -Ebene zu berechnen:
${\vec{X}}_{S_{12}}$ $=$ $(\begin{array}{c} 0 \\ 2 \\ 1 \end{array}) + r \cdot (\begin{array}{c} 0 \\ 3 \\ - 2 \end{array})$
↓
Setze $r = \frac{1}{2}$ ein.
$=$ $(\begin{array}{c} 0 \\ 2 \\ 1 \end{array}) + (\frac{1}{2}) \cdot (\begin{array}{c} 0 \\ 3 \\ - 2 \end{array})$
↓
Fasse zusammen.
$=$ $(\begin{array}{c} 0 + 0 \\ 2 + \frac{3}{2} \\ 1 - 1 \end{array})$
$=$ $(\begin{array}{c} 0 \\ 3,5 \\ 0 \end{array})$
Der Spurpunkt in der $x_{1} x_{2}$ -Ebene hat die Koordinaten $S_{12} (0 | 3,5 | 0)$ .
Für die Berechnung des Spurpunktes in der $x_{1} x_{3}$ -Ebene setzt man $x_{2} = 0$ in der Geradengleichung und berechnet den Parameter $r$ .
$x_{2}$ $=$ $2 + 3 \cdot r$
↓
Setze $x_{2} = 0$ .
$0$ $=$ $2 + 3 \cdot r$ $- 2$
↓
Löse nach $r$ auf.
$- 2$ $=$ $3 \cdot r$ $: 3$
$r$ $=$ $- \frac{2}{3}$
Der Wert $r = - \frac{2}{3}$ wird in die Geradengleichung eingesetzt, um die Koordinaten des Spurpunktes in der $x_{1} x_{3}$ -Ebene zu berechnen:
${\vec{X}}_{S_{12}}$ $=$ $(\begin{array}{c} 0 \\ 2 \\ 1 \end{array}) + r \cdot (\begin{array}{c} 0 \\ 3 \\ - 2 \end{array})$
↓
Setze $r = - \frac{2}{3}$ ein.
$=$ $(\begin{array}{c} 0 \\ 2 \\ 1 \end{array}) + (- \frac{2}{3}) \cdot (\begin{array}{c} 0 \\ 3 \\ - 2 \end{array})$
↓
Fasse zusammen.
$=$ $(\begin{array}{c} 0 + 0 \\ 2 - 2 \\ 1 + \frac{4}{3} \end{array})$
$=$ $(\begin{array}{c} 0 \\ 0 \\ \frac{7}{3} \end{array})$
Der Spurpunkt in der $x_{1} x_{3}$ -Ebene hat die Koordinaten $S_{13} (0 | 0 | \frac{7}{3})$ .
Für den Spurpunkt in der $x_{2} x_{3}$ -Ebene setzt man $x_{1} = 0$ in der Geradengleichung und berechnet den Parameter $r$ .
$x_{1}$ $=$ $0 + 0 \cdot r$
↓
Setze $x_{1} = 0$ .
$0$ $=$ $0 + 0 \cdot r$
Du hast die Gleichung $0 = 0 + 0 \cdot r$ erhalten. Diese Gleichung ist für alle $r$ erfüllt ( wahre Aussage). Die Gerade hat somit unendlich viele Schnittpunkte mit der $x_{2} x_{3}$ -Ebene, d.h. die Gerade hat auch unendlich viele Spurpunkte in der $x_{2} x_{3}$ -Ebene.
Skizze der Geraden
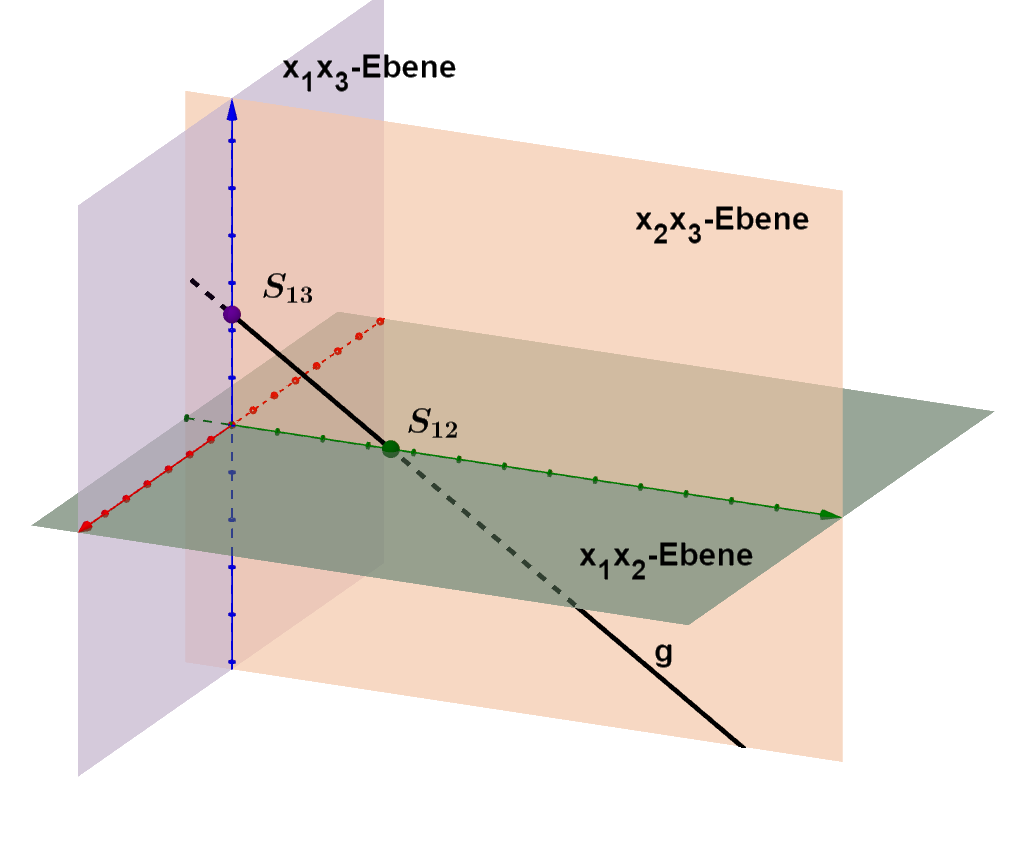
Lage der Geraden im Koordinatensystem
Die Gerade $l$ liegt in der $x_{2} x_{3}$ -Ebene.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org

$x_{3}$	$=$	$3 + r \cdot 0$
	↓	Setze $x_{3} = 0$ .
$0$	$=$	$3 + r \cdot 0$

$x_{2}$	$=$	$2 + 2 \cdot r$
	↓	Setze $x_{2} = 0$ .
$0$	$=$	$2 + 2 \cdot r$	$- 2$
	↓	Löse nach $r$ auf.
$- 2$	$=$	$2 \cdot r$	$: 2$
$r$	$=$	$- 1$

${\vec{X}}_{S_{13}}$	$=$	$(\begin{array}{c} 1 \\ 2 \\ 3 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ 2 \\ 0 \end{array})$
	↓	Setze $r = - 1$ ein.
	$=$	$(\begin{array}{c} 1 \\ 2 \\ 3 \end{array}) + (- 1) \cdot (\begin{array}{c} - 1 \\ 2 \\ 0 \end{array})$
	↓	Vereinfache
	$=$	$(\begin{array}{c} 1 + 1 \\ 2 - 2 \\ 3 - 0 \end{array})$
	$=$	$(\begin{array}{c} 2 \\ 0 \\ 3 \end{array})$

$x_{1}$	$=$	$1 - r$
	↓	Setze $x_{1} = 0$ .
$0$	$=$	$1 - r$	$+ r$
	↓	Löse nach $r$ auf.
$r$	$=$	$1$

${\vec{X}}_{S_{23}}$	$=$	$(\begin{array}{c} 1 \\ 2 \\ 3 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ 2 \\ 0 \end{array})$
	↓	Setze $r = 1$ ein.
	$=$	$(\begin{array}{c} 1 \\ 2 \\ 3 \end{array}) + 1 \cdot (\begin{array}{c} - 1 \\ 2 \\ 0 \end{array})$
	$=$	$(\begin{array}{c} 1 - 1 \\ 2 + 2 \\ 3 + 0 \end{array})$
	$=$	$(\begin{array}{c} 0 \\ 4 \\ 3 \end{array})$

$x_{3}$	$=$	$1 - 2 \cdot r$
	↓	Setze $x_{3} = 0$ .
$0$	$=$	$1 - 2 \cdot r$	$+ 2 r$
	↓	Löse nach $r$ auf.
$2 \cdot r$	$=$	$1$	$: 2$
$r$	$=$	$\frac{1}{2}$

${\vec{X}}_{S_{12}}$	$=$	$(\begin{array}{c} 1 \\ 2 \\ 1 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 3 \\ - 2 \end{array})$
	↓	Setze $r = \frac{1}{2}$ ein.
	$=$	$(\begin{array}{c} 1 \\ 2 \\ 1 \end{array}) + \frac{1}{2} \cdot (\begin{array}{c} 1 \\ 3 \\ - 2 \end{array})$
	↓	Vereinfache
	$=$	$(\begin{array}{c} 1 + \frac{1}{2} \\ 2 + \frac{3}{2} \\ 1 - 1 \end{array})$
	$=$	$(\begin{array}{c} 1,5 \\ 3,5 \\ 0 \end{array})$

$x_{2}$	$=$	$2 + 3 \cdot r$
	↓	Setze $x_{2} = 0$ .
$0$	$=$	$2 + 3 \cdot r$	$- 2$
	↓	Löse nach $r$ auf.
$- 2$	$=$	$3 \cdot r$	$: 3$
$r$	$=$	$- \frac{2}{3}$

${\vec{X}}_{S_{13}}$	$=$	$(\begin{array}{c} 1 \\ 2 \\ 1 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 3 \\ - 2 \end{array})$
	↓	Setze $r = - \frac{2}{3}$ ein.
	$=$	$(\begin{array}{c} 1 \\ 2 \\ 1 \end{array}) + (- \frac{2}{3}) \cdot (\begin{array}{c} 1 \\ 3 \\ - 2 \end{array})$
	↓	Vereinfache
	$=$	$(\begin{array}{c} 1 - \frac{2}{3} \\ 2 - 2 \\ 1 + \frac{4}{3} \end{array})$
	$=$	$(\begin{array}{c} \frac{1}{3} \\ 0 \\ \frac{7}{3} \end{array})$

$x_{1}$	$=$	$1 + r$
	↓	Setze $x_{1} = 0$ .
$0$	$=$	$1 + r$	$- 1$
$r$	$=$	$- 1$

${\vec{X}}_{S_{12}}$	$=$	$(\begin{array}{c} 0 \\ 2 \\ 1 \end{array}) + r \cdot (\begin{array}{c} 0 \\ 3 \\ - 2 \end{array})$
	↓	Setze $r = \frac{1}{2}$ ein.
	$=$	$(\begin{array}{c} 0 \\ 2 \\ 1 \end{array}) + (\frac{1}{2}) \cdot (\begin{array}{c} 0 \\ 3 \\ - 2 \end{array})$
	↓	Fasse zusammen.
	$=$	$(\begin{array}{c} 0 + 0 \\ 2 + \frac{3}{2} \\ 1 - 1 \end{array})$
	$=$	$(\begin{array}{c} 0 \\ 3,5 \\ 0 \end{array})$

$x_{1}$	$=$	$0 + 0 \cdot r$
	↓	Setze $x_{1} = 0$ .
$0$	$=$	$0 + 0 \cdot r$

Aufgaben zu Spurpunkten einer Geraden

Spurpunkte berechnen

Skizze der Geraden

Lage der Geraden im Koordinatensystem

Spurpunkte berechnen

Skizze der Geraden

Lage der Geraden im Koordinatensystem

Skizze der Geraden

Spurpunkte berechnen

Skizze der Geraden

Lage der Geraden im Koordinatensystem