A I

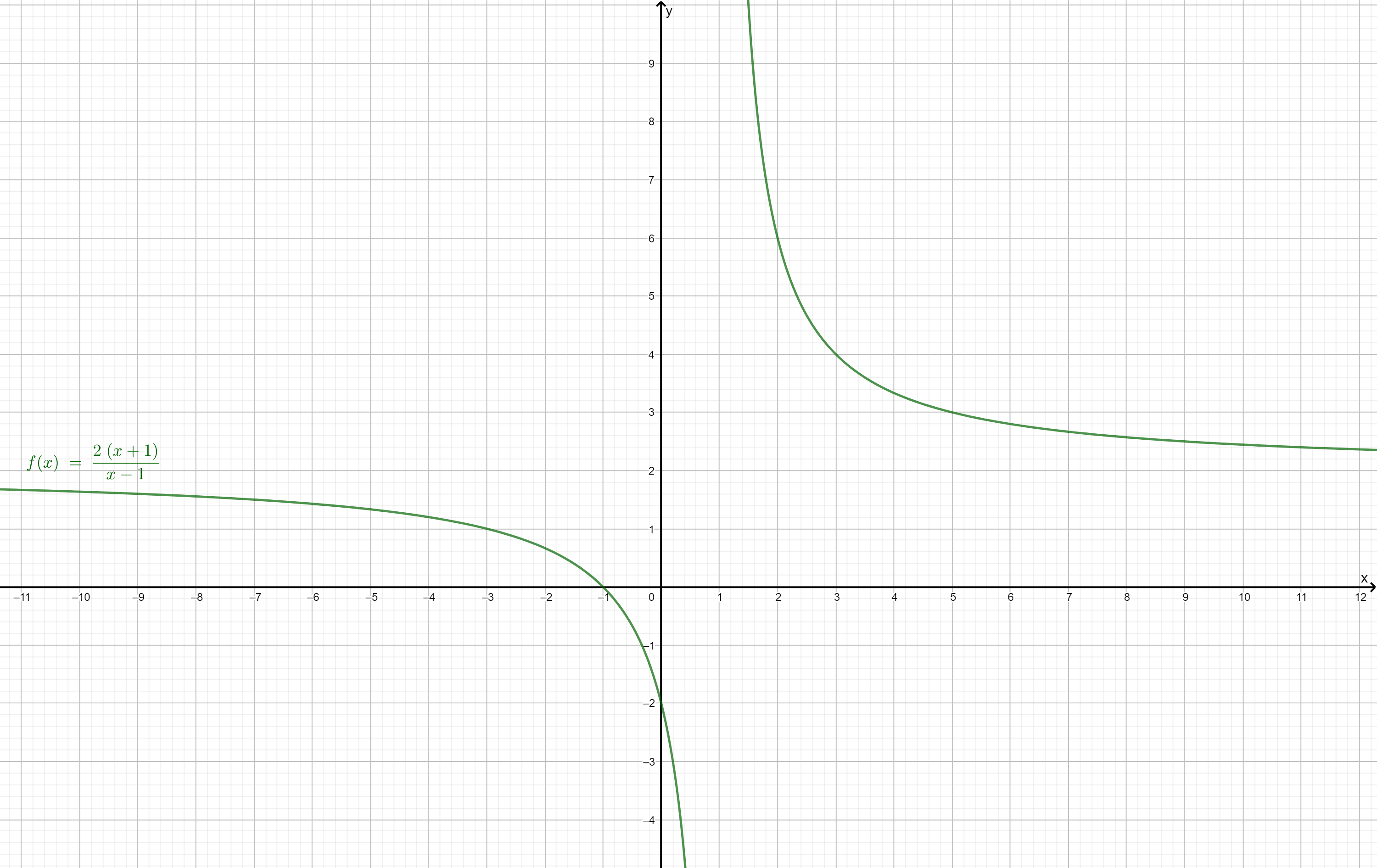
Gegeben ist die Funktion $g : x \mapsto \frac{2 (x + 1)^{2}}{x^{2} - 1}$ mit der maximalen Definitionsmenge $D_{g} \subset ℝ$ .

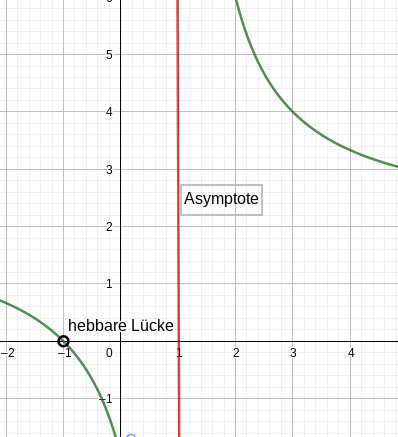
Geben Sie $D_{g}$ an, prüfen Sie $g$ auf Nullstellen und folgern Sie daraus die Art der Definitionslücken. Untersuchen Sie das Verhalten der Funktionswerte bei Annäherung an die Definitionslücken. (7 BE)

Definitionsmenge
Die Definitionsmenge einer Funktion gibt an, welche Zahlen man für $x$ einsetzen kann, damit die Funktion definiert ist.
Hier darf der Nenner nicht $0$ sein. Also setzt man den Nenner gleich $0$ um zu sehen für welche Zahlen die Funktion nicht definiert ist:
$x^{2} - 1 = 0$ | $+ 1$
$x^{2} = 1$ | $\sqrt{}$
$\Rightarrow x_{1} = 1$
$\Rightarrow x_{2} = - 1$
$D_{g} = ℝ \ {- 1; 1}$
Einfacher berechnet man das mit dem Satz vom Nullprodukt:
$x^{2} - 1 = (x - 1) \cdot (x + 1) = 0$
$⟺ x - 1 = 0 \lor x + 1 = 0$
$⟺ x = 1 \lor x = - 1$
Nullstellen
Um die Nullstellen dieser Funktion zu bestimmen, muss man den Zähler gleich $0$ setzen:
$2 (x + 1)^{2} = 0$
$⟺ 2 (x^{2} + 2 x + 1) = 0$
$⟺ 2 \cdot x^{2} + 2 \cdot 2 x + 2 \cdot 1 = 0$
$⟺ 2 x^{2} + 4 x + 2 = 0$
Lösung mit der Mitternachtsformel
$x_{1,2} = \frac{- 4 \pm \sqrt{4^{2} - 4 \cdot 2 \cdot 2}}{2 \cdot 2}$
$x_{1,2} = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
$x_{1,2} = \frac{- 4 \pm \sqrt{16 - 16}}{4}$
$x_{1,2} = \frac{- 4 \pm \sqrt{0}}{4}$
$x_{1,2} = \frac{- 4 \pm \sqrt{0}}{4}$
$x = - 1$
Lösung mit dem Satz vom Nullprodukt
"Ein Produkt ist $0$ , wenn einer der beiden Faktoren $0$ ist."
Also muss in diesem Fall nur $(x + 1)^{2}$ oder einfacher nur $(x + 1)$ gleich $0$ sein.
$x + 1 = 0$ | $- 1$
$x = - 1$
$x = - 1$ ist eine hebbare Lücke, weil hier der Zähler eine Nullstelle hat, wobei die Ordnung (2, es ist ja eine doppelte Nullstelle) größer oder gleich der Ordnung der Nullstelle des Nenners (1, es ist eine einfache Nullstelle) ist.
Bei $x = 1$ gibt es eine senkrechte Asymptote, weil es nur eine Definitionslücke ist.
Das Verhalten an Definitionslücken berechnet man mit dem Limes
von links:
$\lim_{x \to 1^{-}} g (x) = \lim_{x \to 1^{-}} \frac{2 (x + 1)^{2}}{x^{2} - 1} = \lim_{x \to 1^{-}} \frac{2 (x + 1)^{2}}{(x + 1) (x - 1)} = \lim_{x \to 1^{-}} \frac{2 (x + 1)}{x - 1}$
Beim Grenzwert von rechts ändert sich nur das Vorzeichen des Nenners, also ist der Grenzwert $+ \infty .$
Alternativ kann man argumentieren, dass es wegen der einfachen Nullstelle des Nenners eine Polstelle mit Vorzeichenwechsel ist.
Die Funktion $f : x \mapsto \frac{2 (x + 1)}{x - 1}$ mit $D_{f} = ℝ ∖ {1}$ ist die stetige Fortsetzung der Funktion $g$ (Nachweis nicht erforderlich). Ihr Graph wird mit $G_{f}$ bezeichnet.
Geben Sie Art und Gleichungen aller Asymptoten von $G_{f}$ an und untersuchen Sie, ob sich der Graph der Funktion $f$ für $x \to + \infty$ der Asymptote von oben oder unten nähert. (5 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionslücken
Senkrechte Asymptote
$x - 1$ $=$ $0$ $+ 1$
$x$ $=$ $1$
=> Senkrechte Asymptote bei x =1.
Waagerechte Asymptote
Es gibt eine waagerechte Asymptote bei y=2.
Begründung:
Wenn Zählergrad = Nennergrad dann gilt, dass die Faktoren vor dem höchsten Grad die horizontale Asymptote ergeben.
Faktor vor dem höchsten Grad im Zähler ist 2. Faktor vor dem höchsten Grad im Nenner ist 1 => $\frac{2}{1} = 2$ .
Die waagerechte Asymptote lautet demnach y = 2.
Eine Senkrechte Asymptote ist dort, wo die Funktion ihre Definitionslücke hat. Dazu muss der Nenner gleich 0 gesetzt werden.
Für die waagerechte Asympotte muss Zählergrad und Nennergrad betrachtet werden.
Ermitteln Sie die maximalen Monotonieintervalle von f und geben Sie die Wertemenge von f an. (4 BE)
$[mögliches Teilergebnis: f^{'} (x) = - \frac{4}{(x - 1)^{2}}]$
Zeichnen Sie $G_{f}$ und seine Asymptoten unter Berücksichtigung der bisherigen Ergebnisse für $- 4 \leq x \leq 6$ in ein kartesisches Koordinatensystem. (4 BE)
Der Graph $G_{f}$ , die $y$ -Achse und die Geraden $y = 2$ und $x = a$ mit dem reellen Parameter $a < – 1$ begrenzen ein Flächenstück A. Kennzeichnen Sie diese Fläche für $a = – 3$ im Koordinatensystem von Teilaufgabe e) und berechnen Sie deren Flächenmaßzahl $A (a)$ in Abhängigkeit von $a$ . (5 BE)
[mögliches Ergebnis: $A (a) = 4 \ln (1 - a)$ ]
Untersuchen Sie, ob $A (a)$ für $a \mapsto - \infty$ einen endlichen Wert annimmt. (2 BE)
Die Funktion $F$ ist eine Stammfunktion der Funktion $f .$ Geben Sie nur mit den bisherigen Ergebnissen die maximalen Monotonieintervalle des Graphen der Funktion $F$ für $x < 1$ an.