Seitenhalbierende
Die Seitenhalbierenden eines Dreiecks sind Geraden, die von einem Eckpunkt des Dreiecks durch den Mittelpunkt der gegenüberliegenden Seite gehen.
In jedem Dreieck schneiden sich die drei Seitenhalbierenden in einem Punkt, dem Schwerpunkt.
Konstruktion
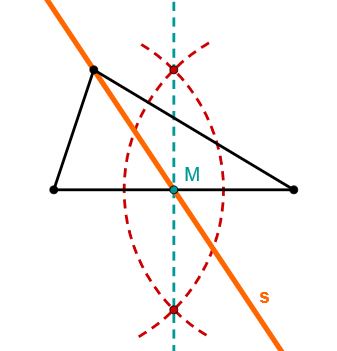
Man konstruiert zwei Hilfskreise, die ihre Mittelpunkte in den Endpunkten einer Dreiecksseite haben. Die Radien der Kreise müssen gleich groß und länger als die Hälfte der Dreiecksseite sein.
Nun verbindet man die beiden Schnittpunkte der Kreise, um die Mittelsenkrechte zu erhalten.
Der Schnittpunkt der Mittelsenkrechten und der gegenüberliegende Eckpunkt bestimmen die Seitenhalbierende.
Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unsererDatenschutzerklärung.
Video
Laden
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
