Nachtermin Teil A

Nebenstehende Skizze zeigt den Axialschnitt eines Rotationskörpers, der das Glas einer Sanduhr darstellt.

Es gilt: $M C = M E = M D = r = 10 mm; A G = 2 mm; ∢ F B A = 59 °; [B C] ‖ [E F]; [A G] ‖ [B F]$

Die beiden Hälften des Glases sind jeweils $50 mm$ hoch. Die untere Hälfte ist bis zur Fülllinie $B F$ mit Sand gefüllt.

Wird die Sanduhr umgedreht, rieseln pro Sekunde durchschnittlich $50 {mm}^{3}$ des Sandes von der oberen in die untere Hälfte des Glases. Berechnen Sie, nach welcher Zeit sich der Sand wieder vollständig in der unteren Hälfte des Glases befindet.

Runden Sie auf Ganze.

$[$ Teilergebnis: $B C = 25 mm$ $]$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumen zusammengesetzter Körper

Um das Volumen des Sands in der Sanduhr zu bestimmen, müssen wir das Volumen des Sands in der unteren Halbkugel mit dem Volumen des Sands im Zylinder addieren.

\begin{array}{rcl} V_{S a n d} & = & V_{H a l b k u g e l} + V_{Z y l i n d e r} \\ = & \frac{1}{2} V_{K u g e l} + V_{Z y l i n d e r} \end{array}

Um $V_{K u g e l}$ zu bestimmen, benutzt du die Formel für das Kugelvolumen, also

V_{K u g e l} = \frac{4}{3} π r^{3} = \frac{4}{3} \cdot π \cdot (10 mm)^{3}

Jetzt fehlt nur noch das Volumen des mit Sand gefüllten Zylinders. Das wird ein wenig schwieriger.

Das Volumen eines Zylinders bestimmt man über die Formel

V_{Z y l i n d e r} = π r^{2} h

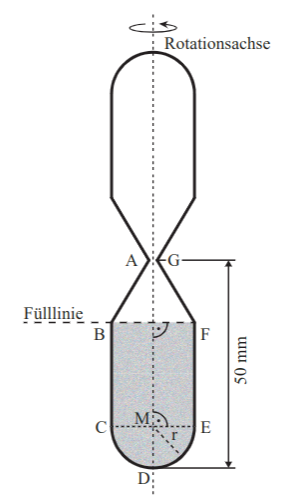
Die Höhe des Zylinders ist jedoch nicht angegeben und muss über andere Angaben aus der Aufgabenstellung ermittelt werden. Eine Skizze hilft dir oft, klarer zu sehen, was gegeben ist und was nicht.

Da die Höhe der unteren Sanduhrhälfte angegeben ist, können wir $h$ bestimmen, indem wir die Höhe des oberen Kegelstumpfs $k$ berechnen.

$50 mm = D M + h + k$

$D M$ ist wiederrum gegeben, aber wir müssen noch ein wenig rechnen, um $k$ zu bestimmen.

Bestimmung von k

Aus der Angabe kannst du rauslesen, dass $A G = 2 mm$ und $∢ F B A = 59 °$ .

Durch diese Angaben lässt sich ein rechtwinkliges Dreieck zeichnen.

Die Länge $A G$ ist angegeben. Um die untere Seitenlänge des Dreiecks zu bestimmen und $[A G] | | [B F]$ ist, ist die Seitenlänge $r - 1 mm = 10 mm - 1 mm = 9 mm$ .

Mit dem Tangens kannst du dann $k$ bestimmen:

\begin{array}{lrcl} \tan (59 °) & = & \frac{k}{9 mm} \\ \Leftrightarrow & k & = & \tan (59 °) \cdot 9 mm \\ \Leftrightarrow & k & \approx & 15 mm \end{array}

Das Schlimmste ist nun geschafft!

Berechnung von $h$

Jetzt kannst du die Formel von oben nutzen, um $h$ zu bestimmen.

$50 mm = M D + h + k = r + h + k$

$r$ und $k$ kennst du mittlerweile. So ergibt sich für $h$ :

$h = 50 mm - r - k = 50 mm - 10 mm - 15 mm = 25 mm$

Berechnung des Zylindervolumens

Jetzt, wo du $h$ bestimmt hast, kannst du das Zylindervolumen endlich berechnen. Setze dafür $h$ in die Formel von oben ein:

$V_{Z y l i n d e r} = π r^{2} h_{} = π \cdot (10 mm)^{2} \cdot 25 mm$

Bestimmung des Volumens des Sands in der Sanduhr

Nun kannst du die Volumen des Sands im Zylinder und der Halbkugel addieren und bekommst das Volumen des Sands in der Sanduhr:

$\begin{array}{rcl} V_{S a n d} & = & \frac{1}{2} V_{K u g e l} + V_{Z y l i n d e r} \\ = & (\frac{1}{2} \cdot \frac{4}{3} \cdot π \cdot 10^{3} + π \cdot 10^{2} \cdot 25) {mm}^{3} \\ = & 9948 {mm}^{3} \end{array}$

(auf Ganze gerundet)

Bestimmung der Zeit bis der Sand durchläuft

Pro Minute laufen $50 {mm}^{3}$ Sand von einer Seite der Sanduhr auf die andere. Somit braucht es $\frac{9948 {mm}^{3}}{50 \frac{{mm}^{3}}{s}} \approx 199 s$ bis der Sand durchgelaufen ist.

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das? serlo.org