Teil B, Gruppe 3

Der Flächeninhalt des hellgrauen Dreiecks beträgt 144 cm².Berechne den Flächeninhalt und den Umfang des dunkelgrauen Quadrats. (4 Punkte)

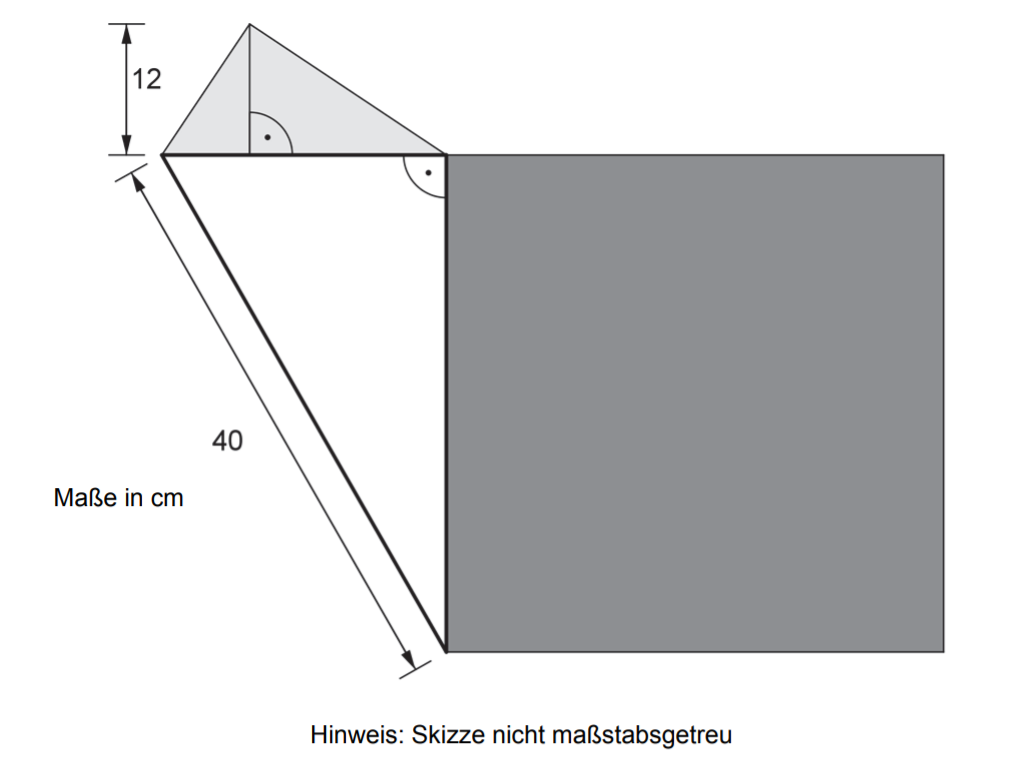
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadrat

Bestimmung des Flächeninhalts und Umfangs eines Quadrates.

Thema dieser Aufgabe ist der Flächeninhalt und Umfang eines Quadrats. In dieser Aufgabe werden aber auch der Flächeninhalt eines Dreiecks und der Satz des Pythagoras gebraucht.

Gegeben:

Flächeninhalt des hellgrauen Dreiecks: $A_{D r e i e c k} = 144 [c m^{2}]$
Aus der Skizze: Höhe des hellgrauen Dreiecks $h = 12 [c m]$
Aus der Skizze: Seitenlänge eines der Seiten des weißen Dreiecks $b = 40 [c m]$

Gesucht: Flächeninhalt und Umfang des dunkelgrauen Quadrats

Vorüberlegung

Um den Flächeninhalt und den Umfang des Quadrats zu berechnen, musst du zunächst die Seitenlänge $a$ des Quadrats bestimmen.

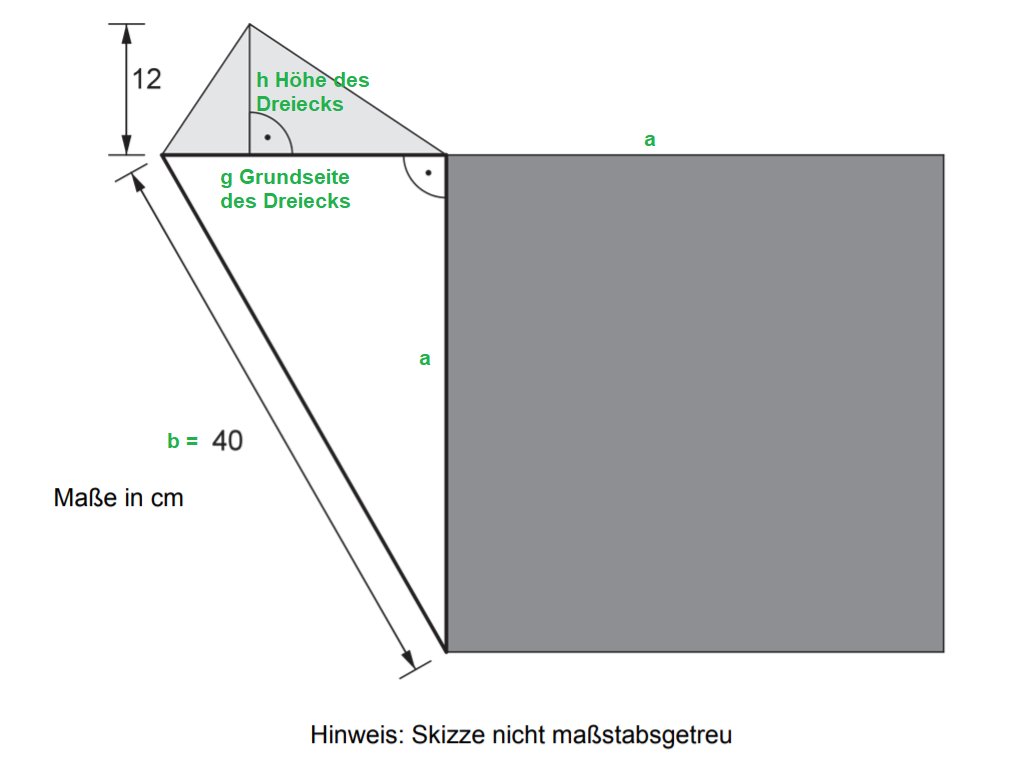
Um $a$ wiederum zu bestimmen, kannst du das weiße Dreieck benutzen. In diesem rechtwinkligen Dreieck ist die Seitenlänge $b$ gegeben, aber $g$ wiederum nicht.

$g$ kann jedoch bestimmt werden, wenn du das hellgraue Dreieck genauer betrachtest (siehe obige Skizze).

Die Grundseite g des hellgrauen Dreiecks bestimmen

Berechne $g$ , indem du den Flächeninhalt des hellgrauen Dreiecks $A_{D r e i e c k}$ und dessen Höhe $h$ verwendest (siehe obige Skizze).

Die Formel für den Flächeninhalt lautet:

$A_{D r e i e c k} = \frac{1}{2} \cdot g \cdot h$

Multipliziere mit 2.

Dividiere durch h.

$\Rightarrow g = \frac{2 \cdot A_{D r e i e c k}}{h} = \frac{2 \cdot 144 c m^{2}}{12 c m} = \frac{2 \cdot 12 \cdot 12 c m^{2}}{12 c m}$

Kürze durch $12 c m$ .

$\Rightarrow g = 2 \cdot 12 c m = 24 c m$

(Alternativ kannst du auch A = 144 und h = 12 sofort einsetzen und dann g berechnen. Das geht etwas einfacher.)

Die Seite a des Quadrats bestimmen

Um $a$ zu bestimmen, benutze das weiße Dreieck. In diesem Dreieck sind nämlich die Seitenlängen $b$ und $g$ nun gegeben, und du kannst die Seitenlänge $a$ mit Hilfe des Satzes des Pythagoras berechnen (siehe obige Skizze):

$b^{2} = a^{2} + g^{2}$

Nun setze die Längen für b und $g$ ein.

$(40 c m)^{2} = a^{2} + (24 c m)^{2}$ I $- (24 c m)^{2}$

$a^{2} = (40 c m)^{2} - (24 c m)^{2}$

Berechne die Quadrate.

$a^{2} = 1600 c m^{2} - 576 c m^{2}$

Fasse zusammen.

$a^{2} = 1024 c m^{2}$

(Das ist bereits der Flächeninhalt des Quadrats. Er wird unten nur zur Sicherheit noch einmal ausführlich berechnet.)

Ziehe die Wurzel.

$a_{1,2} = \pm \sqrt{1024 c m^{2}}$

Da $a$ eine Länge ist, ist nur die positive Lösung sinnvoll.

$a = \sqrt{1024 c m^{2}} = \sqrt{32 \cdot 32 c m^{2}} = 32 c m$

Den Flächeninhalt des Quadrats bestimmen

Der Flächeninhalt eines Quadrats berechnet sich wie folgt:

$A_{Q u a d r a t} = a \cdot a = 32 c m \cdot 32 c m = 1024 c m^{2}$

Den Umfang des Quadrats bestimmen

Der Umfang eines Quadrats berechnet sich wie folgt:

$U_{Q u a d r a t} = a + a + a + a = 4 \cdot a = 4 \cdot 32 c m = 128 c m$

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das? serlo.org