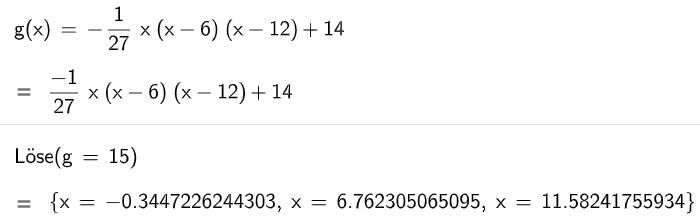B2

1
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 1
Gegeben ist die in $ℝ$ definierte Funktion $f$ mit $f (x) = \frac{1}{27} x^{3} - \frac{4}{3} x$ . Ihr Graph $G_{f}$ hat den Wendepunkt $(0 | 0)$ .
Begründen Sie, dass $G_{f}$ symmetrisch bezüglich seines Wendepunktes ist.
Bestimmen Sie die Koordinaten der Schnittpunkte von $G_{f}$ mit den Koordinatenachsen.
(1 P + 2 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Begründe, dass $G_{f}$ symmetrisch bezüglich seines Wendepunktes ist
Die Funktion $f$ ist ganzrational und hat nur ungerade Exponenten, deshalb ist $G_{f}$ symmetrisch bezüglich seines Wendepunktes $(0 | 0)$ .
Bestimme die Koordinaten der Schnittpunkte von $G_{f}$ mit den Koordinatenachsen
Löse die Gleichung $f (x) = 0 \Rightarrow x = - 6 \lor x = 0 \lor x = 6$
Damit ergeben sich die Schnittpunkte $(- 6 | 0), (0 | 0)$ und $(6 | 0)$ mit den Koordinatenachsen.
Teil 1
Die Funktion $f$ ist ganzrational und hat nur ungerade Exponenten. Was folgt daraus?
Teil 2
Löse die Gleichung $f (x) = 0$ .

Für jedes $b \in ℝ, b > 0$ , gilt $\int_{- b}^{b} f (x) d x = 0$ .
Erklären Sie dieses Ergebnis. (2 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Erkläre das Ergebnis
Es ist $\int_{- b}^{b} f (x) d x = 0$ .
Aufgrund der Punktsymmetrie von $G_{f}$ zum Ursprung existiert zu jedem Flächenstück, das im Intervall $[- b; 0]$ zwischen $G_{f}$ und der $x$ -Achse liegt, ein gleich großes Flächenstück, das im Intervall $[0; b]$ zwischen $G_{f}$ und der $x$ -Achse liegt und sich auf der entgegengesetzten Seite der $x$ -Achse befindet. Diese orientierten Flächeninhalte heben sich gegeneinander auf.
Beachte die Punktsymmetrie bezüglich des Koordinatenursprungs.

$G_{f}$ hat zwei Extrempunkte.
Zeigen Sie, dass einer der beiden ein Tiefpunkt mit der $x$ -Koordinate $\sqrt{12}$ ist. (3 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremum
Zeige, dass einer der beiden ein Tiefpunkt mit der $x$ -Koordinate $\sqrt{12}$ ist
Bekannt ist, dass $G_{f}$ zwei Extrempunkte hat.
Wenn der Tiefpunkt die $x$ -Koordinate $\sqrt{12}$ hat, dann muss $f^{'} (\sqrt{12}) = 0$ und $f^{''} (\sqrt{12}) > 0$ sein.
Berechne $f^{'} (x) = \frac{1}{9} x^{2} - \frac{4}{3}$ und $f^{''} (x) = \frac{2}{9} x$ .
Dann gilt:
$f^{'} (\sqrt{12}) = \frac{1}{9} {(\sqrt{12})}^{2} - \frac{4}{3} = \frac{12}{9} - \frac{4}{3} = 0$ und $f^{''} (\sqrt{12}) = \frac{2}{9} \cdot \sqrt{12} > 0$
Folglich ist bestätigt, dass ein Tiefpunkt mit der $x$ -Koordinate $\sqrt{12}$ existiert.
Wenn der Tiefpunkt die $x$ -Koordinate $\sqrt{12}$ hat, dann muss $f^{'} (\sqrt{12}) = 0$ und $f^{''} (\sqrt{12}) > 0$ sein.
Überprüfe die beiden Bedingungen.

Bestimmen Sie eine Gleichung der Tangente t an $G_{f}$ im Punkt $P (6 | f (6))$ .
[Zur Kontrolle: $t : y = \frac{8}{3} x - 16.]$ (3 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
Bestimme eine Gleichung der Tangente t an $G_{f}$ im Punkt $P (6 | f (6))$
Die allgemeine Tangentengleichung lautet $t : y = m \cdot x + b$ .
$m = f^{'} (6) = f^{'} (6) = \frac{1}{9} \cdot 6^{2} - \frac{4}{3} = \frac{8}{3}$
Dann folgt:
$y = \frac{8}{3} \cdot x + b$
$x = 6$ ist Nullstelle von $f \Rightarrow$ $f (6) = 0$
Mit $P (6 | 0)$ folgt dann: $0 = \frac{8}{3} \cdot 6 + b \Rightarrow b = - 16$
Die Gleichung der Tangente t an $G_{f}$ im Punkt $P (6 | f (6))$ lautet:
$t : y = \frac{8}{3} \cdot x - 16$
Die allgemeine Tangentengleichung lautet $t : y = m \cdot x + b$ .
Weiterhin ist $m = f^{'} (6)$ und $x = 6$ ist Nullstelle von $f \Rightarrow$ $f (6) = 0$ , also hat $P$ die Koordinaten $(6 | 0)$ .

(i) Die Tangente $t$ hat mit $G_{f}$ neben $P$ nur den Punkt $Q (- 12 | f (- 12))$ gemeinsam. Geben Sie die Gleichung einer Stammfunktion der Funktion $d$ mit $d (x) = f (x) - (\frac{8}{3} x - 16)$ an und berechnen Sie den Inhalt der Fläche, die $G_{f}$ und t einschließen. (4 P)
(ii) Die von $G_{f}$ und $t$ eingeschlossene Fläche wird durch die $y$ -Achse in zwei Teilflächen unterteilt.
Ermitteln Sie den Anteil der linken Teilfläche an der von $G_{f}$ und $t$ eingeschlossenen Gesamtfläche. (3 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
(i) Gib die Gleichung einer Stammfunktion der Funktion $d$ mit $d (x) = f (x) - (\frac{8}{3} x - 16)$ an
Es ist $d (x) = f (x) - (\frac{8}{3} x - 16) = \frac{1}{27} x^{3} - \frac{4}{3} x - (\frac{8}{3} x - 16) = \frac{1}{27} x^{3} - 4 x + 16$ .
Damit erhält man eine Stammfunktion $D$ von $d$ :
$D (x) = \frac{1}{108} x^{4} - 2 x^{2} + 16 x$ .
Berechne den Inhalt der Fläche, die $G_{f}$ und t einschließen
Bekannt ist: Die Tangente $t$ hat mit $G_{f}$ neben $P$ nur den Punkt $Q (- 12 | f (- 12))$ gemeinsam und die Tangente $t$ an $G_{f}$ geht durch den Punkt $P (6 | f (6)) = P (6 | 0)$ .
Damit ergeben sich die Grenzen für die Berechnung des Flächeninhalts, den $G_{f}$ und $t$ einschließen.
Berechne das Integral $A_{gesamt} = \int_{- 12}^{6} d (x) d x = {[D (x)]}_{- 12}^{6} = D (6) - D (- 12) = 324$ .
Der Inhalt der Fläche, die $G_{f}$ und $t$ einschließen, beträgt $324 FE$ .
(ii) Ermittele den Anteil der linken Teilfläche an der von $G_{f}$ und $t$ eingeschlossenen Gesamtfläche
Bekannt ist, dass die von $G_{f}$ und $t$ eingeschlossene Fläche durch die $y$ -Achse in zwei Teilflächen unterteilt wird.
Die linke Teilfläche verläuft von $x = - 12$ bis $x = 0$ .
$\Rightarrow A_{links} = \int_{- 12}^{0} d (x) d x = 288$
Der Inhalt der linken Teilfläche, die $G_{f}$ und $t$ einschließen, beträgt $288 FE$ .
Gesucht ist nun das Verhältnis der beiden Flächen:
$\frac{A_{links}}{A_{gesamt}} = \frac{\int_{- 12}^{0} d (x) d x}{\int_{- 12}^{6} d (x) d x} = \frac{288}{324} = \frac{8}{9}$
$\frac{8}{9} \approx 0,889 = 88,9 %$
Der Anteil der linken Teilfläche an der von $G_{f}$ und $t$ eingeschlossenen Gesamtfläche beträgt rund $88,9 %$ .
(i)
Es ist $d (x) = f (x) - (\frac{8}{3} x - 16) = \frac{1}{27} x^{3} - 4 x + 16$ .
Bestimme die Stammfunktion $D (x)$ von $d (x)$ .
Es sind $Q (- 12 | f (- 12))$ und $P (6 | f (6)) = P (6 | 0)$ bekannt $\Rightarrow$ Grenzen für die Flächenberechnung.
Berechne mit $D (x)$ das Integral $A_{gesamt} = \int_{- 12}^{6} d (x) d x$ .
(ii)
Die linke Teilfläche verläuft von $x = - 12$ bis $x = 0$ . Berechne $A_{links}$ .
Gesucht ist das Verhältnis der beiden Flächen $\frac{A_{links}}{A_{gesamt}}$ .
2
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 2
Die Aufgabe 2 ist eine Fortsetzung der Aufgabe 1.
Gegeben ist die in $ℝ$ definierte Funktion $f$ mit $f (x) = \frac{1}{27} x^{3} - \frac{4}{3} x$ . Ihr Graph ist $G_{f}$ .
Aus $G_{f}$ werden in drei Schritten neue Graphen erzeugt. Die drei Schritte sind:
Spiegeln an der $x$ -Achse.
Verschieben um $6$ in positive $x$ -Richtung.
Verschieben um $14$ in positive $y$ -Richtung.
Jeder Schritt wird genau einmal ausgeführt, nur die Reihenfolge kann verändert werden. Es wird jeweils nur der neue Graph nach Ausführung aller drei Schritte betrachtet.
Geben Sie an, wie viele verschiedene neue Graphen aus $G_{f}$ auf diese Art erzeugt werden können.
Begründen Sie Ihre Angabe. (4 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Transformationen von Funktionen
Begründe Deine Angabe
Das Ergebnis der Veränderung ist unabhängig von der Position der Verschiebung in $x$ -Richtung. Wesentlich ist nur die Reihenfolge der beiden anderen Schritte. Abhängig davon geht beispielsweise der Wendepunkt $(0 | 0)$ durch die drei Schritte entweder in $(6 | 14)$ oder $(6 | - 14)$ über.
Folglich entstehen zwei verschiedene neue Graphen.
Die folgende Angabe ist nicht in der Aufgabenstellung gefordert. Die dient nur zur Erklärung. Die zwei möglichen neuen Funktionen sind:
$f (x)^{*} = - \frac{1}{27} (x - 6)^{3} + \frac{4}{3} (x - 6) + 14$ und
$f (x)^{* *} = - \frac{1}{27} (x - 6)^{3} + \frac{4}{3} (x - 6) - 14$
Das Ergebnis der Veränderung ist unabhängig von der Position der Verschiebung in $x$ -Richtung.
Wesentlich ist nur die Reihenfolge der beiden anderen Schritte.
3
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 3
Gegeben ist die in $ℝ$ definierte Funktion $f$ mit $f (x) = \frac{1}{27} x^{3} - \frac{4}{3} x$ . Ihr Graph ist $G_{f}$ .
Aus $G_{f}$ werden in drei Schritten neue Graphen erzeugt. Die drei Schritte sind:
Spiegeln an der x-Achse.
Verschieben um 6 in positive x-Richtung.
Verschieben um 14 in positive y-Richtung.
Wird $G_{f}$ den drei Schritten in der angegebenen Reihenfolge unterzogen, so entsteht der Graph der in der Aufgabe 3 betrachteten Funktion $g$ .
Abbildung 1 zeigt den Graphen der in $ℝ$ definierten Funktion $g$ mit $g (x) = - \frac{1}{27} x \cdot (x - 6) \cdot (x - 12) + 14$ .
In einem Modell, das aus langjährigen Messungen gewonnen wurde, beschreibt $g$ für $0 \leq x < 12$ den Verlauf der Tagesdurchschnittstemperatur an einem bestimmten Ort. Dabei ist $x$ die seit einem bestimmten Tag des Kalenderjahres vergangene Zeit in Monaten und $g (x)$ die Temperatur in $^{\circ} C$ .
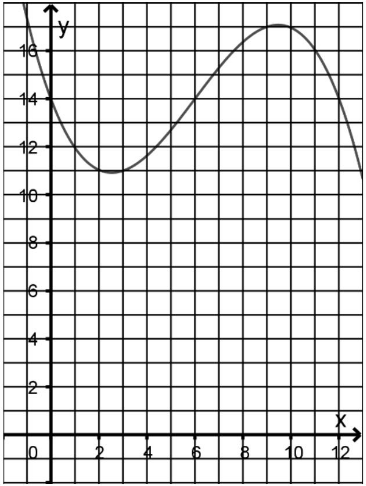
Abbildung 1
Ermitteln Sie, wie lange die Tagesdurchschnittstemperatur an dem Ort innerhalb eines Jahres über $15^{\circ} C$ liegt. (2 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionswert
Ermittele, wie lange die Tagesdurchschnittstemperatur an dem Ort innerhalb eines Jahres über $15^{\circ} C$ liegt
Löse die Gleichung $g (x) = 15$ .
Die Gleichung hat drei Lösungen $x_{1}, x_{2}$ und $x_{3}$ mit $x_{1} \approx - 0,345$ , $x_{2} \approx 6,762$ und $x_{3} \approx 11,582$ . $x_{1}$ liegt außerhalb des Modellierungsbereichs.
Unter Verwendung von Abbildung 1 gilt damit:
Zwischen $x_{2}$ und $x_{3}$ und damit über einen Zeitraum von etwa fünf Monaten liegt die Tagesdurchschnittstemperatur über $15^{\circ} C$ .
Löse die Gleichung $g (x) = 15$ .

Geben Sie die Wendestelle von $g$ an.
Beschreiben Sie die Bedeutung dieser Wendestelle hinsichtlich des Verlaufs der Tagesdurchschnittstemperatur. (1 P + 1 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wendepunkte und Terrassenpunkte
Gib die Wendestelle von $g$ an
Betrachte den Graphen von $g$ .
Wegen der Punktsymmetrie des Graphens zum Wendepunkt $(6 | 14)$ liegt die Wendestelle bei $x = 6$ .
Beschreibe die Bedeutung dieser Wendestelle hinsichtlich des Verlaufs der Tagesdurchschnittstemperatur
Die Wendestelle gibt an, wann die Tagesdurchschnittstemperatur im Modell am stärksten zunimmt.
Betrachte den Graphen von $g$ und lies den Wendepunkt ab.

Die folgenden Rechnungen stellen in Verbindung mit Abbildung 1 die Lösung einer Aufgabe im Sachzusammenhang dar:
$\begin{aligned} g^{'} (x) = 0 \Leftrightarrow x = 6 - \sqrt{12} \lor x = 6 + \sqrt{12} . \\ g (6 + \sqrt{12}) - g (6 - \sqrt{12}) \approx 6,2. \end{aligned}$
Geben Sie eine passende Aufgabenstellung an und erläutern Sie den dargestellten Lösungsweg. (2 P + 2 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
Gib eine passende Aufgabenstellung an und erläutere den dargestellten Lösungsweg
Eine mögliche Aufgabenstellung könnte lauten:
Ermitteln Sie die Differenz zwischen der höchsten und der niedrigsten Tagesdurchschnittstemperatur.
Erläuterung: In der ersten Zeile werden die möglichen Extremstellen von $g$ bestimmt. Anhand von Abbildung 1 wird ersichtlich, dass diese Stellen tatsächlich absolute Extremstellen im Modellierungsbereich sind. In der zweiten Zeile wird die Differenz zwischen den zugehörigen Funktionswerten berechnet.
Was wird in der ersten Zeile berechnet?
Was stellt dann die Differenz $g (x_{2}) - g (x_{1})$ dar?

Für einen anderen Ort ist der Verlauf der Tagesdurchschnittstemperatur ab einem bestimmten Tag des Kalenderjahres in Abbildung 2 modellhaft dargestellt.
Abbildung 2
(i) Begründen Sie, dass eine ganzrationale Funktion zur Modellierung des in Abbildung 2 dargestellten Verlaufs mindestens den Grad $4$ haben sollte.
Der Verlauf soll mithilfe einer ganzrationalen Funktion $h$ mit
$h (x) = a \cdot x^{4} + b \cdot x^{3} + c \cdot x^{2} + d \cdot x + e, x \in ℝ, a, b, c, d, e \in ℝ$ , modelliert werden. Dabei soll $x$ die seit dem bestimmten Tag des Kalenderjahres vergangene Zeit in Monaten und $h (x)$ die Tagesdurchschnittstemperatur in $^{\circ} C$ sein. (2 P)
(ii) Bei der Modellierung mit der Funktion $h$ sollen folgende Bedingungen erfüllt sein:
Die geringste Tagesdurchschnittstemperatur liegt bei $x = 1$ vor, die höchste Tagesdurchschnittstemperatur von $17^{\circ} C$ liegt bei $x = 7$ vor. Bei $x = 10,5$ nimmt die Tagesdurchschnittstemperatur mit einer Rate von $- {4,2}^{\circ} C$ pro Monat am schnellsten ab.
Stellen Sie aus diesen Bedingungen ein Gleichungssystem zur Berechnung von $a, b, c, d$ und $e$ auf.
[Eine Berechnung der Werte muss nicht durchgeführt werden.] (3 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Steckbriefaufgaben
(i) Begründe, dass eine ganzrationale Funktion zur Modellierung des in Abbildung 2 dargestellten Verlaufs mindestens den Grad $4$ haben sollte
In Abbildung 2 sind zwei Wendestellen zu erkennen, was bei einer ganzrationalen Funktion mindestens den Grad $4$ erfordert.
(ii) Stelle aus diesen Bedingungen ein Gleichungssystem zur Berechnung von $a, b, c, d$ und $e$ auf
Ansatz: $h (x) = a \cdot x^{4} + b \cdot x^{3} + c \cdot x^{2} + d \cdot x + e$
Für die $5$ unbekannten Parameter werden $5$ Gleichungen benötigt.
Gegeben:
1. Die geringste Tagesdurchschnittstemperatur liegt bei $x = 1$ vor $\Rightarrow$ Tiefpunkt bei $x = 1 \Rightarrow h^{'} (1) = 0$ .
2. Die höchste Tagesdurchschnittstemperatur von $17^{\circ} C$ liegt bei $x = 7$ vor.
$\Rightarrow$ $h (7) = 17$ und $h^{'} (7) = 0$ .
3. Bei $x = 10,5$ nimmt die Tagesdurchschnittstemperatur mit einer Rate von $- {4,2}^{\circ} C$ pro Monat am schnellsten ab. $\Rightarrow h^{'} (10,5) = - 4,2$ und $h^{''} (10,5) = 0$ .
Damit ergibt sich folgendes Gleichungssystem:
$| \begin{array}{l} h^{'} (1) = 0 \\ h (7) = 17 \\ h^{'} (7) = 0 \\ h^{'} (10,5) = - 4,2 \\ h^{''} (10,5) = 0 \end{array} |$
(i)
Wie viele Wendestellen sind in Abbildung 2 zu erkennen. Was folgt daraus?
(ii)
Für die $5$ unbekannten Parameter werden $5$ Gleichungen benötigt.
1. Die geringste Tagesdurchschnittstemperatur liegt bei $x = 1$ vor. Was bedeutet das für $h^{'} (1)$ ?
2. Die höchste Tagesdurchschnittstemperatur von $17^{\circ} C$ liegt bei $x = 7$ vor. $\Rightarrow$ dazu gehört der Punkt $(7 | 17)$ und was bedeutet das für $h^{'} (7)$ ?
3. Bei $x = 10,5$ nimmt die Tagesdurchschnittstemperatur mit einer Rate von $- {4,2}^{\circ} C$ pro Monat am schnellsten ab. Was bedeutet das für $h^{'} (10,5)$ ? Bei $x = 10,5$ gibt es einen Wendepunkt. Was bedeutet das für $h^{''} (10,5)$ ?

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org

B2

Aufgabe 1

Begründe, dass Gf symmetrisch bezüglich seines Wendepunktes ist

Bestimme die Koordinaten der Schnittpunkte von Gf mit den Koordinatenachsen

Erkläre das Ergebnis

Zeige, dass einer der beiden ein Tiefpunkt mit der x-Koordinate 12 ist

Bestimme eine Gleichung der Tangente t an Gf im Punkt P(6|f(6))

(i) Gib die Gleichung einer Stammfunktion der Funktion d mit d(x)=f(x)−(83x−16) an

Berechne den Inhalt der Fläche, die Gf und t einschließen

(ii) Ermittele den Anteil der linken Teilfläche an der von Gf und t eingeschlossenen Gesamtfläche

Aufgabe 2

Begründe Deine Angabe

Aufgabe 3

Ermittele, wie lange die Tagesdurchschnittstemperatur an dem Ort innerhalb eines Jahres über 15∘C liegt

Gib die Wendestelle von g an

Beschreibe die Bedeutung dieser Wendestelle hinsichtlich des Verlaufs der Tagesdurchschnittstemperatur

Gib eine passende Aufgabenstellung an und erläutere den dargestellten Lösungsweg

(i) Begründe, dass eine ganzrationale Funktion zur Modellierung des in Abbildung 2 dargestellten Verlaufs mindestens den Grad 4 haben sollte

(ii) Stelle aus diesen Bedingungen ein Gleichungssystem zur Berechnung von a,b,c,d und e auf

Begründe, dass $G_{f}$ symmetrisch bezüglich seines Wendepunktes ist

Bestimme die Koordinaten der Schnittpunkte von $G_{f}$ mit den Koordinatenachsen

Zeige, dass einer der beiden ein Tiefpunkt mit der $x$ -Koordinate $\sqrt{12}$ ist

Bestimme eine Gleichung der Tangente t an $G_{f}$ im Punkt $P (6 | f (6))$

(i) Gib die Gleichung einer Stammfunktion der Funktion $d$ mit $d (x) = f (x) - (\frac{8}{3} x - 16)$ an

Berechne den Inhalt der Fläche, die $G_{f}$ und t einschließen

(ii) Ermittele den Anteil der linken Teilfläche an der von $G_{f}$ und $t$ eingeschlossenen Gesamtfläche

Ermittele, wie lange die Tagesdurchschnittstemperatur an dem Ort innerhalb eines Jahres über $15^{\circ} C$ liegt

Gib die Wendestelle von $g$ an

(i) Begründe, dass eine ganzrationale Funktion zur Modellierung des in Abbildung 2 dargestellten Verlaufs mindestens den Grad $4$ haben sollte

(ii) Stelle aus diesen Bedingungen ein Gleichungssystem zur Berechnung von $a, b, c, d$ und $e$ auf