Teil 2, Analysis II

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe-Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Das Landesamt für Umwelt ist unter anderem dafür zuständig, vor Überflutungen durch Flüsse zu warnen und lässt dazu täglich kontinuierlich die Wasserstände diverser Flüsse überprüfen. Der Wasserstand eines bestimmten Flusses im März des Jahres 2010 kann vereinfacht durch die Funktion $w$ mit der Funktionsgleichun $w (t) = a t^{4} + b t^{3} + c$ mit geeigneten Werten $a, b, c \in ℝ$ und der Definitionsmenge $D_{w} = [0; 30]$ beschrieben werden. Dabei bedeutet die Variable $t$ die Zeit in Tagen ab Monatsbeginn zum Zeitpunkt $t_{0} = 0$ . Der Funktionswert $w (t)$ gibt den Wasserstand des Flusses in $cm$ an. Zu Monatsbeginn lag der Wasserstand bei $200 cm$ und am Monatsende bei $308 cm$ . Der höchste Wasserstand wurde am 25. März – also zum Zeitpunkt $t_{m a x} = 24$ – gemessen. Der abgebildete Graph zeigt den Wasserstand $w (t)$ in Abhängigkeit von der Zeit $t$ .
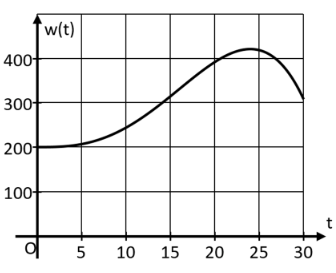
Auf das Mitführen von Einheiten während der Rechnungen kann verzichtet werden. Runden Sie Ihre Ergebnisse – falls nicht anders gefordert – sinnvoll.
Bestimmen Sie die Werte der Parameter $a, b$ und $c$ und damit die zugehörige Funktionsgleichung von $w$ .
[Mögliches Ergebnis: $w (t) = - \frac{1}{500} (t^{4} - 32 t^{3} - 100000)$ ]

Berechnen Sie den höchsten Pegel im Beobachtungszeitraum zentimetergenau.

Ermitteln Sie rechnerisch das Datum im Beobachtungszeitraum, an dem die Änderungsgeschwindigkeit des Pegelstandes am größten war.

Berechnen Sie $\frac{1}{30} \int_{0}^{30} w (t) d t$ und interpretieren Sie das Ergebnis im Sinne der vorliegenden Thematik.
2
Gegeben ist die Funktion $f : x \mapsto x^{2} \cdot e^{- x}$ mit der Definitionsmenge $D_{f} = ℝ .$
Geben Sie die Nullstelle der Funktion $f$ an und untersuchen Sie das Verhalten der Funktionswerte $f (x)$ für $x \to - \infty$ und $x \to \infty .$

Bestimmen Sie die maximalen Intervalle, in denen der Graph der Funktion $f$ streng monoton steigt bzw. streng monoton fällt, und damit die Art und Koordinaten der relativen Extrempunkte des Graphen von $f$ .

Zeichnen Sie den Graphen der Funktion $f$ unter Verwendung aller bisherigen Ergebnisse im Bereich $- 1 \leq x \leq 6$ in ein geeignetes Koordinatensystem.
Maßstab für beide Achsen: $1$ LE $1 cm$
3
Der Bestand einer Bakterienkultur, der kontinuierlich Gift zugeführt wird, kann in den ersten fünf Stunden näherungsweise durch eine Funktion des folgenden Typs beschrieben werden:
$k : t \mapsto 50 t \cdot e^{- a t} + 10$ mit $t \in [0; 5]$
Dabei gibt $t$ die seit Beginn der Giftzugabe zum Zeitpunkt $t_{0} = 0$ vergangene Zeit in Stunden an. Der Funktionswert $k (t)$ gibt die Anzahl der Bakterien in Tausend an. Je nach Wirksamkeit des Gifts ist $a$ eine dem Gift entsprechende positive reelle Zahl. Auf das Mitführen von Einheiten während der Rechnungen wird verzichtet. Runden Sie Ihre Ergebnisse sinnvoll. Die Abbildung zeigt drei Ausschnitte von Graphen der Funktion $k$ für drei verschiedene Werte für $a$ .
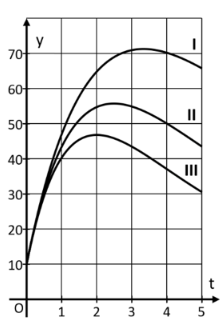
Graph I gilt für $a_{1} = 0,3$ mit $k_{I} (t) = 50 t \cdot e^{- 0,3 t} + 10$
Graph II gilt für $0,3 < a_{2} < 0,5$ mit $k_{I I} (t) = 50 t \cdot e^{- a_{2} t} + 10$
Graph III gilt für $a_{3} = 0,5$ mit $k_{I I I} (t) = 50 t \cdot e^{- 0,5 t} + 10$
Berechnen Sie für $t_{1} = 0$ und $t_{2} = 2$ den Quotienten $\frac{k_{I I I} (t_{2}) - k_{I I I} (t_{1})}{t_{2} - t_{1}}$ und interpretieren Sie das Ergebnis im Sachzusammenhang.

Überprüfen Sie bei der Funktion $k_{I I I}$ rechnerisch, ob vier Stunden nach Beginn der Giftzugabe die momentane Abnahmerate der Anzahl der Bakterien ca. $113$ Bakterien pro Minute beträgt.

Entnehmen Sie der Abbildung ein geeignetes Wertepaar von Graph II und berechnen Sie damit den Wert $a_{2}$ für den Funktionsterm $k_{I I} (t)$ . Folgern Sie aus den Angaben und dem berechneten Wert für $a_{2}$ , wie die Größe von $a$ mit der Wirksamkeit des Gifts zusammenhängt.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org