Nachtermin Teil B
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe-Prüfungen
Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
Nutze unser Training Realschule Bayern (Abschlussprüfung) und rechne dich fit für die Prüfung. Du findest dort einen Überblick über alle Themen und viele weitere Übungsmöglichkeiten.
- 1
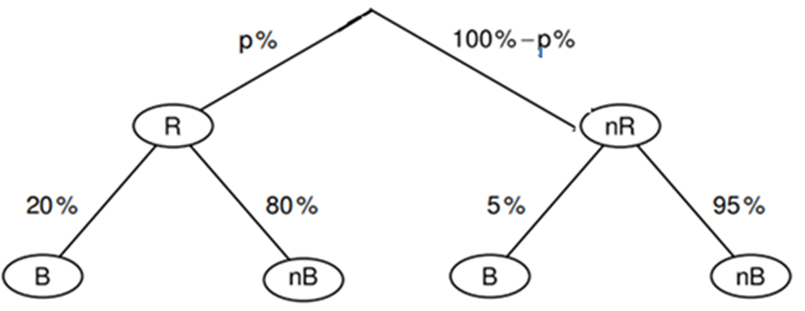
Aufgabe B1
In einem Supermarkt werden regionale („R“) und nichtregionale („nR“) Produkte angeboten. Dabei beträgt der Anteil der regionalen Produkte .
Alle Produkte sind entweder biologisch („B“) oder nichtbiologisch („nB“) erzeugt.
der regionalen Produkte des Supermarkts sind biologisch erzeugt. Bei den nichtregionalen Produkten sind dies nur .
Zeichnen Sie ein zugehöriges Baumdiagramm, in dem alle prozentualen Anteile ersichtlich sind. (2,5 P)
In diesem Supermarkt findet eine Warenkontrolle statt. Bei der zufälligen Auswahl eines Produktes erhält man mit einer Wahrscheinlichkeit von ein regionales, biologisch erzeugtes Produkt.
Berechnen Sie den Anteil aller regionalen Produkte dieses Supermarkts in Prozent. (1,5 P)
Dieser Supermarkt bietet insgesamt Produkte an.
Berechnen Sie die Anzahl der regionalen, biologisch erzeugten Produkte. (1 P)
- 2
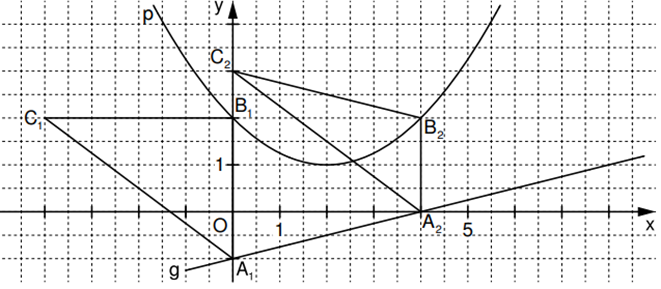
Aufgabe B2
Gegeben sind die Parabel mit der Gleichung und die
Gerade mit der Gleichung .
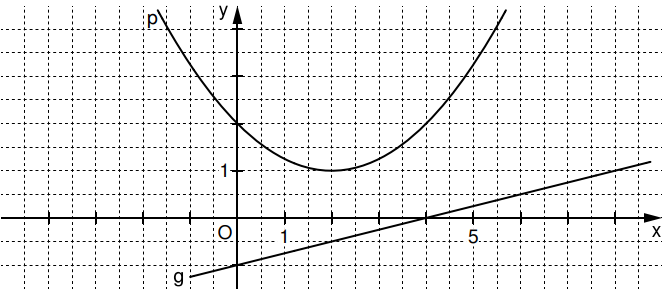
Punkte auf der Geraden und Punkte auf der
Parabel haben dieselbe Abszisse . Sie sind zusammen mit Punkten Eckpunkte von Dreiecken . Es gilt: .
Zeichnen Sie die Dreiecke für und für in das
Koordinatensystem der Aufgabenstellung ein. (2 P)
Zeigen Sie rechnerisch, dass für die Länge der Strecken in Abhängigkeit von der Abszisse der Punkte gilt: . (1 P)
Die Dreiecke und sind gleichschenklig mit der Basis bzw. . Berechnen Sie die zugehörigen Werte von . (3 P)
Runden Sie auf zwei Stellen nach dem Komma.
- 3
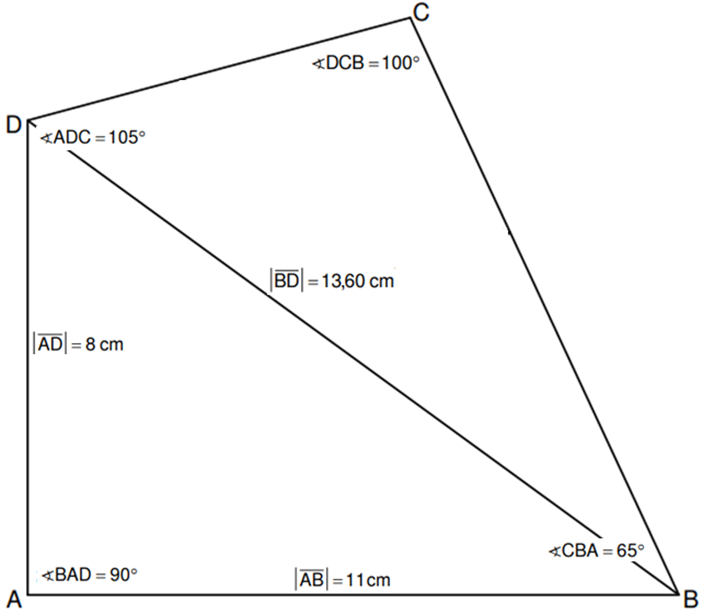
Aufgabe B3
Die nebenstehende Skizze zeigt das Viereck .
Es gilt: ; ;
; ; .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
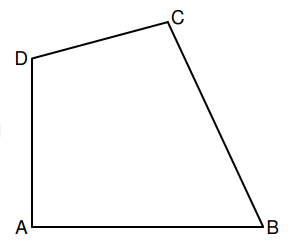
Zeichnen Sie das Viereck und die Strecke .
Berechnen Sie sodann das Maß des Winkels und die Länge der Strecke . (3,5 P)
Teilergebnisse:
Berechnen Sie die Längen der Strecken und . (4 P)
Zwischenergebnis: ; Teilergebnis
Bestimmen Sie den Flächeninhalt des Vierecks . (2 P)
Ergebnis:
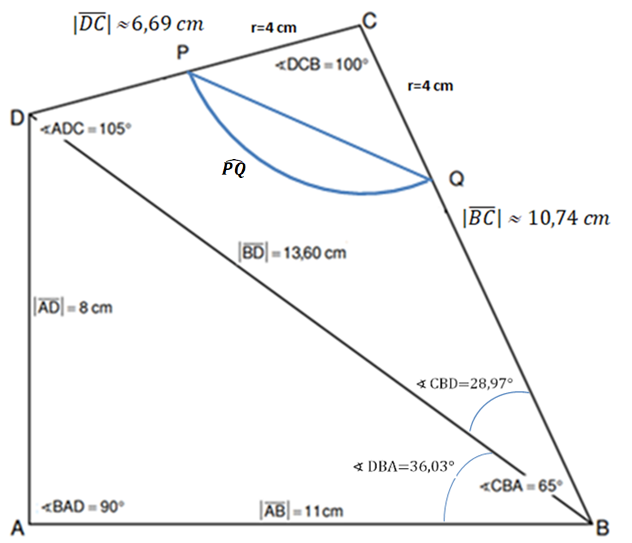
Der Kreis mit dem Mittelpunkt und dem Radius schneidet die Strecke im Punkt und die Strecke im Punkt .
Ergänzen Sie in der Zeichnung zu Aufgabe a) den Kreisbogen mit dem Mittelpunkt und die Strecke . (1 P)
Der Kreisbogen und die Strecke begrenzen eine Figur.
Berechnen Sie den Umfang dieser Figur. (2,5 P)
Berechnen Sie den prozentualen Anteil des Flächeninhalts der Figur aus e) am
Flächeninhalt des Vierecks . (3 P)
- 4
Aufgabe B4
Das Drachenviereck mit der Symmetrieachse und dem Diagonalenschnittpunkt ist die
Grundfläche der Pyramide mit der Höhe .
Es gilt: ; ;
; .
Die nebenstehende Skizze zeigt ein Schrägbild der Pyramide .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
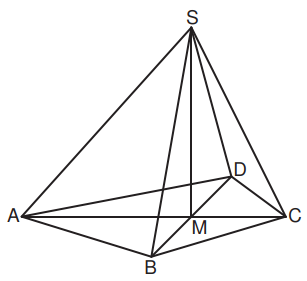
Zeichnen Sie das Schrägbild der Pyramide , wobei auf der Schrägbildachse und der Punkt links vom Punkt liegen soll.
Für die Zeichnung gilt: ;
Berechnen Sie sodann die Länge der Strecke und das Maß des Winkels . (4 P)
Teilergebnisse:
Für Punkte und gilt: und mit und . Die Punkte sind die Spitzen von Pyramiden mit den Grundflächen und den Höhen .
Zeichnen Sie die Pyramide und die Höhe für in das Schrägbild zu a) ein.
Berechnen Sie sodann die Länge der Strecke . (4 P)
Bestimmen Sie durch Rechnung, um wie viel Prozent das Volumen der
Pyramide kleiner ist als das Volumen der Pyramide . (4 P)
Zwischenergebnis:
Für die Pyramide gilt: .
Berechnen Sie den zugehörigen Wert für . (2 P)
In der Pyramide hat der Winkel das Maß .
Bestimmen Sie den zugehörigen Wert für . (2 P)