Nachtermin Teil A
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe-Prüfungen
Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Aufgabe A1
Die Skizze zeigt den Axialschnitt eines Rotationskörpers mit der Rotationsachse . Der Punkt ist der Schnittpunkt der Geraden und .
Es gilt: ; ; ;
; ;
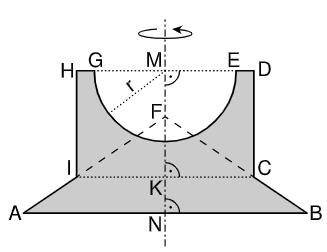
Berechnen Sie das Volumen des Rotationskörpers.
Runden Sie auf zwei Stellen nach dem Komma. (5 P)
Zwischenergebnis:
- 2
Aufgabe A2
Gegeben ist das Dreieck mit den Seitenlängen , und .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
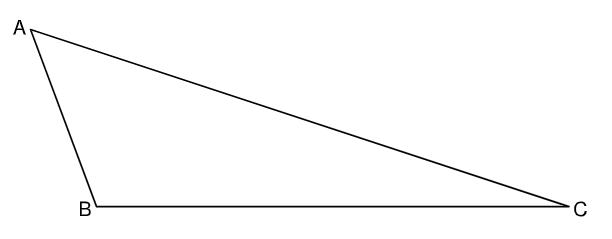
Berechnen Sie das Maß des Winkels . (2 P)
Ergebnis:
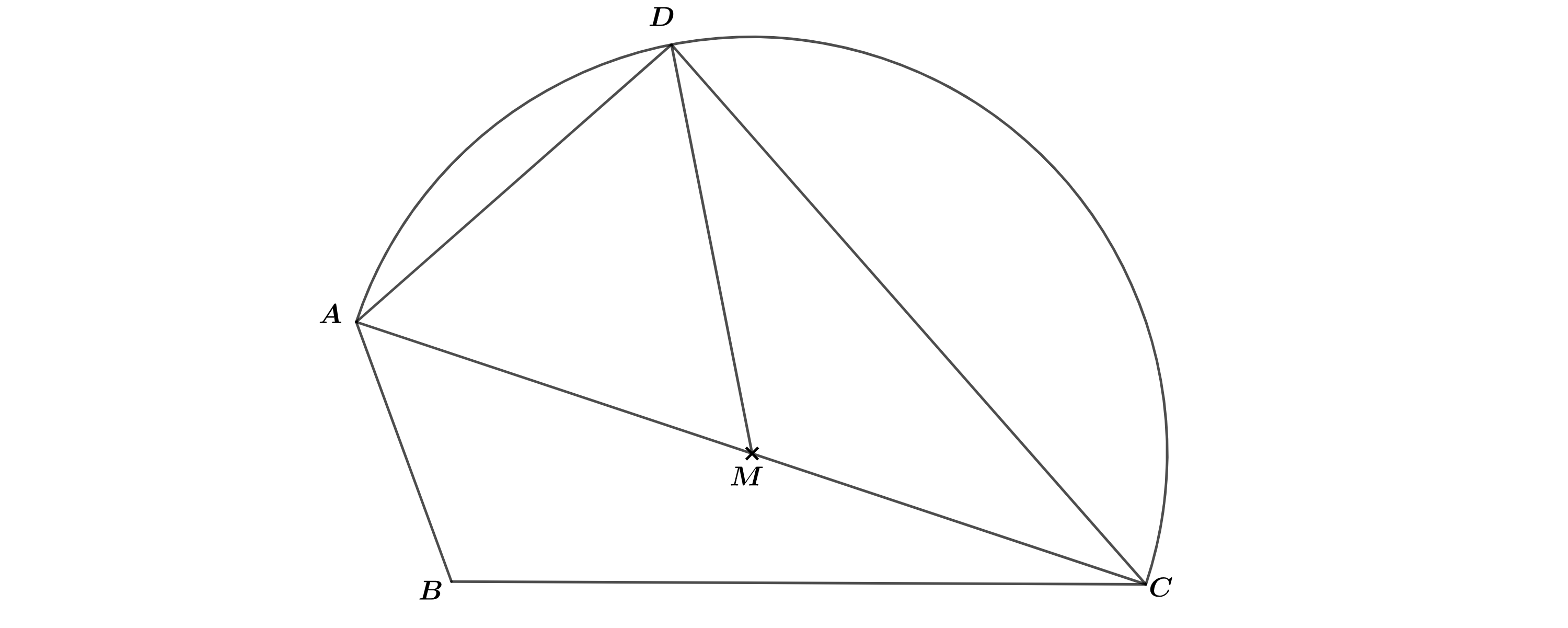
Der Punkt ist der Mittelpunkt der Strecke . Auf dem Kreisbogen mit dem Mittelpunkt liegt der Punkt mit .
Zeichnen Sie den Kreisbogen , das Dreieck und die Strecke in die Zeichnung zu 2) ein. (2 P)
Begründen Sie, weshalb der Winkel das Maß und der Winkel das Maß hat. (2 P)
Berechnen Sie den Flächeninhalt der Figur, die durch den Kreisbogen sowie die Strecken , und begrenzt wird. (3 P)
- 3
Aufgabe A3
An zwei Türmen sind auf einer Höhe von jeweils über dem Boden Plattformen angebracht. Zwischen den beiden voneinander entfernten Plattformen ist eine Brücke gespannt. Der Verlauf der Brücke zwischen den Punkten und kann näherungsweise durch eine Parabel beschrieben werden. Diese hat eine Gleichung der Form
, ;
und den Scheitelpunkt . Dabei entspricht der horizontal gemessenen Entfernung vom Punkt und der Höhe über dem Boden.
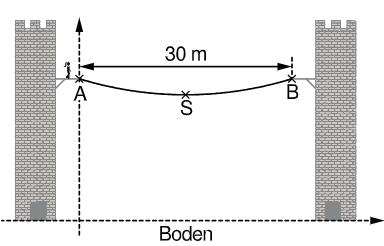
Zeigen Sie rechnerisch, dass für die Gleichung der Parabel gilt:
, . (3 P)
Eine Person überquert die Brücke von nach . Sie geht bereits wieder aufwärts. Bei einer Höhe von Metern über dem Boden bleibt sie stehen. Diese Position entspricht dem Punkt auf der Parabel .
Berechnen Sie die x-Koordinate des Punktes (2 P)