Beispiele für lineare Abbildungen

Streckung in $x$ -Richtung

Unser erstes Beispiel ist die Streckung um den Faktor $β$ in $x$ -Richtung in der Ebene $ℝ^{2}$ . Dabei wird jeder Vektor $a = (a_{x}, a_{y})^{T} \in ℝ^{2}$ abgebildet auf $f (a) = (β a_{x}, a_{y})^{T}$ . Die folgende Grafik zeigt diese Abbildung für $β = 2$ . Die $y$ -Koordinate bleibt dabei gleich und die $x$ -Koordinate wird verdoppelt:

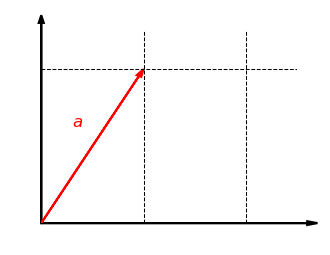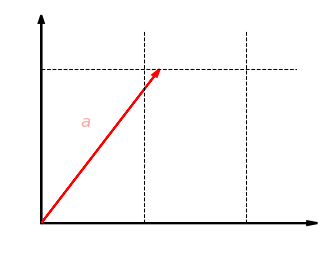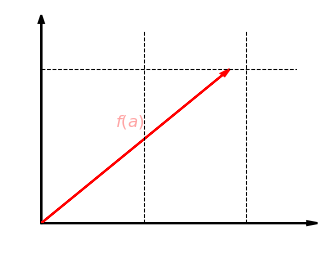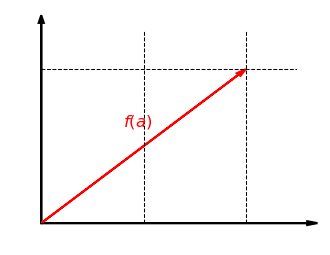
Schauen wir uns nun an, ob diese Abbildung verträglich mit der Addition ist. Nehmen wir also zwei Vektoren $a$ und $b$ , bilden die Summe $a + b$ und strecken diese dann in $x$ -Richtung. Das Ergebnis ist dasselbe, als wenn wir beide Vektoren zuerst in $x$ -Richtung strecken und dann addieren:

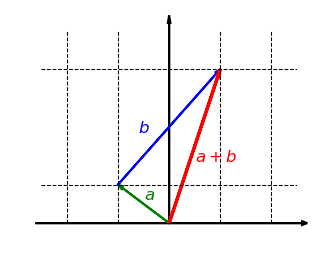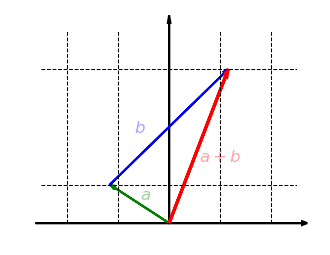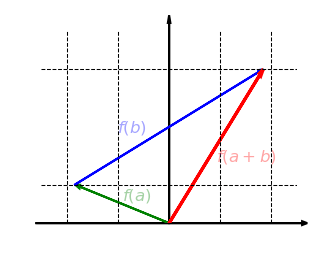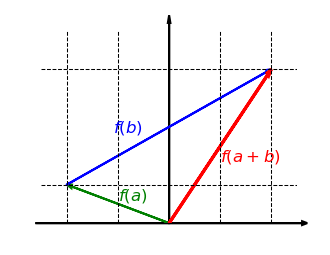
as lässt sich auch mathematisch zeigen. Unsere Abbildung ist die Funktion $f : ℝ^{2} \to ℝ^{2}, f ((x, y)^{T}) = (β x, y)^{T}$ . Wir können nun die Eigenschaft $f (a + b) = f (a) + f (b)$ nachprüfen:

\begin{array}{ll} f (a + b) & = f ((\begin{array}{c} a_{x} \\ a_{y} \end{array}) + (\begin{array}{c} b_{x} \\ b_{y} \end{array})) \\ = f ((\begin{array}{c} a_{x} + b_{x} \\ a_{y} + b_{y} \end{array})) \\ = (\begin{array}{c} β (a_{x} + b_{x}) \\ a_{y} + b_{y} \end{array}) \\ = (\begin{array}{c} β a_{x} + β b_{x} \\ a_{y} + b_{y} \end{array}) \\ = (\begin{array}{c} β a_{x} \\ a_{y} \end{array}) + (\begin{array}{c} β b_{x} \\ b_{y} \end{array}) \\ = f ((\begin{array}{c} a_{x} \\ a_{y} \end{array})) + f ((\begin{array}{c} b_{x} \\ b_{y} \end{array})) \\ = f (a) + f (b) \end{array}

Schauen wir uns nun die Verträglichkeit mit der skalaren Multiplikation an. Die folgende Grafik zeigt, dass es egal ist, ob der Vektor $a$ zuerst mit einem Faktor $λ$ skaliert und dann in $x$ -Richtung gestreckt wird oder zuerst in $x$ -Richtung gestreckt und dann mit $λ$ skaliert wird:

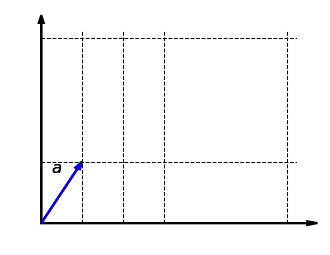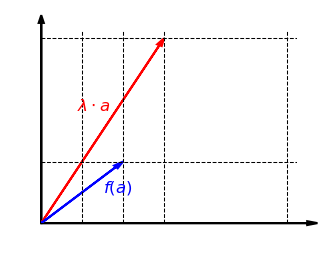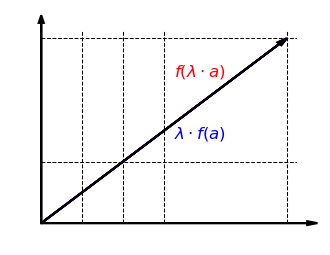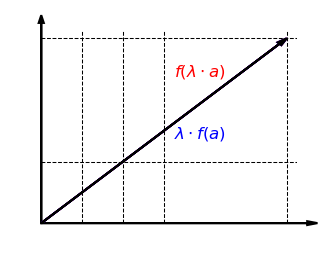
Auch das lässt sich formal zeigen: Für $a \in ℝ^{2}$ und $λ \in ℝ$ gilt

\begin{array}{cl} f (λ a) & = f (λ (\begin{array}{c} a_{x} \\ a_{y} \end{array})) = f ((\begin{array}{c} λ a_{x} \\ λ a_{y} \end{array})) \\ = (\begin{array}{c} β (λ a_{x}) \\ λ a_{y} \end{array}) = (\begin{array}{c} λ β a_{x} \\ λ a_{y} \end{array}) \\ = λ (\begin{array}{c} β a_{x} \\ a_{y} \end{array}) = λ f ((\begin{array}{c} a_{x} \\ a_{y} \end{array})) \\ = λ f (a) . \end{array}

Damit ist unser f eine lineare Abbildung.

Drehungen

Im Folgenden betrachten wir eine Drehung $D_{α}$ der Ebene um den Winkel $α$ (gegen den Uhrzeigersinn gemessen) mit dem Ursprung als Drehzentrum. Es handelt sich dabei also um eine Abbildung $D_{α} : ℝ^{2} \to ℝ^{2}$ , die jedem Vektor $v \in ℝ^{2}$ den um den Winkel $α$ gedrehten Vektor $D_{α} (v) \in ℝ^{2}$ zuordnet:

Wir wollen uns jetzt davon überzeugen, dass $D_{α}$ eine lineare Abbildung ist. Dazu müssen wir zeigen:

$D_{α}$ ist additiv: Für alle $v, w \in ℝ^{2}$ ist $D_{α} (v + w) = D_{α} (v) + D_{α} (w)$ .
$D_{α}$ ist homogen: Für alle $v \in ℝ^{2}$ und $λ \in ℝ$ ist $D_{α} (λ \cdot v) = λ \cdot D_{α} (v)$ .

Überprüfen wir zunächst die Additivität, also die Gleichung $D_{α} (v + w) = D_{α} (v) + D_{α} (w)$ . Addieren wir zwei Vektoren $v, w \in ℝ^{2}$ zuerst und drehen ihre Summe v+w anschließend um den Winkel $α$ , so soll derselbe Vektor herauskommen, wie wenn wir erst die Vektoren um den Winkel $α$ drehen und im Anschluss die gedrehten Vektoren $D_{α} (v)$ und $D_{α} (w)$ addieren. Dies machen wir uns an folgenden beiden Videos klar:

Kommen wir nun zur Homogenität: $D_{α} (λ \cdot v) = λ \cdot D_{α} (v)$ . Strecken wir zunächst einen Vektor $v \in ℝ^{2}$ um einen Faktor $λ \in ℝ$ und drehen das Resultat $λ \cdot v$ danach um den Winkel $α$ , so soll derselbe Vektor herauskommen, wie wenn wir als Erstes die Drehung um den Winkel $α$ durchführen und daraufhin das Ergebnis $D_{α} (v)$ um den Faktor $λ$ skalieren. Auch dies wird durch zwei Videos ersichtlich:

Somit handelt es sich bei Drehungen im $ℝ^{2}$ um lineare Abbildungen.

Lineare Abbildung zwischen Vektorräumen unterschiedlicher Dimension

Ein Beispiel einer linearen Abbildung zwischen zwei Vektorräumen mit unterschiedlicher Dimension ist die folgende Projektion des Raums $ℝ^{3}$ auf die Ebene $ℝ^{2}$ :

f : ℝ^{3} \to ℝ^{2}; (\begin{array}{c} x \\ y \\ z \end{array}) \mapsto (\begin{array}{c} x \\ y \end{array})

Wir prüfen nun, ob die Vektoraddition erhalten bleibt. Also ob für Vektoren $a, b \in ℝ^{3}$ gilt

gilt

f (a + b) = f (a) + f (b)

Dies können wir direkt nachweisen:

\begin{array}{ll} f (a + b) & = f ((\begin{array}{c} a_{x} \\ a_{y} \\ a_{z} \end{array}) + (\begin{array}{c} b_{x} \\ b_{y} \\ b_{z} \end{array})) = f ((\begin{array}{c} a_{x} + b_{x} \\ a_{y} + b_{y} \\ a_{z} + b_{z} \end{array})) \\ = (\begin{array}{c} a_{x} + b_{x} \\ a_{y} + b_{y} \end{array}) = (\begin{array}{c} a_{x} \\ a_{y} \end{array}) + (\begin{array}{c} b_{x} \\ b_{y} \end{array}) \\ = f ((\begin{array}{c} a_{x} \\ a_{y} \\ a_{z} \end{array})) + f ((\begin{array}{c} b_{x} \\ b_{y} \\ b_{z} \end{array})) = f (a) + f (b) . \end{array}

Nun überprüfen wir die Homogenität. Für alle $λ \in ℝ$ und $a \in ℝ^{2}$ soll gelten:

f (λ \cdot a) = λ \cdot f (a) .

Es ist

\begin{array}{ll} f (λ \cdot a) & = f (λ \cdot (\begin{array}{c} a_{x} \\ a_{y} \\ a_{z} \end{array})) = f ((\begin{array}{c} λ a_{x} \\ λ a_{y} \\ λ a_{z} \end{array})) \\ = (\begin{array}{c} λ a_{x} \\ λ a_{y} \end{array}) = λ \cdot (\begin{array}{c} a_{x} \\ a_{y} \end{array}) = λ \cdot f ((\begin{array}{c} a_{x} \\ a_{y} \\ a_{z} \end{array})) \\ = λ \cdot f (a) . \end{array}

Damit ist die Projektion $f$ eine lineare Abbildung.

Eine nichtlineare Abbildung

Als nächstes untersuchen wir, ob es auch nicht lineare Abbildungen gibt. Hierzu betrachten wir die Normabbildung auf der Ebene, die jedem Vektor seine Länge zuordnet:

‖ \cdot ‖_{2} : ℝ^{2} \to ℝ; (\begin{array}{c} x \\ y \end{array}) \mapsto \sqrt{x^{2} + y^{2}}

Diese Abbildung ist keine lineare Abbildung, denn sie erhält weder die Vektoraddition noch die Skalarmultiplikation.Dies zeigen wir mit Hilfe eines Gegenbeispiels:

Wir betrachten die Vektoren $(1,0)^{T}$ und $(0,1)^{T} \in ℝ^{2}$ . Wenn wir die beiden Vektoren zuerst addieren und danach abbilden, so erhalten wir

{‖ (\begin{array}{c} 1 \\ 0 \end{array}) + (\begin{array}{c} 0 \\ 1 \end{array}) ‖}_{2} = {‖ (\begin{array}{c} 1 \\ 1 \end{array}) ‖}_{2} = \sqrt{1^{2} + 1^{2}} = \sqrt{2} .

Nun bilden wir die Vektoren zuerst ab und addieren dann die Ergebnisse:

{‖ (\begin{array}{c} 1 \\ 0 \end{array}) ‖}_{2} + {‖ (\begin{array}{c} 0 \\ 1 \end{array}) ‖}_{2} = \sqrt{1^{2} + 0^{2}} + \sqrt{0^{2} + 1^{2}} = \sqrt{1} + \sqrt{1} = 2

Also gilt

{‖ (\begin{array}{c} 1 \\ 0 \end{array}) + (\begin{array}{c} 0 \\ 1 \end{array}) ‖}_{2} \neq {‖ (\begin{array}{c} 1 \\ 0 \end{array}) ‖}_{2} + {‖ (\begin{array}{c} 0 \\ 1 \end{array}) ‖}_{2}

Damit ist gezeigt, dass die Normabbildung nicht additiv ist. Dies reicht schon aus um zu zeigen, dass die Normalabbildung nicht linear ist.

Alternativ hätten wir auch zeigen können, dass die Normalabbildung nicht homogen ist. Es gilt nämlich

{‖ (- 1) \cdot (\begin{array}{c} 1 \\ 0 \end{array}) ‖}_{2} = {‖ (\begin{array}{c} - 1 \\ 0 \end{array}) ‖}_{2} = \sqrt{(- 1)^{2} + 0^{2}} = 1 \neq - 1 = (- 1) \cdot {‖ (\begin{array}{c} 1 \\ 0 \end{array}) ‖}_{2} .

Angewandte Beispiele

Lineare Abbildungen werden in vielen Bereichen verwendet, ohne dass wir uns dessen bewusst sind:

Lineare Abbildungen sind eine der einfachsten Formen einer Abbildung. So werden komplexere Abbildungen häufig durch lineare Abbildungen approximiert.
Der bekannteste Fall, in dem uns lineare Abbildungen das Leben erleichtern, sind Computergrafiken. Jedes Skalieren eines Fotos oder einer Grafik ist eine lineare Abbildung. Auch verschiedene Bildschirmauflösungen wurden letztlich nur linear abgebildet.
Suchmaschinen nutzen Pageranks einer Website, um ihre Suchergebnisse zu sortieren. „Mathe für Nicht-Freaks“, eine zufällige Seite aus dem Internet, erhält so zum Beispiel ein Ranking. Um den Pagerank einer Seite zu bestimmen, wird eine sogenannte Markov-Kette verwendet, die wiederum eine lineare Abbildung ist.