Teil B

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe-Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
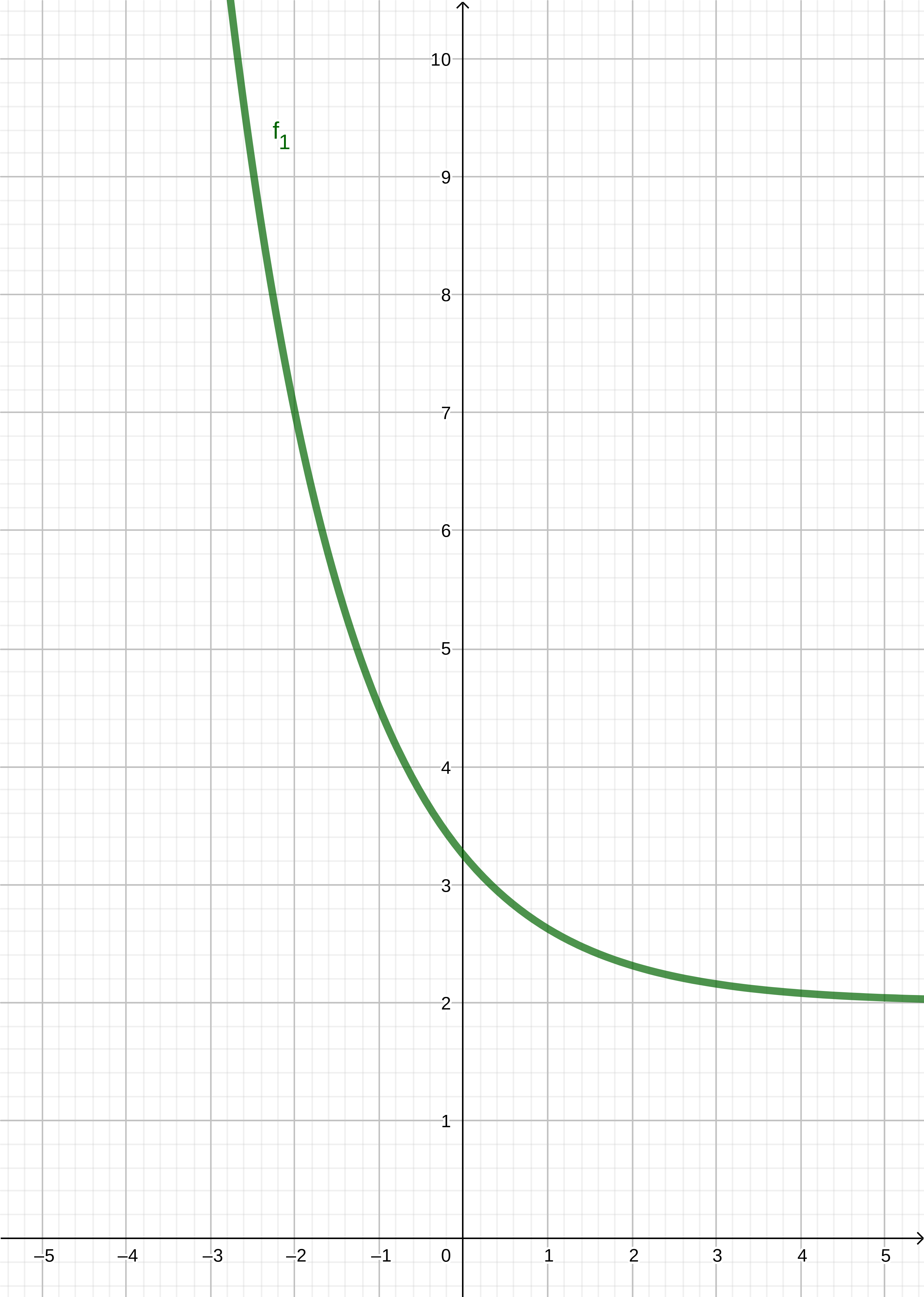
Gegeben ist die Funktion $f_{1}$ mit der Gleichung $y = 10 \cdot {0,5}^{x + 3} + 2$
$(𝔾 = ℝ \times ℝ)$
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
Geben Sie die Definitionsmenge der Funktion $f_{1}$ an.
Zeichnen Sie sodann den Graphen zu $f_{1}$ für $x \in [- 2,5; 5]$ in ein Koordinatensystem.
Für die Zeichnung: Längeneinheit $1 cm$ ; $- 5 ⩽ x ⩽ 5$ ; $- 6 ⩽ y ⩽ 10$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktionen
Die Definitionsmenge der Funktion beinhaltet alle Zahlen, die in die Funktion eingesetzt werden dürfen.
$0,5$ ist eine positive Zahl, im Exponenten kann daher eine beliebige Zahl eingesetzt werden. Die Definitionsmenge von $f_{1}$ sind dementsprechend die reellen Zahlen $ℝ$ .
$𝔻 = ℝ$
Der Graph von $f_{1}$ sieht so aus:

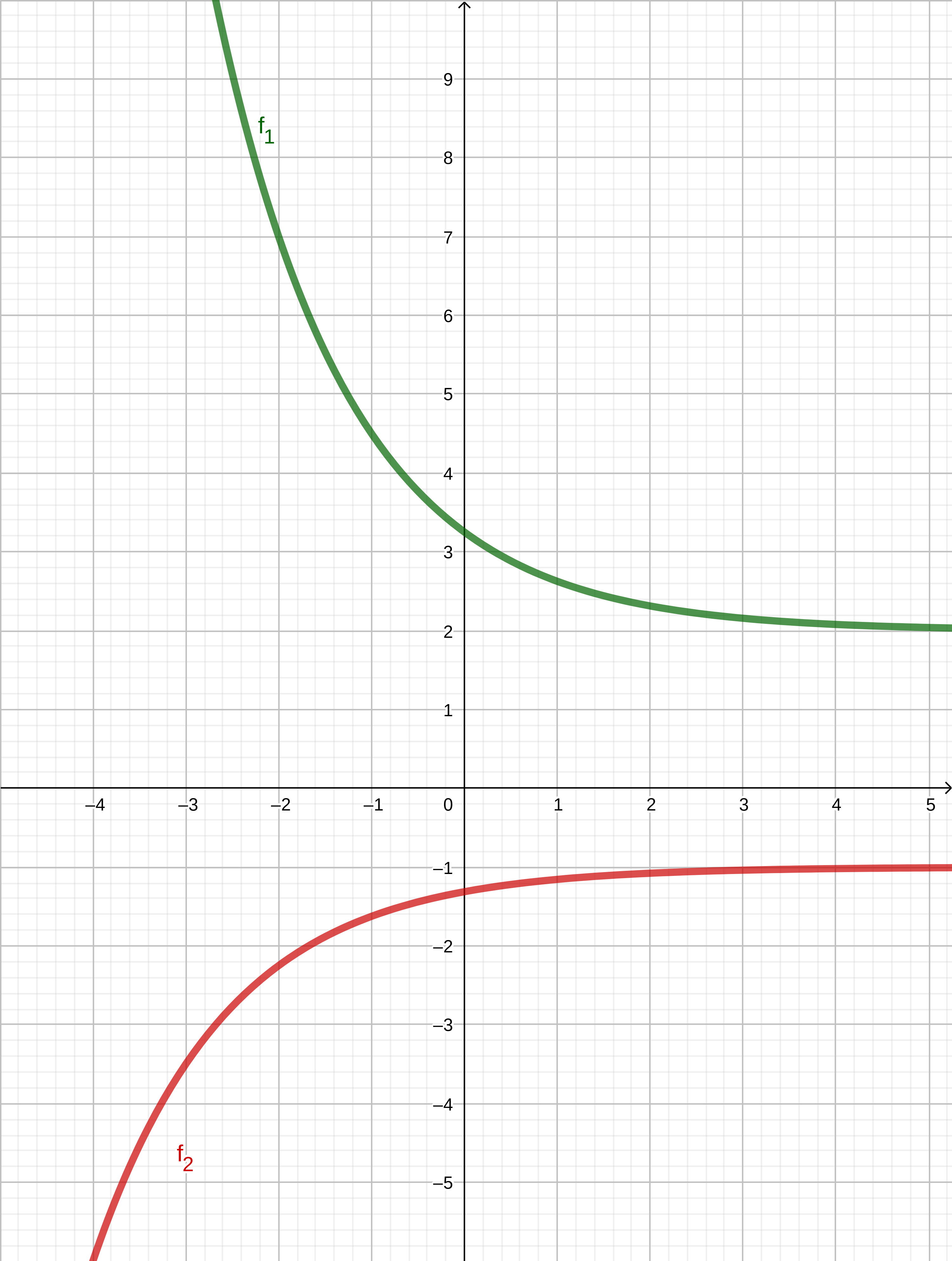
Der Graph der Funktion $f_{1}$ wird durch Achsenspiegelung an der x-Achse sowie anschließende Parallelverschiebung mit dem Vektor $\vec{v} = (\begin{array}{c} - 2 \\ 1 \end{array})$ auf den Graphen der Funktion $f_{2}$ abgebildet.
Zeigen Sie rechnerisch, dass die Funktion $f_{2}$ die Gleichung $y = - 10 \cdot {0,5}^{x + 5} - 1$ mit $𝔾 = ℝ \times ℝ$ besitzt.
Geben Sie sodann die Gleichung ihrer Asymptote an und zeichnen Sie den Graphen zu $f_{2}$ $x \in [- 4; 5]$ in das Koordinatensystem zu Teilaufgabe a) ein.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktionen
Hier geht es zunächst darum, eine Funktion erst zu spiegeln und danach zu verschieben.
Schritt 1: Spiegelung an der x-Achse
Um $f_{1}$ an der x-Achse zu spiegeln, multiplizierst du den Funktionsterm mit $- 1$ :
$(- 1) \cdot (10 \cdot {0,5}^{x + 3} + 2) = - 10 \cdot {0,5}^{x + 3} - 2$
Schritt 2: Parallelverschiebung
Nun musst du die Funktion noch mit dem Vektor $\vec{v} = (\begin{array}{c} - 2 \\ 1 \end{array})$ verschieben. Der Vektor verschiebt $f_{1}$ um $- 2$ in x-Richtung, also erhältst du $f_{1} (x + 2)$ , und um $1$ in y-Richtung, diese Verschiebung bekommst du durch $f_{1} (x) + 1$ . Insgesamt entsteht also als Funktionsterm:
$f_{2} (x) = - 10 \cdot {0,5}^{(x + 2) + 3} - 2 + 1 = - 10 \cdot {0,5}^{x + 5} - 1$
Die Asymptote von $f_{2}$ liegt bei $y = - 1$ . Dafür kannst du dir das Verhalten der Funktion ansehen. Wenn $x$ sehr große Werte annimmt, dann geht der Term $- 10 \cdot {0,5}^{x + 5}$ gegen $0$ und die Funktion geht dann gegen $- 1$ .

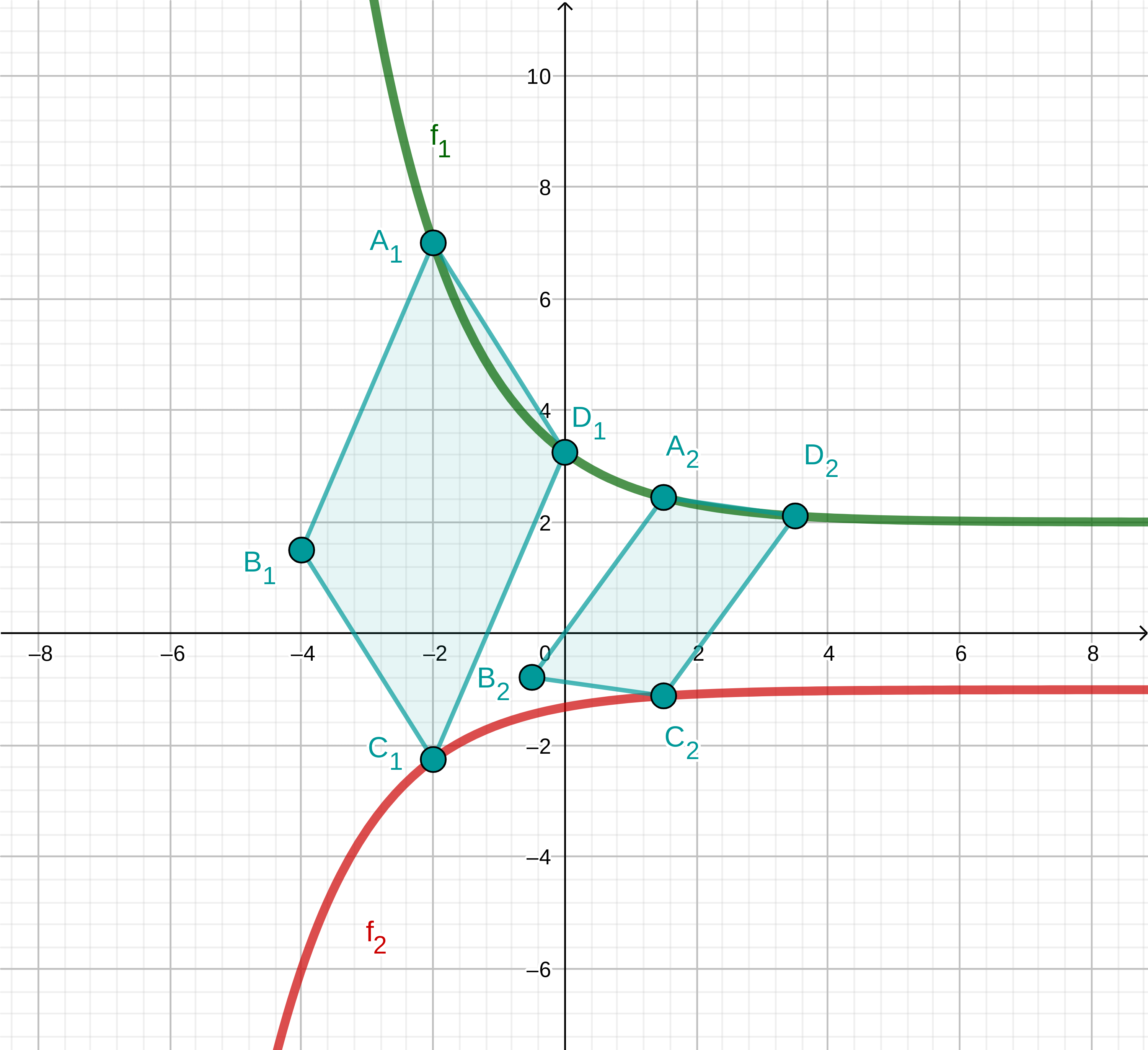
Punkte $A_{n} (x | 10 \cdot {0,5}^{x + 3} + 2)$ auf dem Graphen zu $f_{1}$ und Punkte $C_{n} (x | - 10 \cdot {0,5}^{x + 5} - 1)$ auf dem Graphen zu $f_{2}$ haben dieselbe Abszisse $x$ und sind zusammen mit Punkten $B_{n}$ und $D_{n}$ die Eckpunkte von Parallelogrammen $A_{n} B_{n} C_{n} D_{n}$ .
Die Punkte $D_{n}$ liegen ebenfalls auf dem Graphen zu $f_{1}$ , ihre Abszisse ist um $2$ größer als die Abszisse $x$ der Punkte $A_{n}$ .
Zeichnen Sie die Parallelogramme $A_{1} B_{1} C_{1} D_{1}$ für $x = - 2$ und $A_{2} B_{2} C_{2} D_{2}$ für $x = 1,5$ in das Koordinatensystem zu Teilaufgabe a) ein.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktionen
Bei dieser Teilaufgabe musst du die Koordinaten der Punkte nicht ausrechnen, um die Parallelogramme einzuzeichnen. Trotzdem kannst du dir hier nochmal rechnerisch veranschaulichen, wie die Punkte entstehen.
Bereits gegeben sind die Koordinaten der Punkte
$A_{n} (x | 10 \cdot {0,5}^{x + 3} + 2) auf f_{1}$
und
$C_{n} (x | - 10 \cdot {0,5}^{x + 5} - 1) auf f_{2} .$
Die Koordinaten der Punkte $D_{n}$ bestimmt man durch Veränderung der Abszisse von $A_{n}$ (man rechnet lediglich $x + 2$ ).
$D_{n} (x + 2 | 10 \cdot {0,5}^{(x + 2) + 3} + 2)$
Für $x = - 2$ erhältst du also die Punkte $A_{1} (- 2 | 7)$ , $C_{1} (- 2 | - 2,25)$ und $D_{1} (0 | 3,25) .$ Die Koordinaten des Punktes $B_{1}$ erhältst du, indem du an den Punkt $C_{1}$ den Vektor $\vec{D_{1} A_{1}}$ anlegst. Es gilt dann:
$\vec{O B_{1}} = \vec{O C_{1}} + \vec{D_{1} A_{1}} = (\begin{array}{c} - 2 \\ - 2,25 \end{array}) + (\begin{array}{c} - 2 - 0 \\ 7 - 3,25 \end{array}) = (\begin{array}{c} - 4 \\ 1,5 \end{array})$
Die Koordinaten des Punktes sind also $B_{1} (- 4 | 1,5)$ .
Für $x = 1,5$ erhältst du die Punkte $A_{2} (1,5 | 2,44)$ , $C_{2} (1,5 | - 1,11)$ und $D_{2} (3,5 | 2,11)$ . Für $B_{2}$ gilt dann:
$\vec{O B_{1}} = \vec{O C_{1}} + \vec{D_{1} A_{1}} = (\begin{array}{c} 1,5 \\ - 1,11 \end{array}) + (\begin{array}{c} - 1,5 - 3,5 \\ 2,44 - 2,11 \end{array}) = (\begin{array}{c} - 0,5 \\ - 0,88 \end{array})$
Die Koordinaten sind diesmal also $B_{2} (- 0,5 | - 0,88) .$
Hinweis: auch ein Blick in Aufgabe e) liefert die Lösung für die Koordinaten der Punkte $B_{1 / 2}$ !

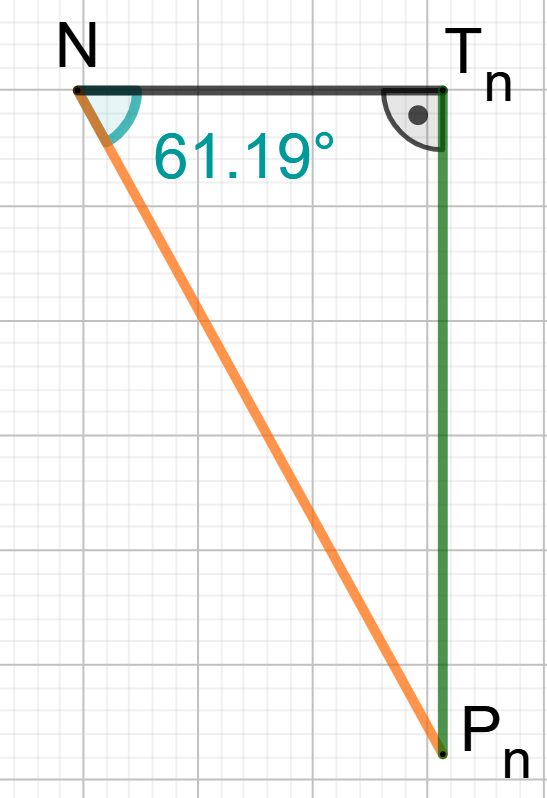
Berechnen Sie das Maß des Winkels $A_{1} D_{1} C_{1}$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktionen
Das Maß des Winkels $∠ A_{1} D_{1} C_{1}$ ist das Maß des Winkels $φ$ zwischen den Vektoren $\vec{D_{1} A_{1}}$ und $\vec{D_{1} C_{1}} .$ Um es zu berechnen benötigst du das Skalarprodukt.
Den Vektor $\vec{D_{1} A_{1}} = (\begin{array}{c} - 2 \\ 3,75 \end{array})$ hast du bereits in Teilaufgabe c) verwendet. Nun kannst du noch $\vec{D_{1} C_{1}} = \vec{O C_{1}} - \vec{O D_{1}} = (\begin{array}{c} - 2 \\ - 5,5 \end{array})$ berechnen. Eingesetzt in die Formel für die Berechnung des Winkels zwischen zwei Vektoren erhältst du:
$\cos (φ) = \frac{(\begin{array}{c} - 2 \\ 3,75 \end{array}) ⊙ (\begin{array}{c} - 2 \\ - 5,5 \end{array})}{| \begin{array}{c} - 2 \\ 3,75 \end{array} | \cdot | \begin{array}{c} - 2 \\ - 5,5 \end{array} |} = \frac{(- 2) \cdot (- 2) + 3,75 \cdot (- 5,5)}{(\sqrt{4 + {3,75}^{2}}) \cdot (\sqrt{4 + {5,5}^{2}})}$
Das Ergebnis ist dann $\cos (φ) = - 0,6684$ . Durch Anwendung des Arkuskosinus erhältst du nun das Endergebnis $φ = {131,94}^{\circ}$ .

Zeigen Sie rechnerisch, dass für die Koordinaten der Punkte $B_{n}$ in Abhängigkeit von der Abszisse $x$ der Punkte $A_{n}$ gilt:
$B_{n} (x - 2 | 5 \cdot {0,5}^{x + 3} - 1)$
[Teilergebnis: $D_{n} (x + 2 | 10 \cdot {0,5}^{x + 5} + 2)]$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktionen
Bei dieser Aufgabe sind die Potenzgesetze wichtig.
Wie du schon aus Teilaufgabe c) weißt, erhältst du die Punkte $B_{n}$ indem du den Vektor $\vec{D_{n} A_{n}}$ an den Punkt $C_{1}$ anlegst. Nun kannst du zuerst die Koordinaten von $\vec{D_{n} A_{n}}$ bestimmen:
$\vec{D_{n} A_{n}} = \vec{O A_{n}} - \vec{O D_{n}} = (\begin{array}{c} x - (x + 2) \\ 10 \cdot {0,5}^{x + 3} + 2 - (10 \cdot {0,5}^{x + 5} + 2) \end{array})$
Unter Verwendung der Potenzgesetze gilt nun
${0,5}^{x + 5} = {0,5}^{x + 3 + 2} = {0,5}^{x + 3} \cdot {0,5}^{2} = {0,5}^{x + 3} \cdot 0,25 .$
Du erhältst dann für $\vec{D_{n} A_{n}} :$
$\begin{array}{rcl} \vec{D_{n} A_{n}} & = & (\begin{array}{c} - 2 \\ 10 \cdot {0,5}^{x + 3} + 2 - (10 \cdot 0,25 \cdot {0,5}^{x + 3} + 2) \end{array}) \\ = & (\begin{array}{c} - 2 \\ 10 \cdot {0,5}^{x + 3} + 2 - 10 \cdot 0,25 \cdot {0,5}^{x + 3} - 2 \end{array}) \\ = & (\begin{array}{c} - 2 \\ 10 \cdot {0,5}^{x + 3} + 2 - 2,5 \cdot {0,5}^{x + 3} - 2 \end{array}) \\ \vec{D_{n} A_{n}} & = & (\begin{array}{c} - 2 \\ 7,5 \cdot {0,5}^{x + 3} \end{array}) \end{array}$
Jetzt kannst du $B_{n}$ bestimmen:
$\begin{array}{rcl} \vec{O B_{n}} & = & \vec{O C_{n}} + \vec{D_{n} A_{n}} \\ = & (\begin{array}{c} x - 2 \\ - 10 \cdot {0,5}^{x + 5} - 1 + 7,5 \cdot {0,5}^{x + 3} \end{array}) \\ = & (\begin{array}{c} x - 2 \\ - 10 \cdot 0,25 \cdot {0,5}^{x + 3} - 1 + 7,5 \cdot {0,5}^{x + 3} \end{array}) \\ = & (\begin{array}{c} x - 2 \\ - 2,5 \cdot {0,5}^{x + 3} - 1 + 7,5 \cdot {0,5}^{x + 3} \end{array}) \\ \vec{O B_{n}} & = & (\begin{array}{c} x - 2 \\ 5 \cdot {0,5}^{x + 3} - 1 \end{array}) \end{array}$
Insgesamt erhältst du also: $B_{n} (x - 2 | 5 \cdot {0,5}^{x + 3} - 1)$ .

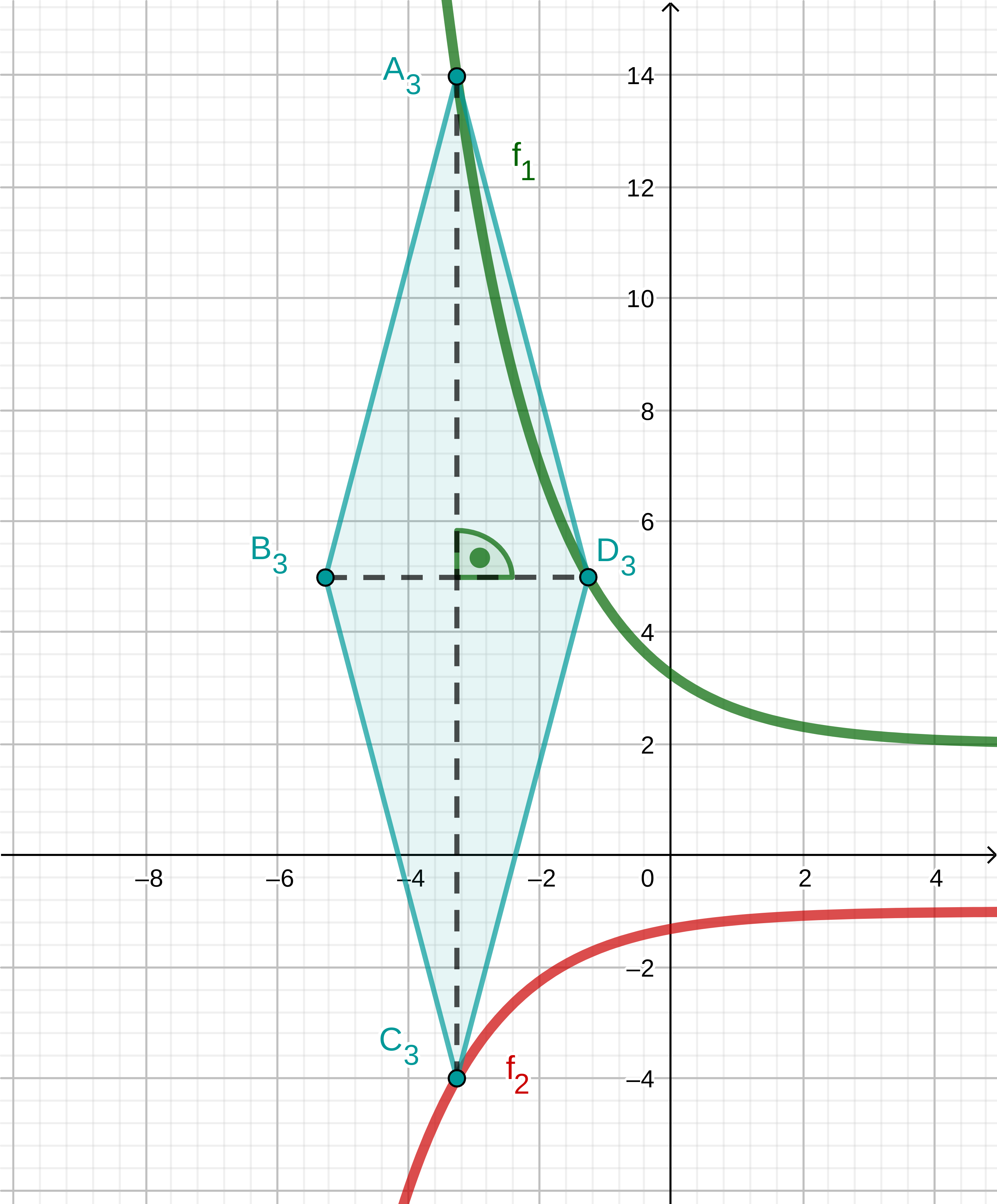
Unter den Parallelogrammen $A_{n} B_{n} C_{n} D_{n}$ gibt es die Raute $A_{3} B_{3} C_{3} D_{3}$ . Berechnen Sie die x-Koordinate des Punktes $A_{3}$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktion
Bei einer Raute sind alle Seiten gleich lang. Außerdem stehen die Diagonalen der Raute senkrecht aufeinander.
Die Diagonalen von $A_{3} B_{3} C_{3} D_{3}$ sind $\vec{A_{3} C_{3}}$ und $\vec{B_{3} D_{3}}$ .
$\vec{A_{3} C_{3}}$ verläuft parallel zur y-Achse (gleiche Abszisse x), deshalb verläuft $\vec{B_{3} D_{3}}$ parallel zur x-Achse.
Die y-Werte von $B_{3}$ und $D_{3}$ sind also gleich und du erhältst diese Gleichung:
$\begin{array}{rcrcl} y_{B_{3}} & = & y_{D_{3}} \\ 5 \cdot {0,5}^{x + 3} - 1 & = & 10 \cdot {0,5}^{x + 5} + 2 \\ 5 \cdot {0,5}^{x + 3} & - & 10 \cdot {0,5}^{x + 5} & = & 3 \\ 5 \cdot {0,5}^{x + 3} & - & 10 \cdot 0,25 \cdot {0,5}^{x + 3} & = & 3 \\ 5 \cdot {0,5}^{x + 3} & - & 2,5 \cdot {0,5}^{x + 3} & = & 3 \\ 2,5 \cdot {0,5}^{x + 3} & = & 3 \end{array}$
Um diese Gleichung zu lösen, wendest du jetzt noch den Logarithmus auf beide Seiten der Gleichung an und verwendest seine Gesetze:
$\begin{array}{c} \ln (2, 5 \cdot {0,5}^{x + 3}) & = & \ln (3) \\ \ln (2,5) + (x + 3) \cdot \ln (0,5) & = & \ln (3) \\ (x + 3) \cdot \ln (0,5) & = & \ln (3) - \ln (2,5) \\ x + 3 & = & \frac{\ln (3) - \ln (2,5)}{\ln (0,5)} \\ x & = & \frac{\ln (3) - \ln (2,5)}{\ln (0,5)} - 3 \end{array}$
$𝕃 = {- 3,26}$
Die Abszisse von $A_{3}$ ist also $x = - 3,26$ .
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
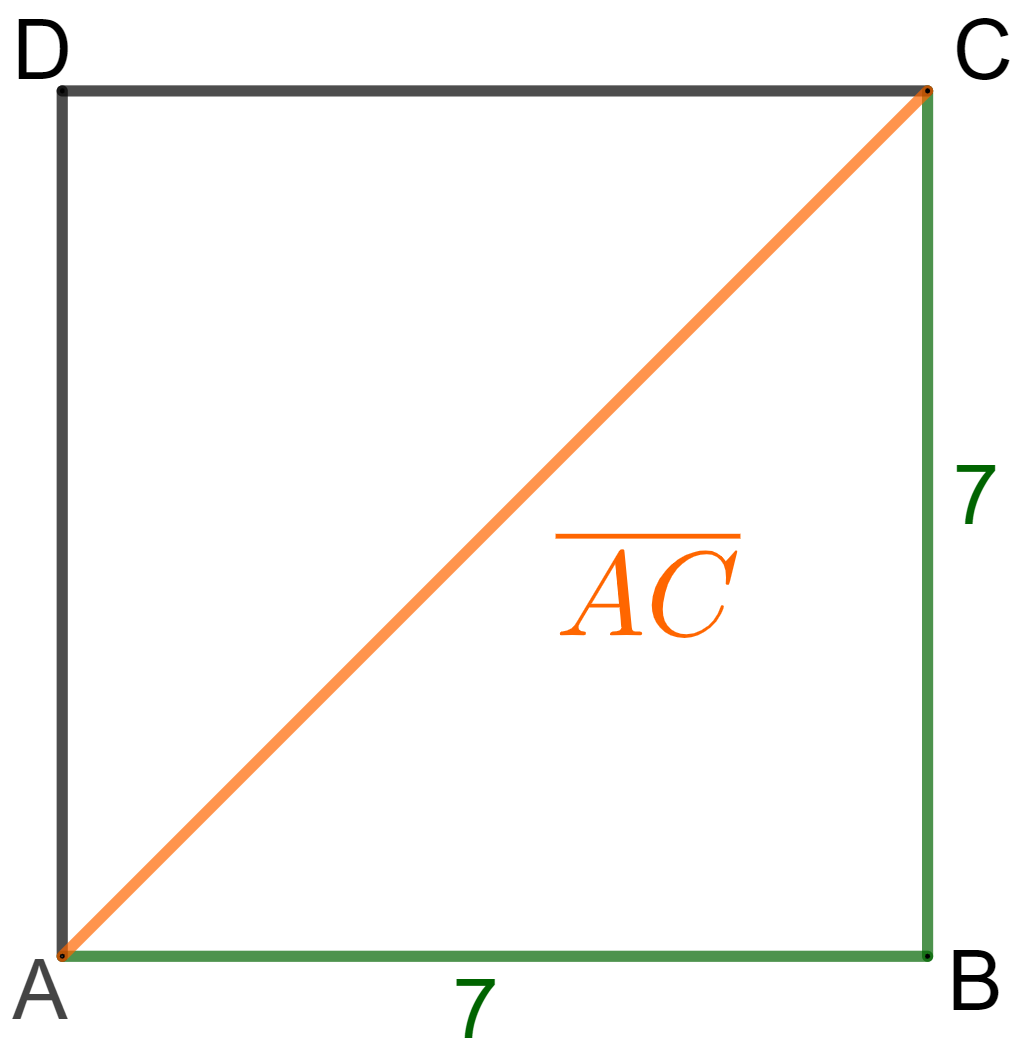
Das Quadrat $A B C D$ mit dem Diagonalenschnittpunkt $M$ ist die Grundfläche des geraden Prismas $A B C D E F G H$ mit der Höhe $[A E]$ . Der Schnittpunkt der Diagonalen $[E G]$ und $[F H]$ des Quadrats $E F G H$ ist der Punkt $N$ .
Es gilt $A B = 7 cm; A E = 9 cm$ .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
Zeigen Sie, dass für die Länge der Strecke $[A C]$ gilt: $A C = 9,90 cm$ .
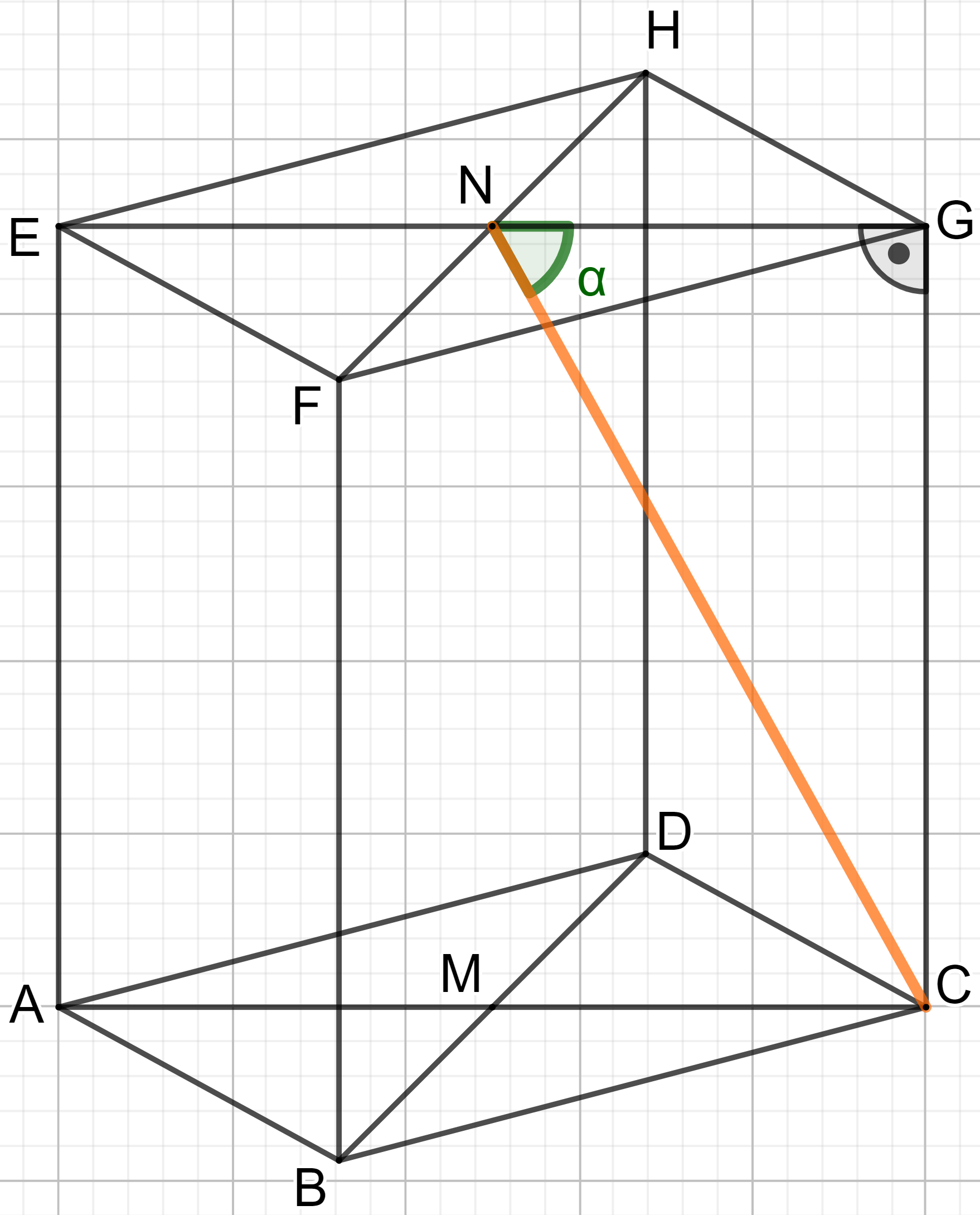
Zeichnen Sie sodann das Schrägbild des Prismas $A B C D E F G H$ , wobei die Strecke $A C$ auf der Schrägbildachse und der Punkt $A$ links vom Punkt $C$ liegen soll.
Für die Zeichnung gilt: $q = \frac{1}{2}; ω = 45^{\circ}$

Außerdem benötigst du folgendes Grundwissen: Zeichnen eines Schrägbilds
Die Strecke $[AC]$ ist eine Diagonale im Quadrat $A B C D$ . Das Quadrat hat die Seitenlänge $A B = 7 cm$ . Mit dem Satz des Pythagoras gilt dann:
$\begin{array}{ccl} \orange {A C}^{2} & = & {(\green 7 cm)}^{2} + {(\green 7 cm)}^{2} \\ {A C}^{2} & = & 98 {cm}^{2} | \sqrt{} \\ A C & = & \pm 9,90 cm \end{array}$
Da eine Seitenlänge nicht negativ sein kann, ist das richtige Ergebnis $A C = 9,90 cm$ .
Nun musst du noch das Schrägbild des Prismas zeichnen, wie du das machst, kannst du dir im folgenden Applet ansehen. Hilfreich für dich ist es dabei zu wissen, dass die Strecke $[BD]$ dieselbe Länge wie $[AC]$ , also $9,90 cm$ , hat.
Klicke auf den angezeigten Satz!
Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unsererDatenschutzerklärung.

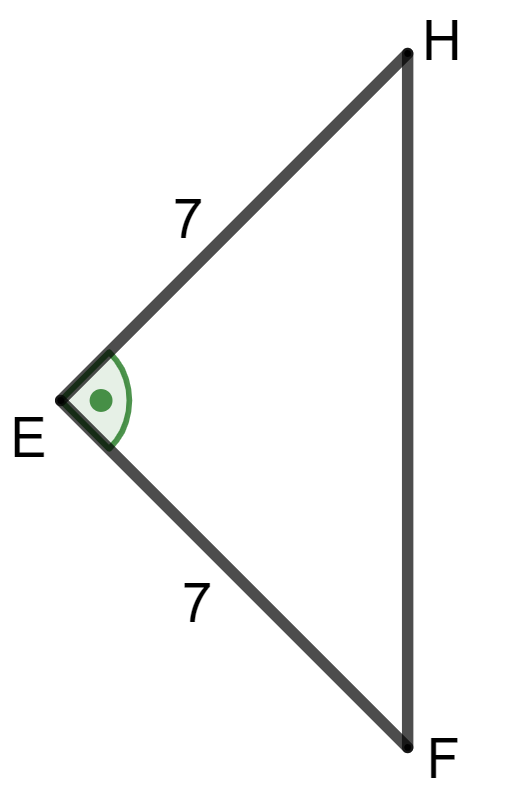
Berechnen Sie die Länge der Strecke $[C N]$ sowie das Maß des Winkels $C N G$ .
[Ergebnis: $∢ C N G = {61,19}^{\circ}$ ]

Außerdem benötigst du folgendes Grundwissen: Satz des Pythagoras
Um die Seitenlänge $C N$ zu berechnen, kannst du das rechtwinklige Dreieck $C G N$ betrachten, in dem $[C N]$ die Hypotenuse ist. Die Seitenlängen der Katheten $C G = A E = 9 cm$ und $N G = 0,5 \cdot A C = 4,95 cm$ kennst du bereits. Also kannst du den Satz des Pythagoras verwenden und erhältst:
$\begin{array}{lcl} {C N}^{2} & = & {(4,95 cm)}^{2} + {(9 cm)}^{2} \\ {C N}^{2} & = & 105,50 {cm}^{2} | \sqrt{} \\ C N & = & 10,27 cm \end{array}$
Die Strecke $[C N]$ ist also $10,27 cm$ lang.
Jetzt sollst du noch das Maß des Winkels $∢ C N G$ berechnen, im Bild oben ist er als $\green α$ eingezeichnet. Auch er liegt im Dreieck $C G N$ . Von ihm aus gesehen ist $[C G]$ die Gegenkathete und $[N G]$ die Ankathete. Mit dem Tangens gilt:
$\begin{array}{ccl} \tan (α) & = & \frac{Gegenkathete}{Ankathete} = \frac{9 cm}{4,95 cm} \\ \tan (α) & = & 1,8182 \end{array}$
Wenn du darauf nun die Umkehrfunktion des Tangens anwendest, erhältst du das Ergebnis: $α = \tan^{- 1} (1,8182) = 61,19 °$ .

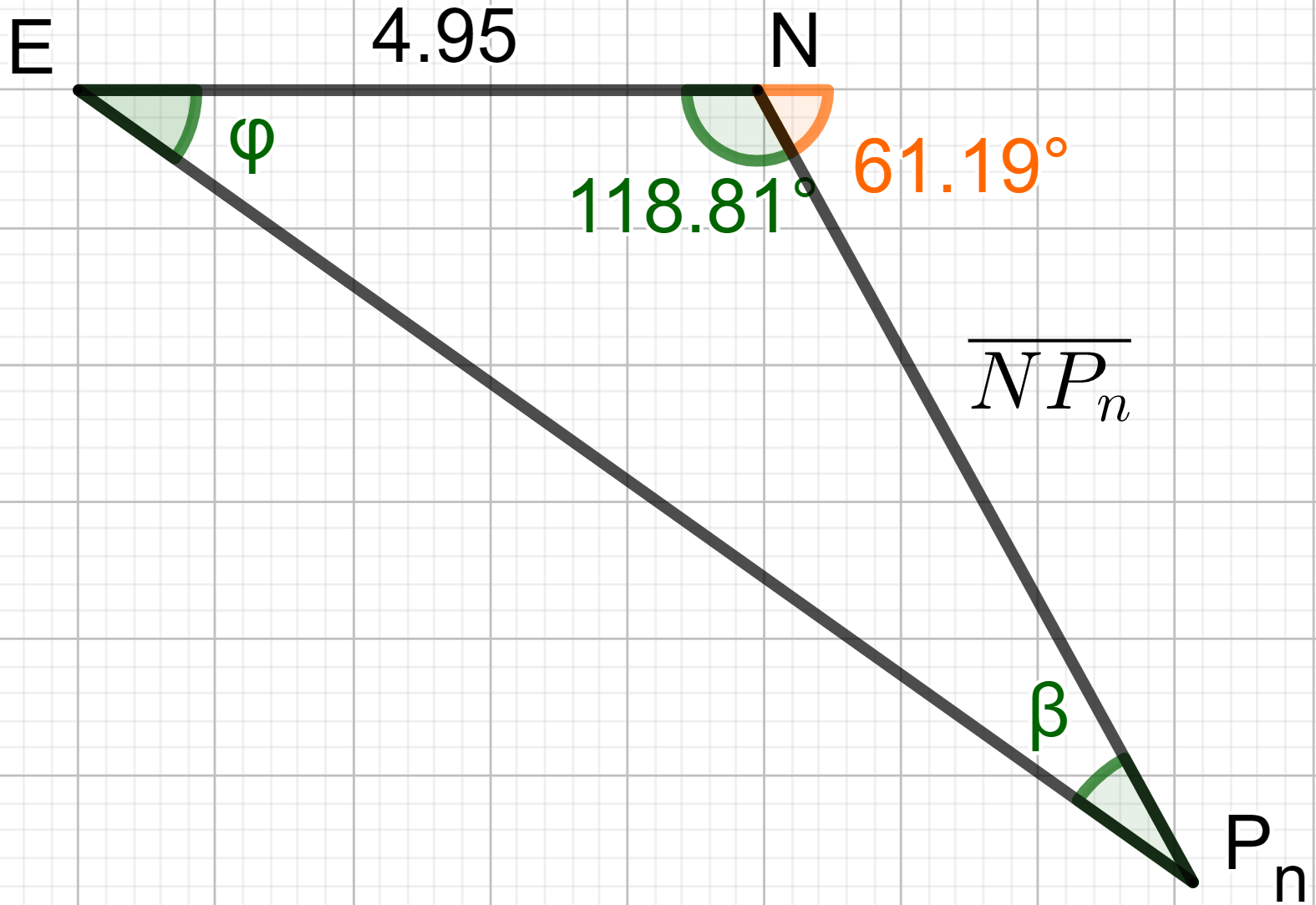
Die Punkte $P_{n}$ liegen auf der Strecke $[C N] .$ Die Winkel $P_{n} E N$ haben das Maß $φ$ mit $φ \in] 0; {42,27}^{\circ}]$ . Die Punkte $P_{n}$ sind zusammen mit den Punkten $N$ und $E$ die Eckpunkte von Dreiecken $P_{n} N E$ .
Zeichnen Sie das Dreieck $P_{1} N E$ für $φ = 38^{\circ}$ in das Schrägbild zu Teilaufgabe a) ein und begründen Sie sodann die obere Intervallgrenze für $φ$ .

Zuerst solltest du das Dreieck $P_{1} N E$ einzeichnen, wie das aussieht, kannst du im folgenden Applet sehen. Außerdem kannst du den Punkt $P$ auf der Strecke $[C N]$ bewegen und dir ansehen, welche Werte der Winkel $φ$ annimmt:
Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unsererDatenschutzerklärung.
Nun musst du noch die obere Intervallgrenze für $φ$ begründen.
Das Maß des Winkels $φ$ wird größer, je näher der Punkt $P_{n}$ am Punkt $C$ ist. $φ$ ist also am größten, wenn $P_{n}$ auf $C$ liegt, $φ$ entspricht dann dem Winkel $∢ C E G$ , dieser liegt im rechtwinkligen Dreieck $C G E$ . Du kannst also den Tangens verwenden, um das Maß des Winkels zu berechnen:
$\begin{array}{c} \tan (φ_{max}) & = & \frac{Gegenkathete}{Ankathete} & = & \frac{C G}{E G} \\ = & \frac{9 cm}{9,90 cm} & = & 0,9091 \end{array}$
Mit der Umkehrfunktion des Tangens erhältst du das Ergebnis:
$φ_{max} = \tan^{- 1} (0,9091) = 42,27 °$ .
Das Maß des Winkels $φ$ nimmt also maximal den Wert $42,27 °$ an.

Zeigen Sie durch Rechnung, dass für die Länge der Strecken $[N P_{n}]$ in Abhängigkeit von $φ$ gilt:
$N P_{n} (φ) = \frac{4,95 \cdot \sin (φ)}{\sin (φ + {118,81}^{\circ})} cm .$

Für diese Aufgabe verwendest du den Sinussatz im Dreieck $P_{n} N E$ .
Um den Sinussatz anwenden zu können, brauchst du zwei Winkel und die Längen der gegenüberliegenden Seiten. Du suchst die Länge $N P_{n}$ , der gegenüberliegende Winkel ist $φ$ . Außerdem kennst du den Wert der Länge $E N = 0,5 \cdot E G = 4,95 cm$ , der gegenüberliegende Winkel ist hier $β$ . Mit dem Sinussatz gilt dann also:
$\begin{array}{ccc} \frac{N P_{n}}{\sin (φ)} & = & \frac{4,95 cm}{\sin (β)} & | & \cdot \sin (φ) \\ N P_{n} & = & \frac{4,95 \cdot \sin (φ)}{\sin (β)} \end{array}$
Du musst jetzt also nur noch das Maß von $β$ bestimmen und dann in die Gleichung einsetzen. Die Winkelsumme in einem Dreieck beträgt immer $180 °$ . Es gilt also:
$β = 180 ° - φ - ∢ E N P_{n}$ . Der Winkel $∢ E N P_{n}$ ergibt zusammen mit dem Winkel $∢ C N G = 61,19 °$ eine Gerade, also einen $180 °$ Winkel, das kannst du nutzen, um sein Maß zu berechnen: $∢ E N P_{n} = 180 ° - 61,19 ° = 118,81 °$ .
Das kannst du nun in die Gleichung von oben einsetzen:
$N P_{n} = \frac{4,95 \cdot \sin (φ)}{\sin (180 ° - φ - 118,81 °)} = \frac{4,95 \cdot \sin (φ)}{\sin (180 ° - (φ + 118,81 °))}$
Mit der Formel $\sin (180 ° - γ) = \sin (γ)$ gilt also nun das, was du zeigen sollst:
$N P_{n} = \frac{4,95 \cdot \sin (φ)}{\sin (φ + 118,81 °)}$

Die Punkte $P_{n}$ sind die Spitzen von Pyramiden $E F H P_{n}$ mit den Höhen $[P_{n} T_{n}]$ , deren Fußpunkte $T_{n}$ auf der Strecke $[E G]$ liegen.
Zeichnen die Pyramide $E F H P_{1}$ und ihre Höhe $[P_{1} T_{1}]$ in das Schrägbild zu Teilaufgabe a) ein und ermitteln Sie sodann rechnerisch das Volumen $V$ der Pyramiden $E F H P_{n}$ in Abhängigkeit von $φ$ .
[Teilergebnis: $P_{n} T_{n} (φ) = \frac{4,34 \cdot \sin (φ)}{\sin (φ + {118,81}^{\circ})} cm$ ]

In dieser Aufgabe musst du das Volumen der Pyramide $E F H P_{n}$ berechnen.
Um das Volumen von $E F H P_{n}$ zu bestimmen, benötigst du den Flächeninhalt der Grundfläche $E F H$ und die Länge der Höhe $P_{n} T_{n}$ .
Die Fläche $E F H$ ist ein rechtwinkliges Dreieck. Die Grundseite hat die Länge $7 cm$ und die Höhe hat ebenfalls die Länge $7 cm$ .
Den Flächeninhalt kannst du nun mit der Formel berechnen:
$\begin{array}{rcl} A_{E F H} & = & \frac{1}{2} \cdot 7 cm \cdot 7 cm \\ = & 24,5 {cm}^{2} \end{array}$
Jetzt musst du nur noch die Länge der Strecke $P_{n} T_{n}$ berechnen, dafür betrachtest du das Dreieck $N P_{n} T_{n}$ :
Da das Dreieck rechtwinklig ist kannst du den Sinus verwenden und erhältst:
$\begin{array}{ccl} \underset{= 0,8762}{\underset{⏟}{\sin (61,19 °)}} & = & \frac{P_{n} T_{n}}{N P_{n}} | \cdot N P_{n} \\ N P_{n} \cdot \sin (61,19 °) & = & P_{n} T_{n} \end{array}$
Wenn du hier jetzt noch die Formel für $N P_{n}$ aus der Teilaufgabe d) einsetzt und ausmultiplizierst, erhältst du:
$P_{n} T_{n} (φ) = \frac{4,34 \cdot \sin (φ)}{\sin (φ + {118,81}^{\circ})} cm$
Nachdem du jetzt Grundfläche und Höhe berechnet hast, kannst du diese Ergebnisse in die Volumenformel der Pyramide einsetzen:
$\begin{array}{rcl} V_{E F H P_{n}} & = & \frac{1}{3} \cdot A_{E F H} \cdot P_{n} T_{n} = \frac{1}{3} \cdot 24,5 {cm}^{2} \cdot \frac{4,34 \cdot \sin (φ)}{\sin (φ + {118,81}^{\circ})} cm \\ = & \frac{35,44 \cdot \sin (φ)}{\sin (φ + {118,81}^{\circ})} {cm}^{3} \end{array}$

Die Punkte $P_{n}$ sind auch die Spitzen von Pyramiden $A B C D P_{n}$ .
Für die Pyramiden $E F H P_{2}$ und $A B C D P_{2}$ gilt:
$V_{E F H P_{2}} = V_{A B C D P_{2}} .$
Berechnen Sie den zugehörigen Wert für $φ$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumenformel
Du weißt, dass das Volumen der beiden Pyramiden gleich sein soll. In diese Gleichung kannst du nun die Volumenformel der Pyramide einsetzen und erhältst:
$\underset{= V_{E F H P_{2}}}{\underset{⏟}{\frac{1}{3} \cdot A_{E F H} \cdot P_{2} T_{2}}} = \underset{= V_{A B C D P_{2}}}{\underset{⏟}{\frac{1}{3} \cdot A_{A B C D} \cdot h_{A B C D}}}$
Das Ziel ist es jetzt diese Gleichung zuerst nach $P_{2} T_{2}$ aufzulösen, dann die Formel für den Wert dieser Strecke einzusetzen und anschließend $φ$ zu bestimmen.
Davor schaust du dir aber noch die anderen Teile der Gleichung an und setzt ein. Den Flächeninhalt der Grundfläche von $E F H$ : $A_{E F H} = 24,5 {cm}^{2}$ kennst du schon.
Den Flächeninhalt von $A B C D$ kannst du auch schnell berechnen. Es ist ein Quadrat mit der Seitenlänge $A B = 7 cm$ , der Flächeninhalt beträgt also:
$A_{A B C D} = {(7 cm)}^{2} = 49 {cm}^{2} .$
Die Höhen der beiden Pyramiden ergeben zusammen die Höhe des Prismas, es gilt also:
$9 cm = P_{2} T_{2} + h_{A B C D}$
Das kannst du umstellen und erhältst für die Höhe der unteren Pyramide: $h_{A B C D} = 9 cm - P_{2} T_{2}$ .
Jetzt kannst du wieder zur ursprünglichen Gleichung zurückkehren und alles einsetzen:
$\begin{array}{rclll} \frac{1}{3} \cdot 24,5 {cm}^{2} \cdot P_{2} T_{2} & = & \frac{1}{3} \cdot 49 {cm}^{2} \cdot (9 cm - P_{2} T_{2}) & | & \cdot 3 | : 49 {cm}^{2} \\ 0,5 \cdot P_{2} T_{2} & = & 9 cm - P_{2} T_{2} & | & + P_{2} T_{2} \\ 1,5 \cdot P_{2} T_{2} & = & 9 cm & | & : 1,5 \\ P_{2} T_{2} & = & 6 cm \end{array}$
Nun setzt du für $P_{2} T_{2}$ die Formel aus Teilaufgabe f) ein und löst nach $φ$ auf (Die Einheit $cm$ ist auf beiden Seiten gleich, du kannst sie also weglassen):
$\begin{array}{c} \frac{4,34 \cdot \sin (φ)}{\sin (φ + {118,81}^{\circ})} cm = 6 cm \end{array}$
Bei dieser Gleichung kannst du jetzt für den Sinus im Nenner das Additionstheorem verwenden:
$\frac{4,34 \cdot \sin (φ)}{\sin (φ) \cos ({118,81}^{\circ}) + \sin (118,81 °) \cos (φ)} = 6$
Hier kannst du jetzt beide Seiten der Gleichung mit dem Nenner der linken Seite multiplizieren:
$4,34 \cdot \sin (φ) = 6 \cdot \sin (φ) \cos ({118,81}^{\circ}) + 6 \cdot \sin (118,81 °) \cos (φ)$
Ziehe nun die $6 \cdot \sin (φ) \cos ({118,81}^{\circ})$ von der Gleichung ab:
$\begin{array}{rcl} 4,34 \cdot \sin (φ) - 6 \cdot \sin (φ) \cos ({118,81}^{\circ}) & = & 6 \cdot \sin (118,81 °) \cos (φ) \\ \sin (φ) \cdot (4,34 - 6 \cdot \cos ({118,81}^{\circ})) & = & 6 \cdot \sin (118,81 °) \cos (φ) \end{array}$
Hier teilst du nun durch $\cos (φ)$ und zusätzlich durch $(4,34 - 6 \cdot \cos ({118,81}^{\circ}))$ :
$\underset{= \tan (φ)}{\underset{⏟}{\frac{\sin (φ)}{\cos (φ)}}} = \frac{6 \cdot \sin (118,81 °)}{(4,34 - 6 \cdot \cos ({118,81}^{\circ}))}$
Den rechten Teil der Gleichung kannst du nun mit deinem Taschenrechner ausrechnen:
$\tan (φ) = 0,7270$
Mit der Umkehrfunktion des Tangens erhältst du jetzt als Endergebnis:
$φ = \tan^{- 1} (0,7270) = 36,02 °$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org