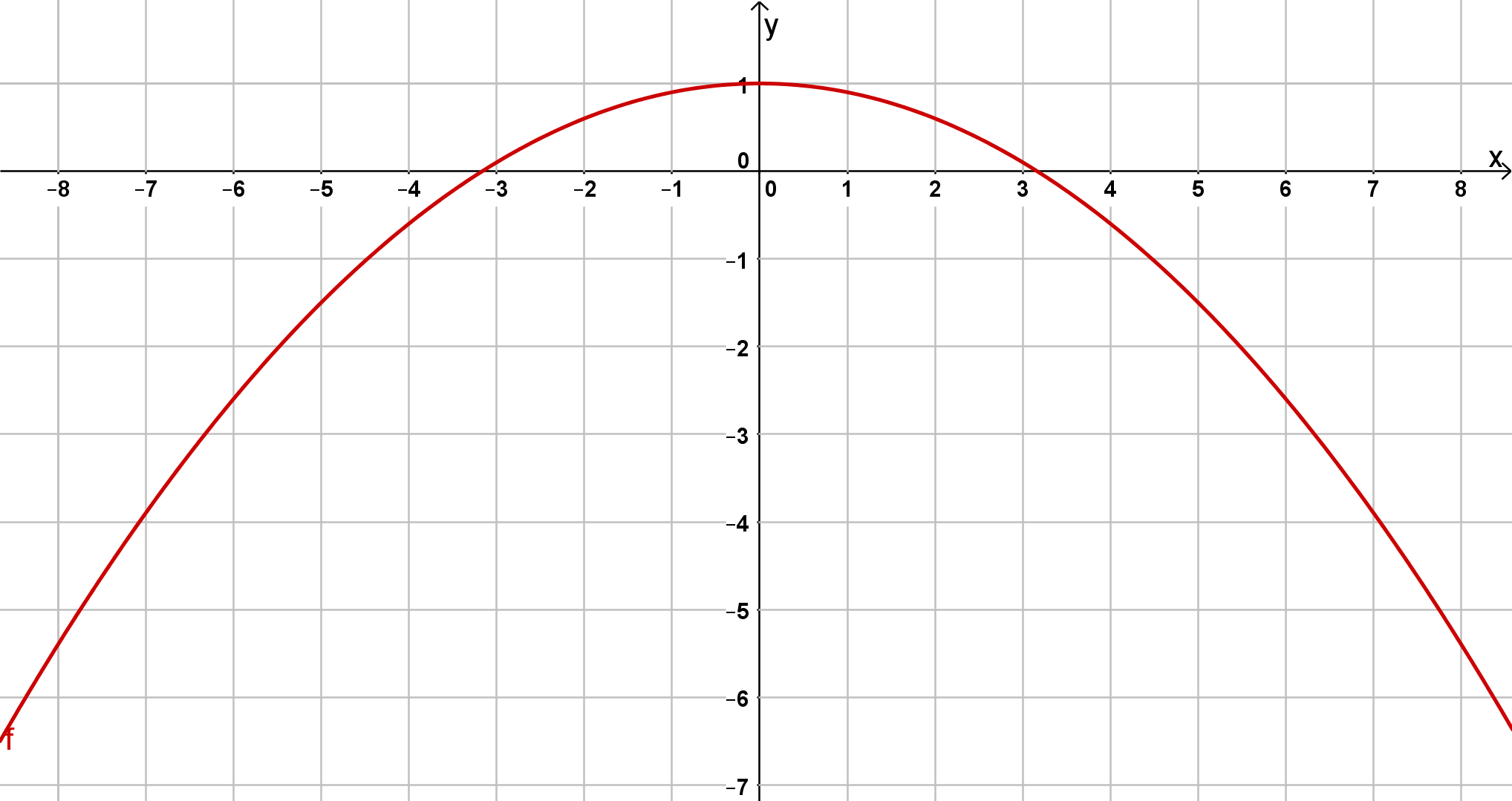
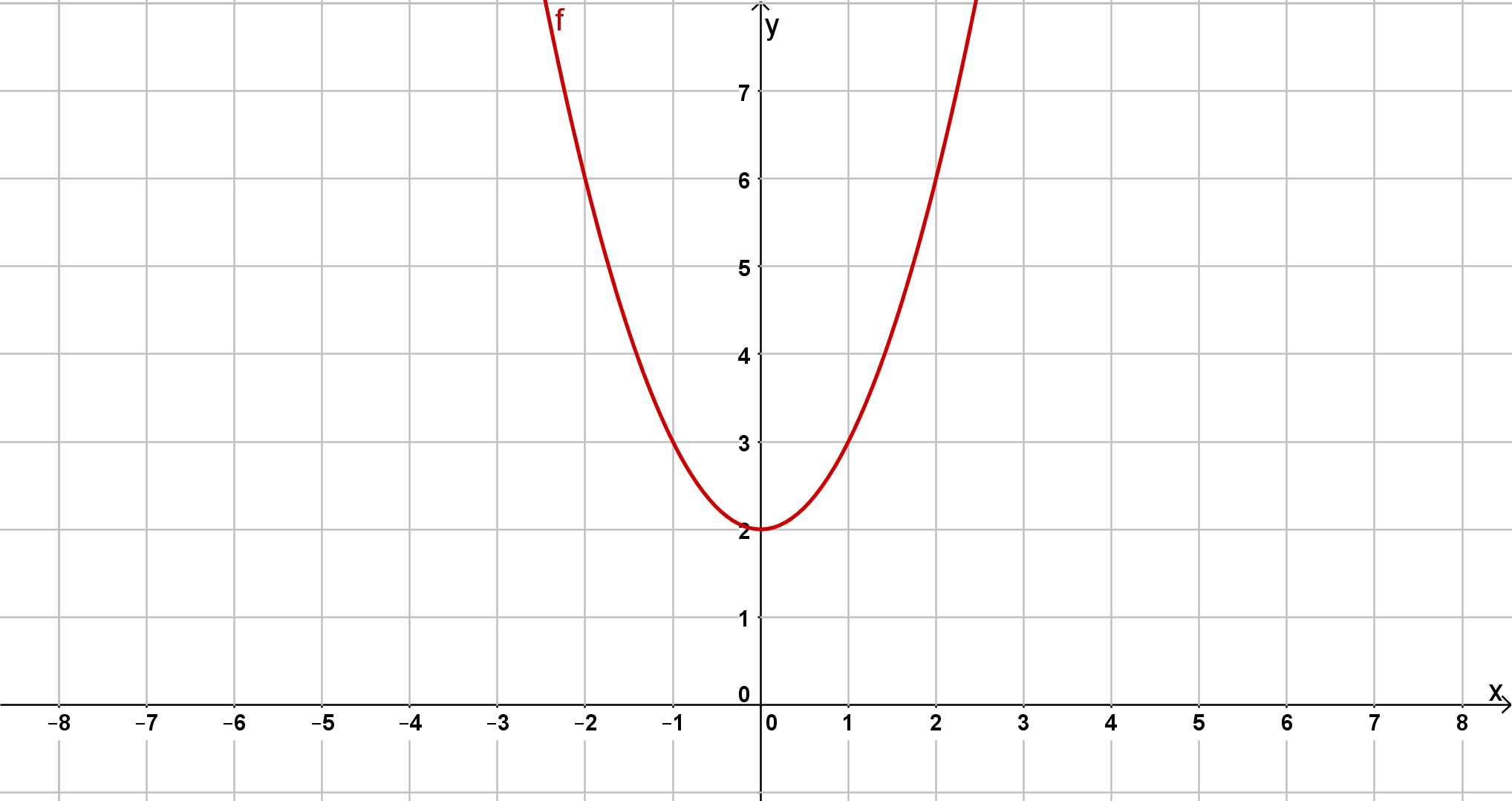
Aufgaben zu quadratischen Funktionen
- 1
Auf dem Graph der Funktion liegen die folgenden Punkte. Gib für jeden Punkt den Funktionsterm an.
- 2
Gib zu den jeweiligen Scheiteln von verschobenen Normalparabeln den Funktionsterm an.
- 3
Wie lautet die Gleichung einer nach unten geöffneten Normalparabel mit Scheitel ?
- 4
Bestimme die Funktionsgleichungen der quadratischen Funktionen mit den gegebenen Informationen.
Der Graph der Funktion verläuft durch die Punkte A(1|1), B(3|4), C(5|-1)
Die Funktion besitzt eine doppelte Nullstelle bei x=3 und geht durch den Punkt P(2|0,3).
Die nach unten geöffnete Normalparabel hat den Scheitelpunkt S(2|6).
Die Funktion hat den Scheitelpunkt S(0|-3) und geht durch den Punkt P(1,5|2).
Die Funktion geht durch die Punkte A(2|4), B(3|5), C(-1|13).
- 5
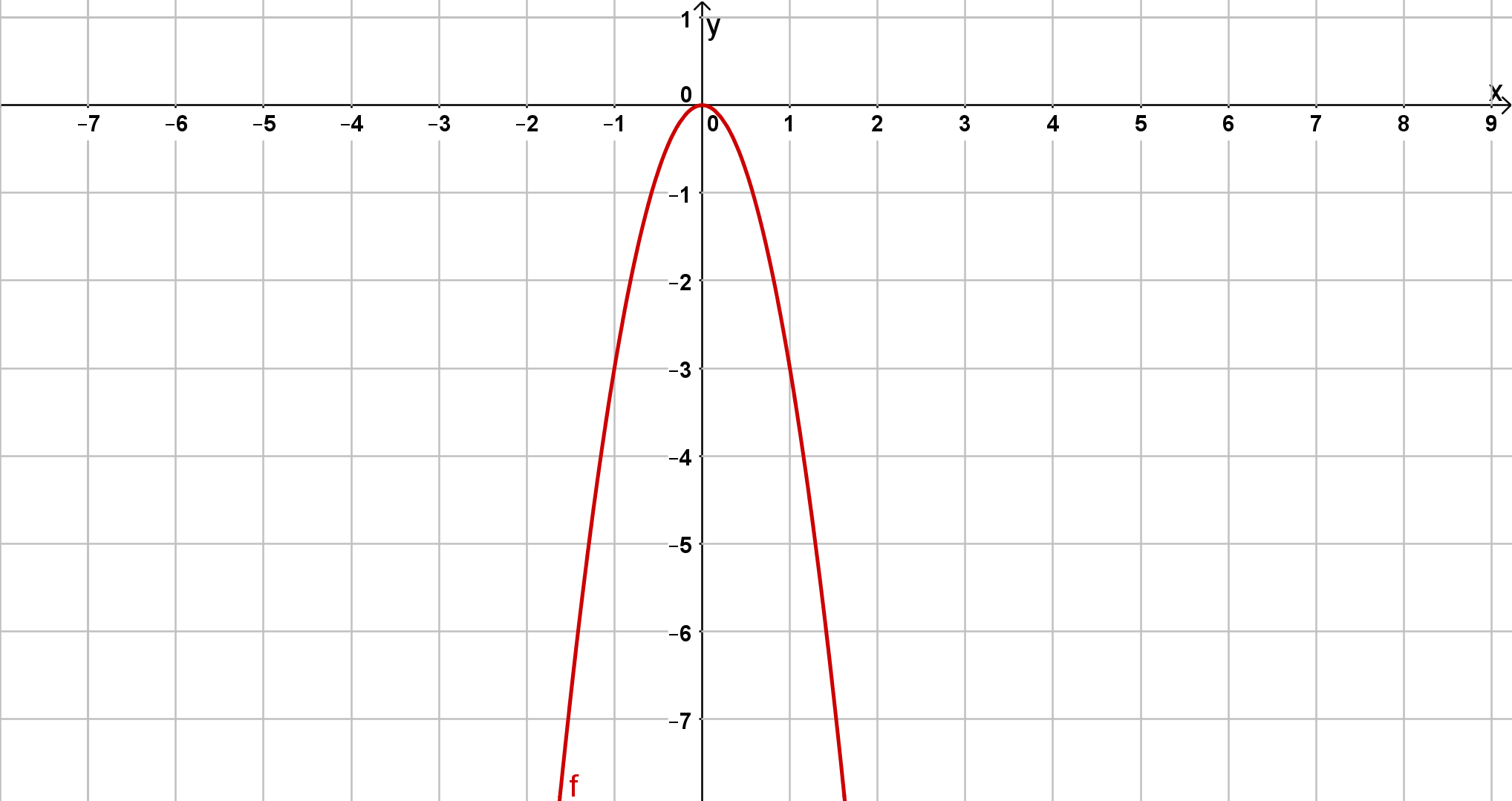
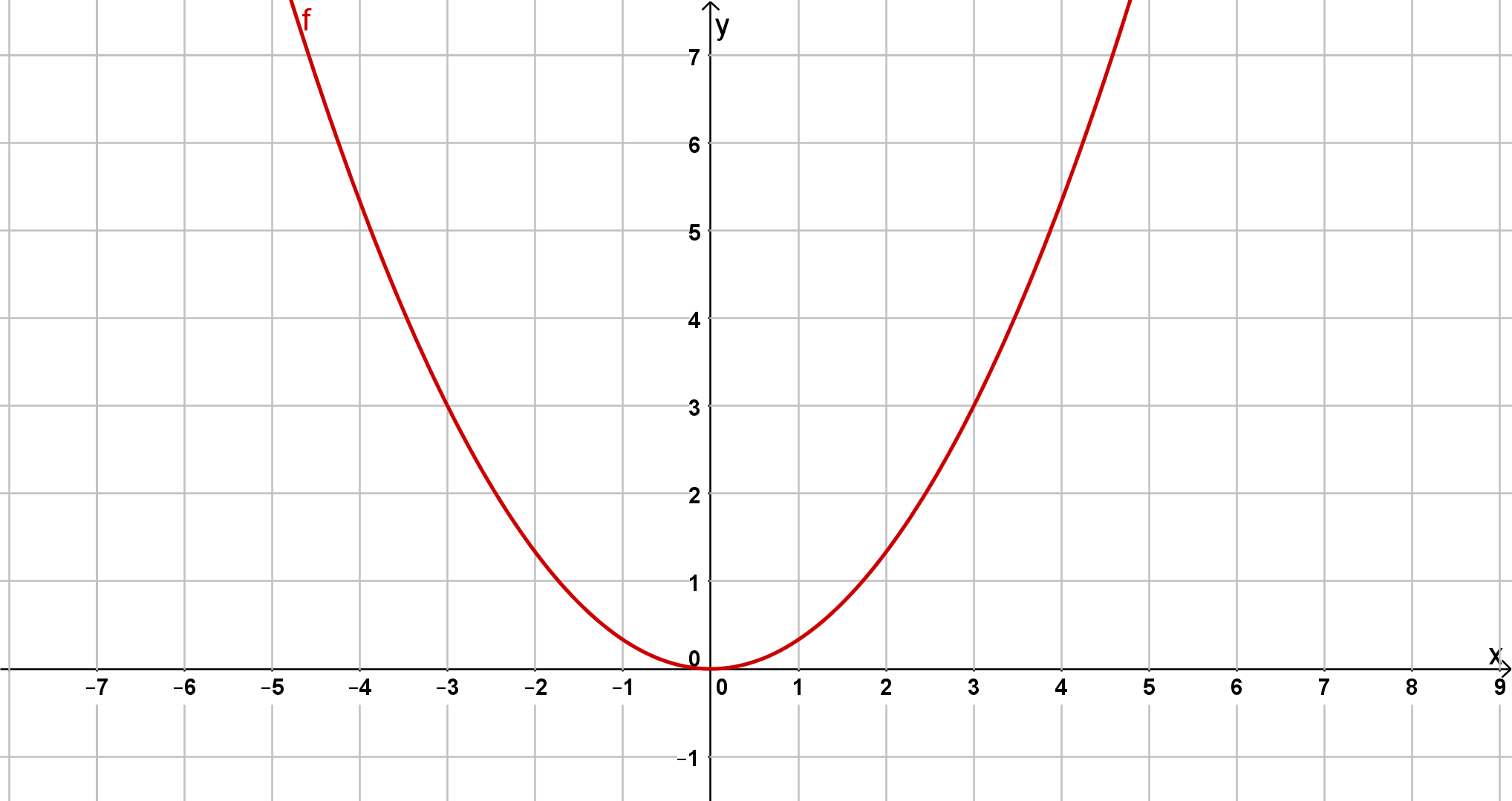
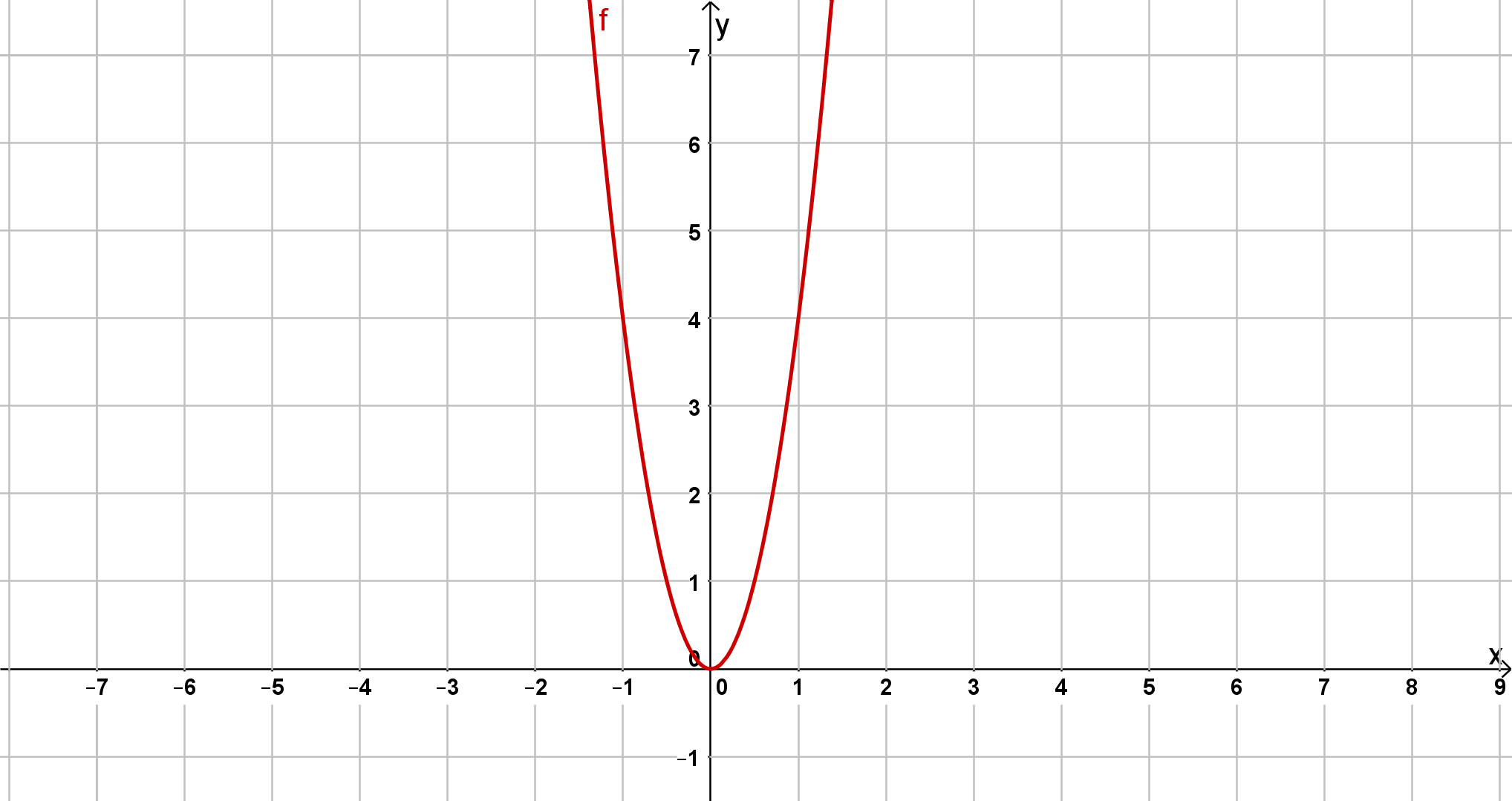
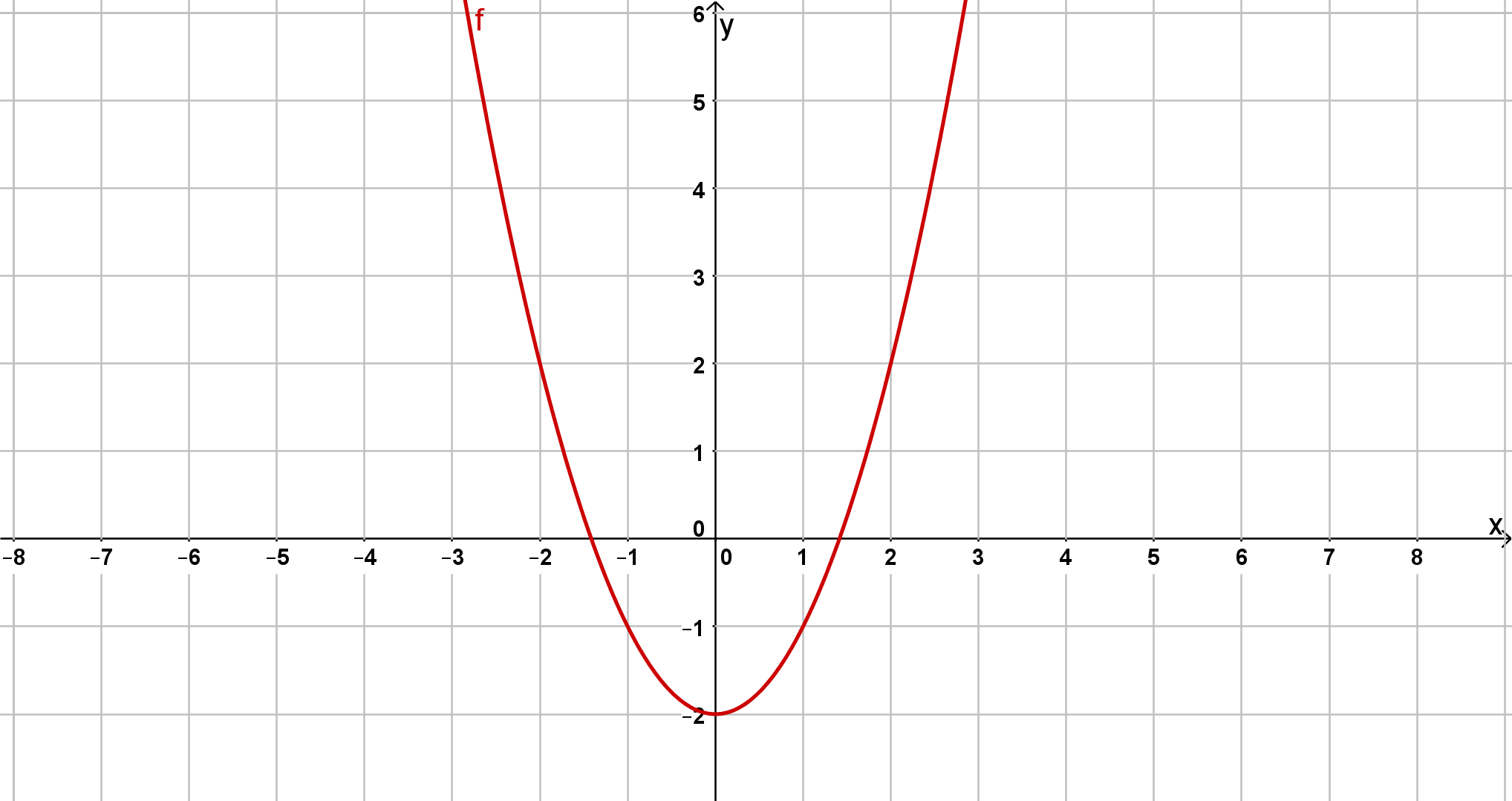
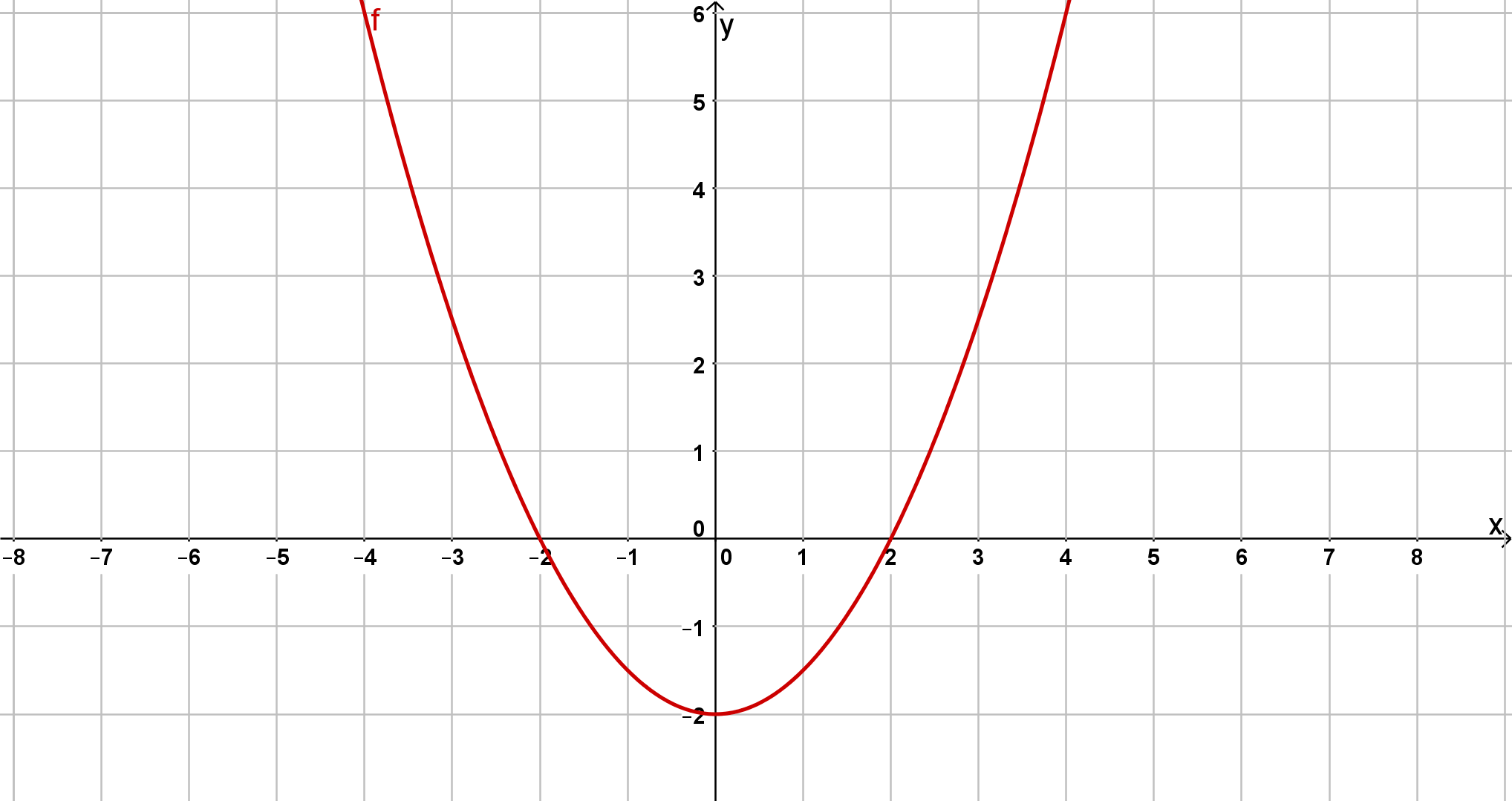
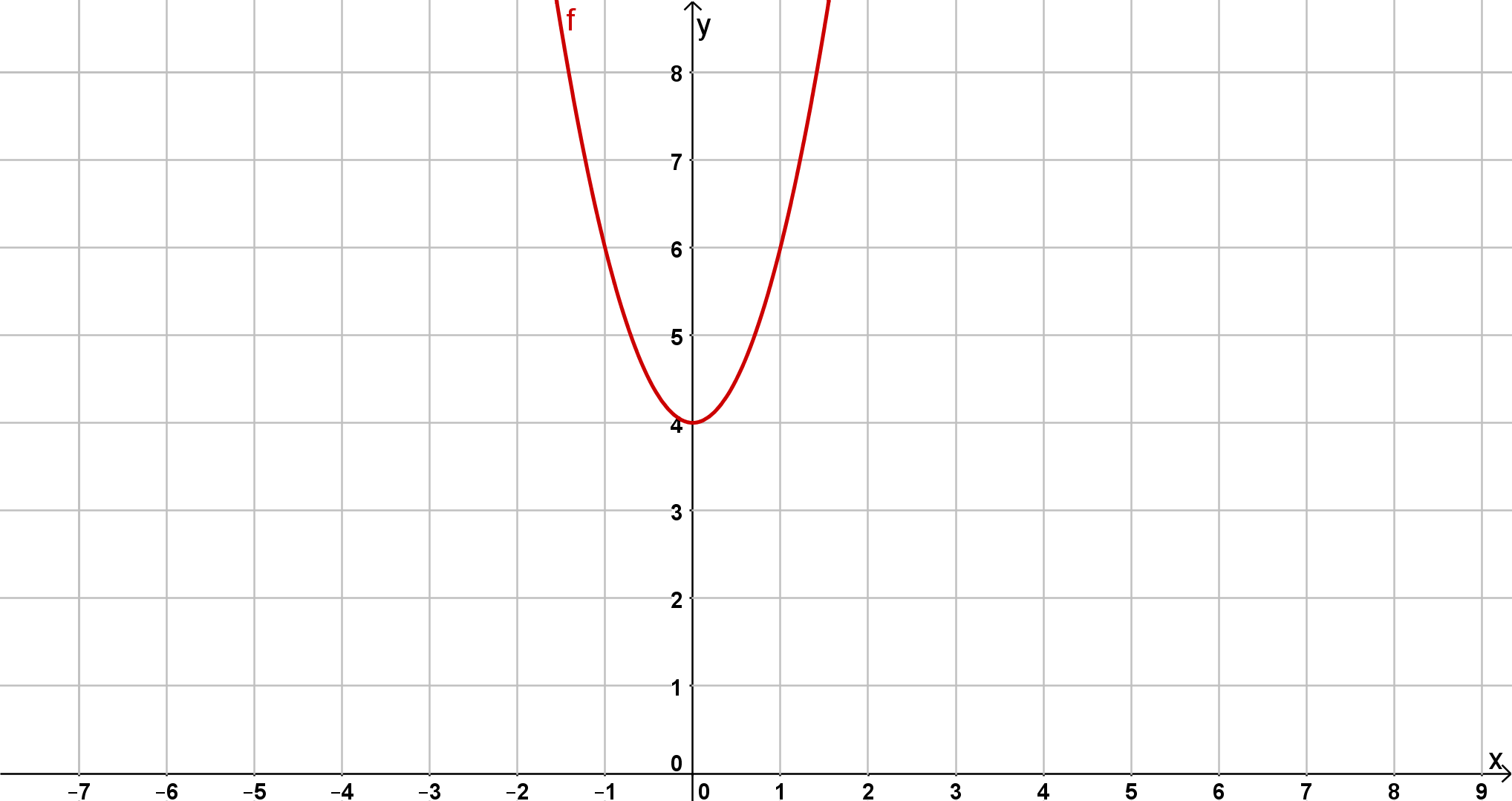
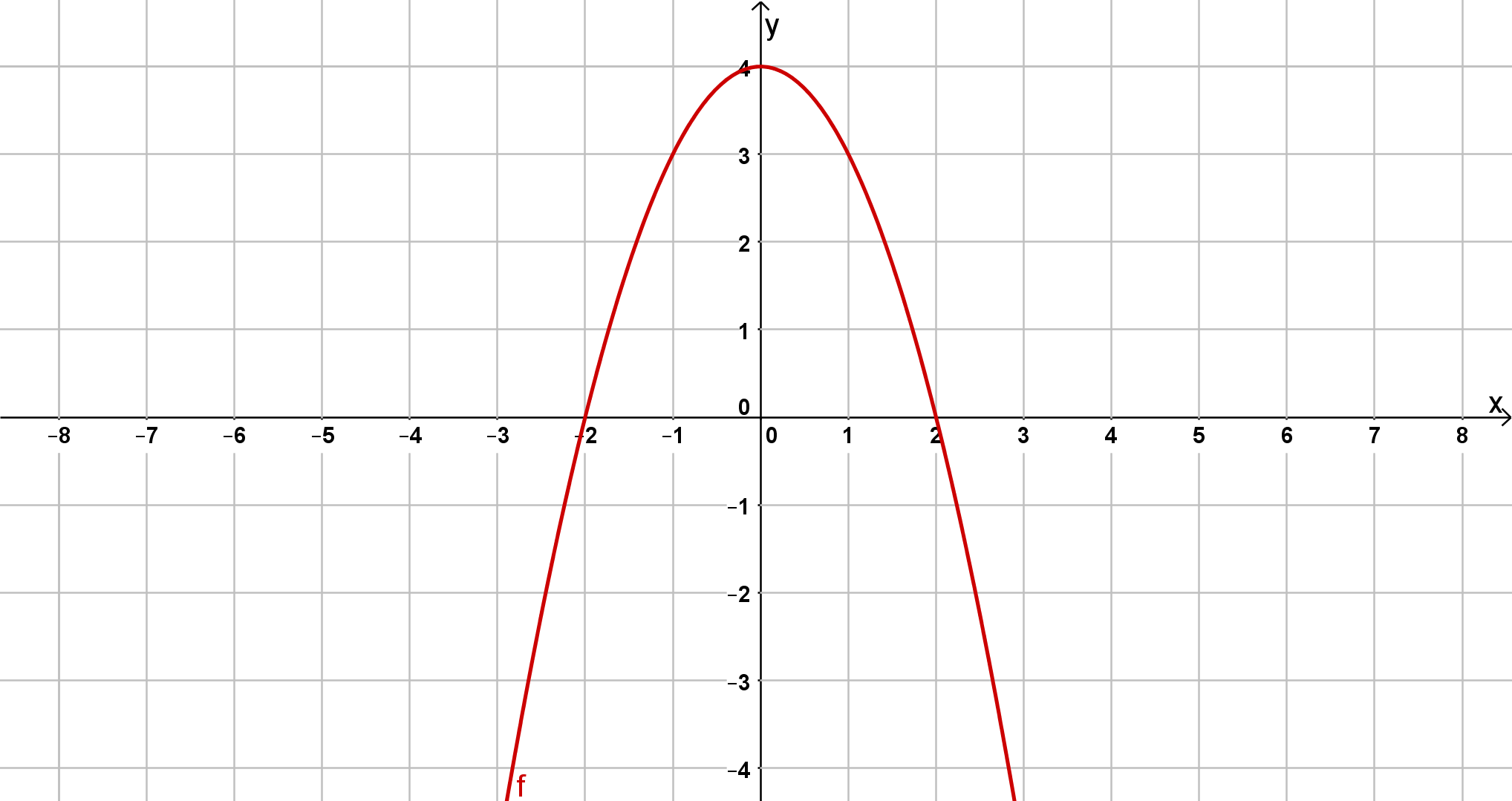
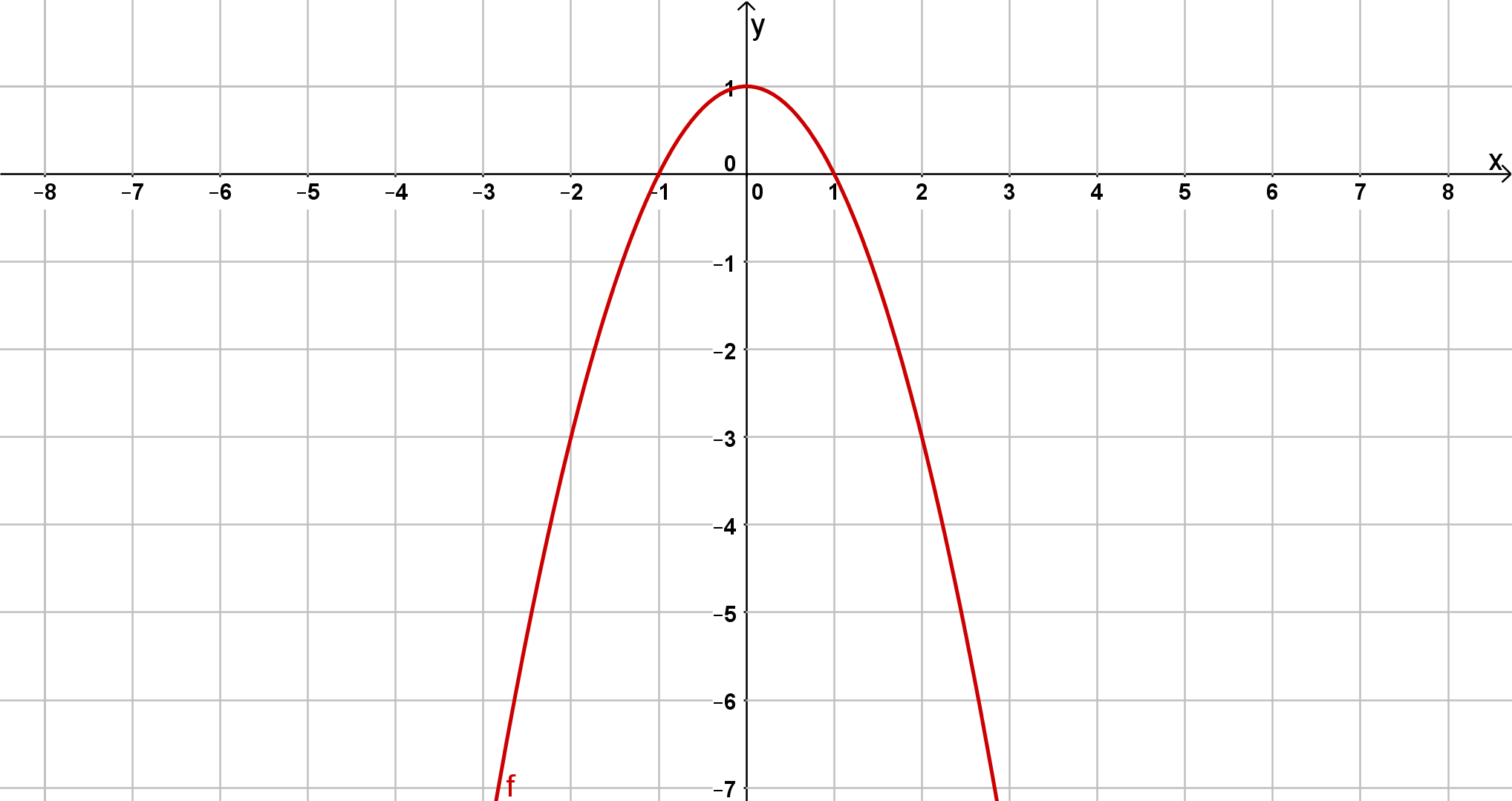
Bestimme jeweils die Scheitelform der unten abgebildeten Parabeln.
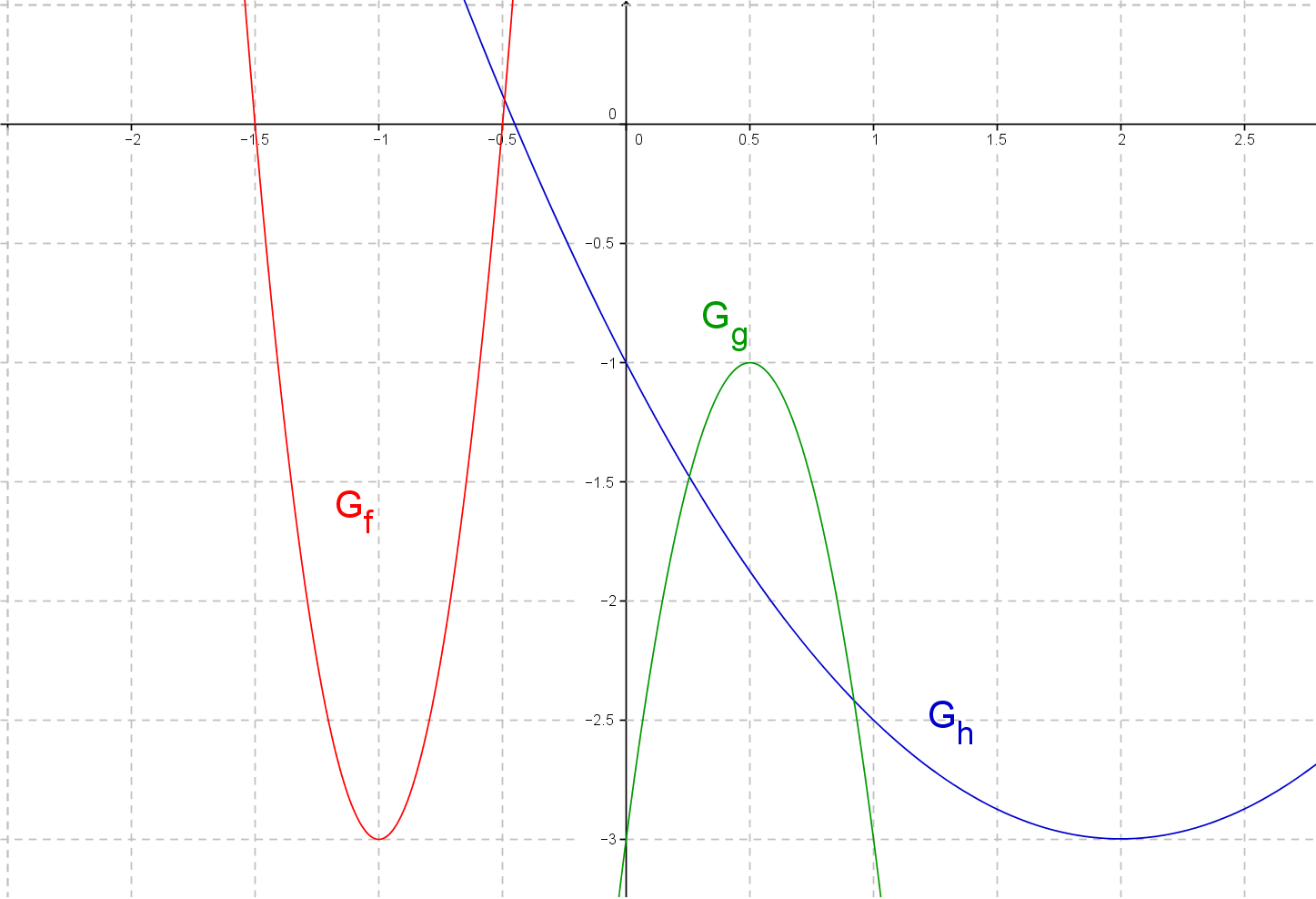
- 6
Zeichne die Graphen der folgenden Funktionen:
- 7
Bestimme den Öffnungsfaktor und den Funktionsterm der folgenden Parabeln!
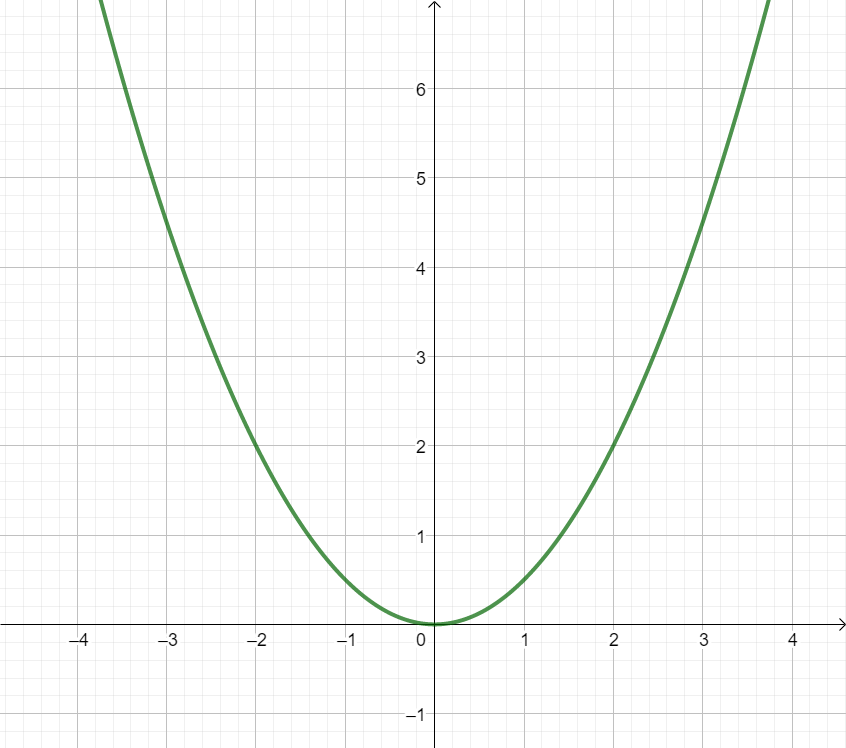
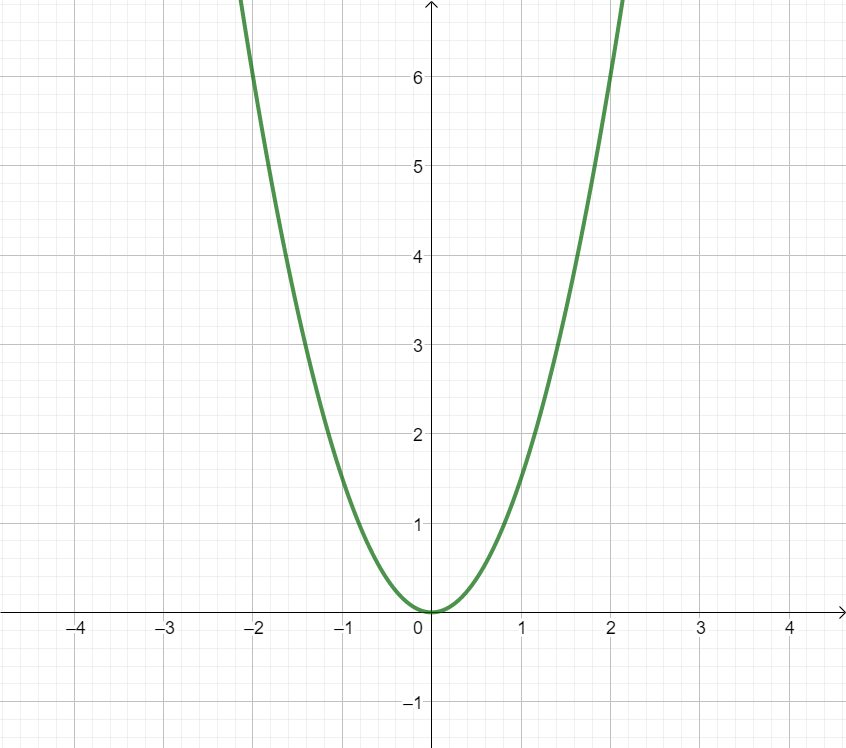
Bestimme den Funktionsterm einer Parabel mit dem Scheitelpunkt , die durch den Punkt geht.