Geometrie, Teil A, Aufgabengruppe 2

Teilaufgabe a)

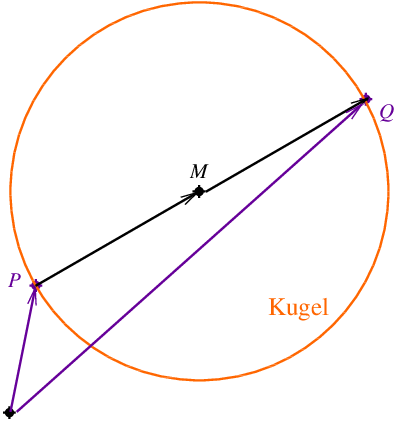
Zur Lösung der Aufgabe genügt es eine Vorstellung von der Lage der 3 Punkte $P$, $M$ und $Q$ zu haben. Vielleicht machst Du Dir dazu eine Planfigur, ähnlich der nachfolgenden Abbildung:

Zum Punkt $Q$ zeigt der Ortsvektor $\overrightarrow{q}=\overrightarrow{p}+2\cdot \overrightarrow{PM}$:

$\begin{array}{cl}\overrightarrow{q}& =\overrightarrow{p}+2\cdot \overrightarrow{PM}\\ & =\left(\begin{array}{c}3\\ 4\\ 4\end{array}\right)+2\cdot \left(\begin{array}{c}-3-3\\ 2-4\\ 7-4\end{array}\right)\\ & =\left(\begin{array}{c}3\\ 4\\ 4\end{array}\right)+2\cdot \left(\begin{array}{c}-6\\ -2\\ 3\end{array}\right)\\ & =\left(\begin{array}{c}-9\\ 0\\ 10\end{array}\right)\end{array}$

Das Vorgehen ist übrigens genauso, wie bei der Bestimmung des Spiegelpunkts bei Spiegelung an einem gegebenen Punkt.

Teilaufgabe b)

Zur Lösung dieser Aufgabe ist ein Verständnis der besonderen Ebenen, hier der Koordinaten-Ebenen, erforderlich und natürlich das Vorstellungsvermögen von der gegenseitigen Lage der typischen Objekte im Dreidimensionalen.

$x_1-x_2$-Koordinatenebene

Das kennzeichnende dieser Koordinatenebene ist, dass ihre $x_3$-Koordinate 0 ist, der Rest ist unbestimmt ("egal"). Genauso schreibt man es hin: $x_3=0$.

Abstand von der $x_1-x_2$-Koordinatenebene

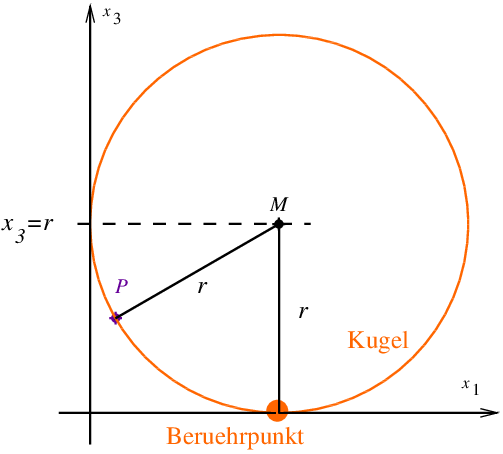
Wenn die Kugel die $x_1-x_2$-Ebene gerade berührt, dann muss der Mittelpunkt der Kugel gerade in der Entfernung des Kugelradius von der $x_1-x_2$-Ebene sein. Die $x_3$-Koordinate des Mittelpunkts $M$ beträgt $7$. Der Mittelpunkt ist also $7$ Längeneinheiten von der $x_1-x_2$-Ebene entfernt.

Die nachfolgende Skizze zeigt, wie man sich den Zusammenhang mit einer einfachen Planfigur klar machen kann:

Bleibt noch zu zeigen, dass der Kugelradius auch gerade den Wert $7$ hat:

Bestimmung des Kugelradius

Hierzu wird der Abstand des Punktes $P$ vom Kugelmittelpunkt $M$ berechnet:

$\begin{array}{cl}r& =d(P,M)\\ & =\left|\left(\begin{array}{c}-6\\ -2\\ 3\end{array}\right)\right|\\ & =\sqrt{(-6{)}^2+(-2{)}^2}+3^2\\ & =\sqrt{49}=7\end{array}$

Der Radius der Kugel ist also genauso groß wie die $x_3$-Koordinate ihres Mittelpunkts. Damit ist die Behauptung bewiesen.