Aufgaben zu Primzahlen

Beispiel

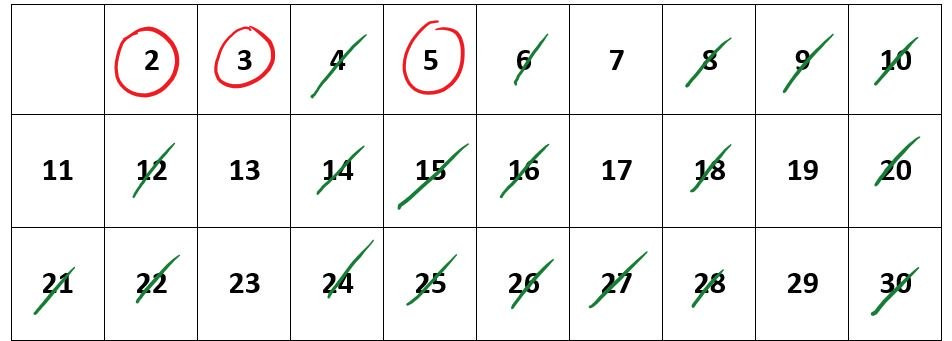
Mache dir den Zusammenhang zuerst an einem Beispiel klar. Betrachte dafür das Sieb des Eratosthenes für die Zahlen $\{2,\dots ,30\}$.

In dieser Tabelle wurden die Verfahrensschritte für die Primzahlen $2,3$ und $5$ bereits durchgeführt. Nun ist $7>\sqrt{30}\approx \mathrm{5,48}$, das heißt alle Verfahrensschritte für Primzahlen $p<\sqrt{30}$ wurden durchgeführt. Weiter ist jedes Vielfache von $7,11,13,17,19,23$ und $29$ in der Liste bereits durchgestrichen.

Betrachte zum Beispiel die Zahl $14$. Diese ist ein Vielfaches von $7$, denn $14=2\cdot 7$. Aber sie wurde bereits durchgestrichen, als du die Vielfachen von $2$ durchgestrichen hast.

Somit kannst du alle weiteren Zahlen, die noch nicht durchgestrichen wurden, umkringeln, da diese Primzahlen sind.

Erklärung für allgemeines $n$

Wir nehmen an, dass wir die Verfahrensschritte für Primzahlen $p\le \sqrt{n}$ bereits durchgeführt haben. Dann ist jede Zahl $k$ mit $\sqrt{n}<k\le n$, die ein Vielfaches einer Primzahl $q$ mit $q>\sqrt{n}$ ist, bereits durchgestrichen. Die Verfahrensschritte brauchen also für Primzahlen $q$ mit $q>\sqrt{n}$ nicht durchgeführt werden.

Da $k$ ein Vielfaches von $q$ ist, lässt sich $k$ darstellen als $k=q\cdot r$ mit $r>1$. Damit ist aber $r\le \sqrt{n}$. Denn wäre $r>\sqrt{n}$, dann wäre $k=q\cdot r>\sqrt{n}\cdot \sqrt{n}=n$, im Widerspruch zur Voraussetzung, dass $k\le n$ ist. Die zusammengesetzte Zahl $k$ ist also als Vielfaches von $r$ mit $r\le \sqrt{n}$ bereits durchgestrichen.