Analysis, Teil A, Aufgabengruppe 2

Gegeben ist die Funktion $f$ mit $f (x) = \frac{(3 + x)^{2}}{x - 1}$ und maximalem Definitionsbereich $D$ . Der Graph von $f$ wird mit $G_{f}$ bezeichnet.

$a)$ Geben Sie $D$ und die Koordinaten der Schnittpunkte von $G_{f}$ mit den Koordinatenachsen an. (3 BE)

$b)$ Zeigen Sie, dass $f (x)$ zum Term $x + 7 + \frac{16}{x - 1}$ äquivalent ist, und geben Sie die Bedeutung der Geraden $g$ mit der Gleichung $y = x + 7$ für $G_{f}$ an. (3 BE)

Lösung zur Teilaufgabe a)

Bestimmung von $D$

Du musst den Definitonsbereich bestimmen. Dafür bestimmt man als Erstes den Funktionstyp. Es handelt sich hier um eine gebrochen-rationale Funktion, also musst du für die Definitionmenge die Definitionslücken, das heißt die Nullstellen des Nenners berechnen.

$x - 1 = 0 | + 1$

$x = 1$

Der Nenner hat seine Nullstelle bei $x = 1$ , also ist die Definitionsmenge $D = ℝ \ {1}$ .

Schnittpunkt mit der $y$ -Achse

Für die Bestimmung des Schnittpunktes mit der $y$ -Achse musst du $0$ in die Funktion einsetzen.

$f (0) = \frac{(3 + 0)^{2}}{0 - 1} = \frac{9}{- 1} = - 9$

Da nach dem Schnittpunkt gefragt ist, musst du das Ergebnis als Punkt angeben: $S_{y} (0 | - 9)$ .

Schnittpunkt mit der x-Achse

Für die Berechnung des Schnittpunktes mit der x-Achse musst du die Funktion mit $0$ gleichsetzen.

$\frac{(3 + x)^{2}}{x - 1} = 0$

Eine gebrochen-rationale Funktion ist genau dann 0, wenn der Zähler 0 ist.

$\begin{array}{rrl} (3 + x)^{2} & = & 0 & | \sqrt{()} \\ 3 + x & = & 0 & | - 3 \\ x & = & - 3 \end{array}$

Auch hier musst du die Lösung noch in Punktschreibweise angeben: $S_{x} (- 3 | 0)$ .

Lösung zur Teilaufgabe b)

Äquivalenz der Terme

Um zu zeigen, dass zwei Terme äquivalent sind, musst du dir überlegen, wie du durch gleichwertige Umformungen aus dem ersten Term den zweiten erhalten kannst.

Als Erstes bietet es sich an, die Klammer im Zähler von $f (x)$ aus zu multiplizieren. Denke dabei an die binomische Formel!

$f (x) = \frac{(3 + x)^{2}}{x - 1} = \frac{9 + 6 x + x^{2}}{x - 1}$

Jetzt hast du zwei Möglichkeiten: Entweder du führst für $f (x)$ eine Polynomdivision durch oder du erweiterst den Summenterm, sodass dieser nur noch ein Bruch ist. Hier wird die zweite Version vorgestellt.

$x + 7 + \frac{16}{x - 1} = \frac{(x + 7) (x - 1)}{x - 1} + \frac{16}{x - 1} = \frac{(x + 7) (x - 1) + 16}{x - 1} = \frac{x^{2} - x + 7 x - 7 + 16}{x - 1} = \frac{x^{2} + 6 x + 9}{x - 1} = f (x)$

Der Term kann also umgeformt werden, dass am Schluss eine Version von $f (x)$ dasteht.

Bedeutung von $x + 7$

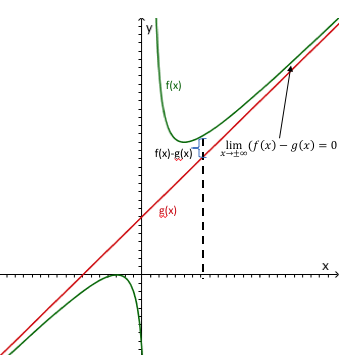
Bei der Geraden $g$ mit $y = x + 7$ handelt es sich um die schräge Asymptote des Graphen von $f (x)$ . Falls dir nicht klar ist, wieso das so ist, lies dir am besten den Artikel zu Asymptoten durch.