Aufgaben zu Steigung und Differenzierbarkeit anhand des Graphen
Graphisches Differenzieren einer linearen Funktion
Die lineare Funktion soll graphisch differenziert werden.
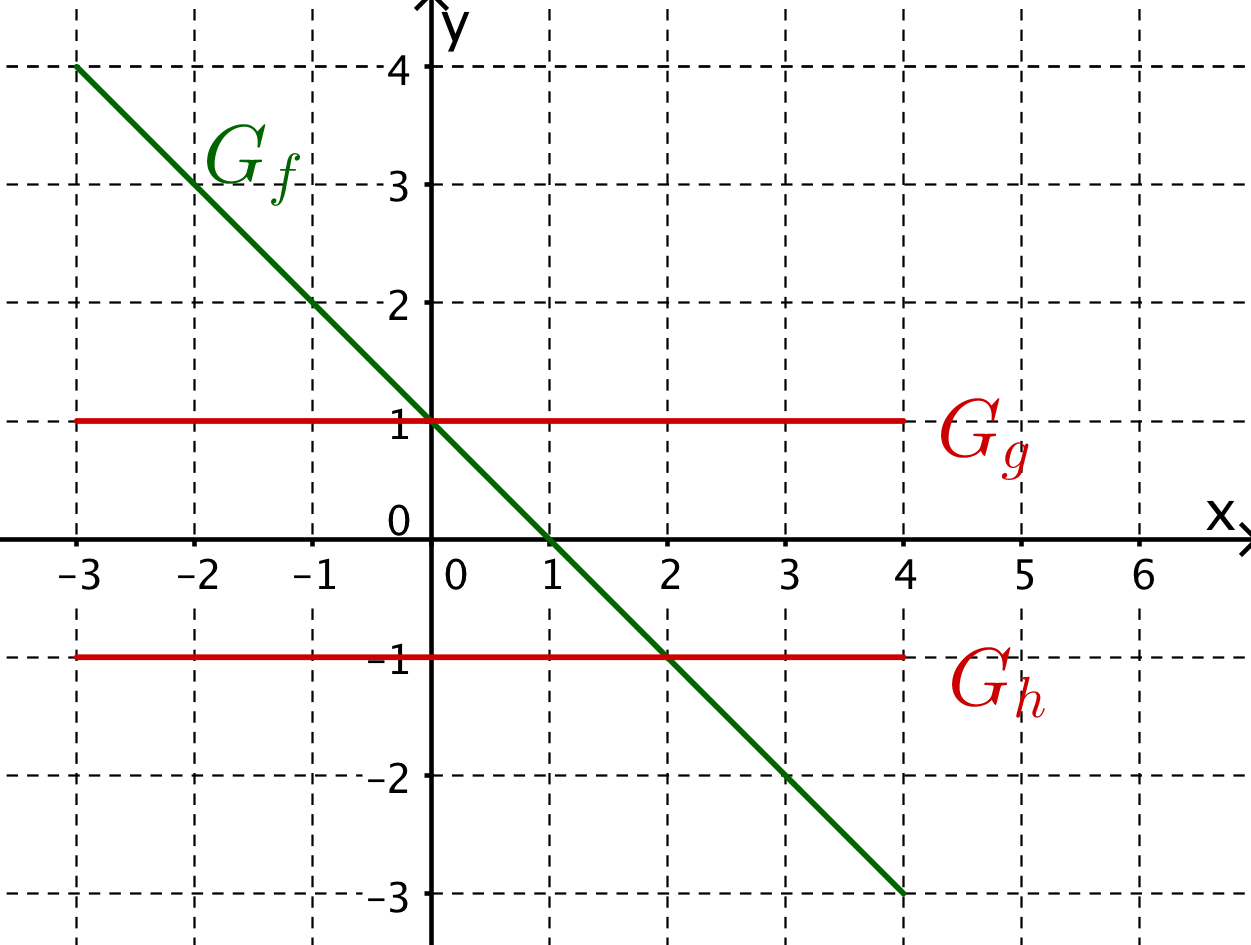
Betrachte die gegebenen Graphen und entscheide, was zutrifft.
Graphisches Differenzieren einer ganzrationalen Funktion 2. Grades
Die quadratische Funktion p soll graphisch differenziert werden.
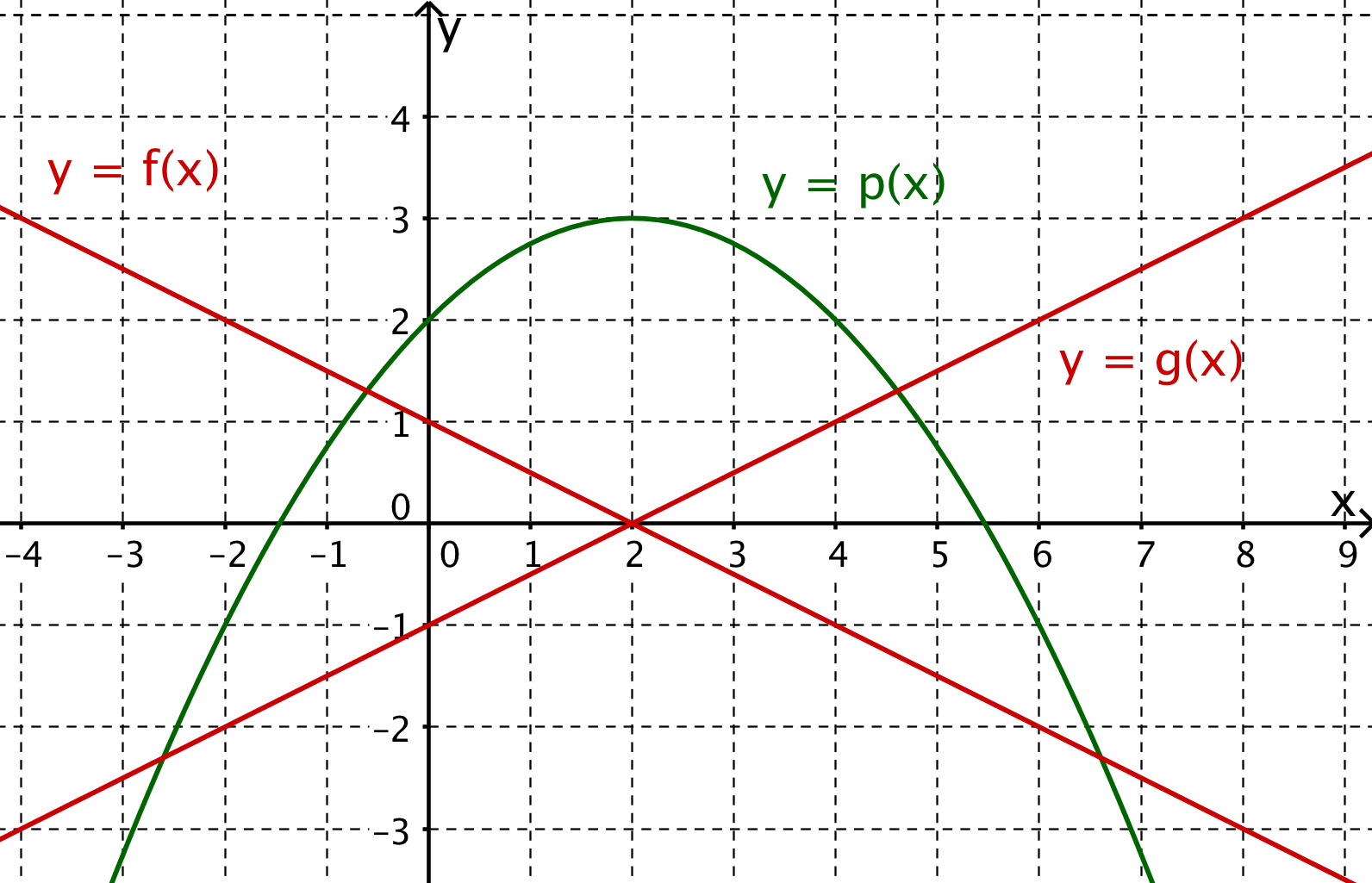
Entscheide, welche der beiden Funktionen oder die Ableitungsfunktion von p ist.
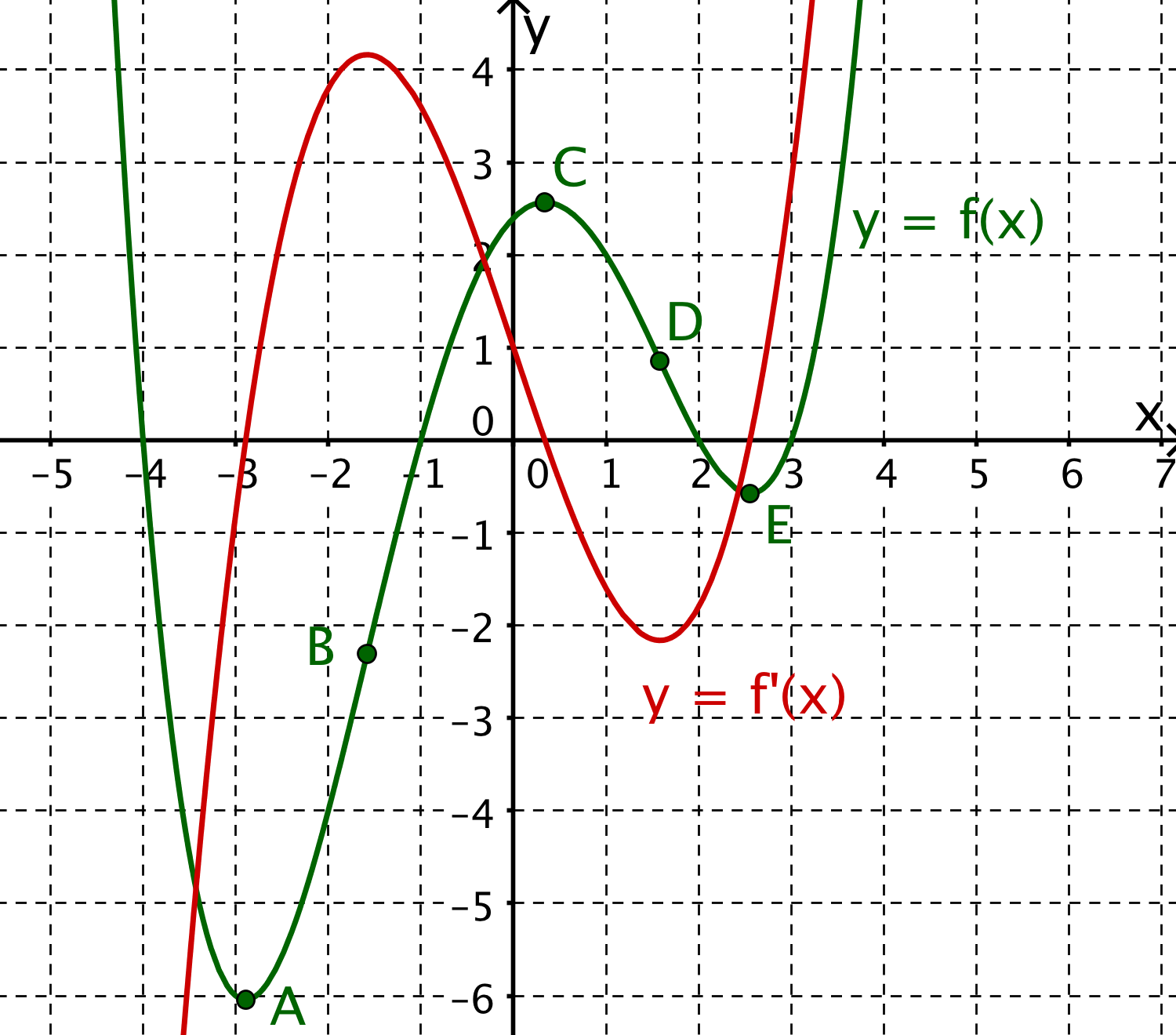
Graphisches Differenzieren einer ganzrationalen Funktion höheren Grades
Fertige durch graphisches Differenzieren eine Skizze der Ableitungsfunktion der nachfolgenden ganzrationalen Funktion 4. Grades.
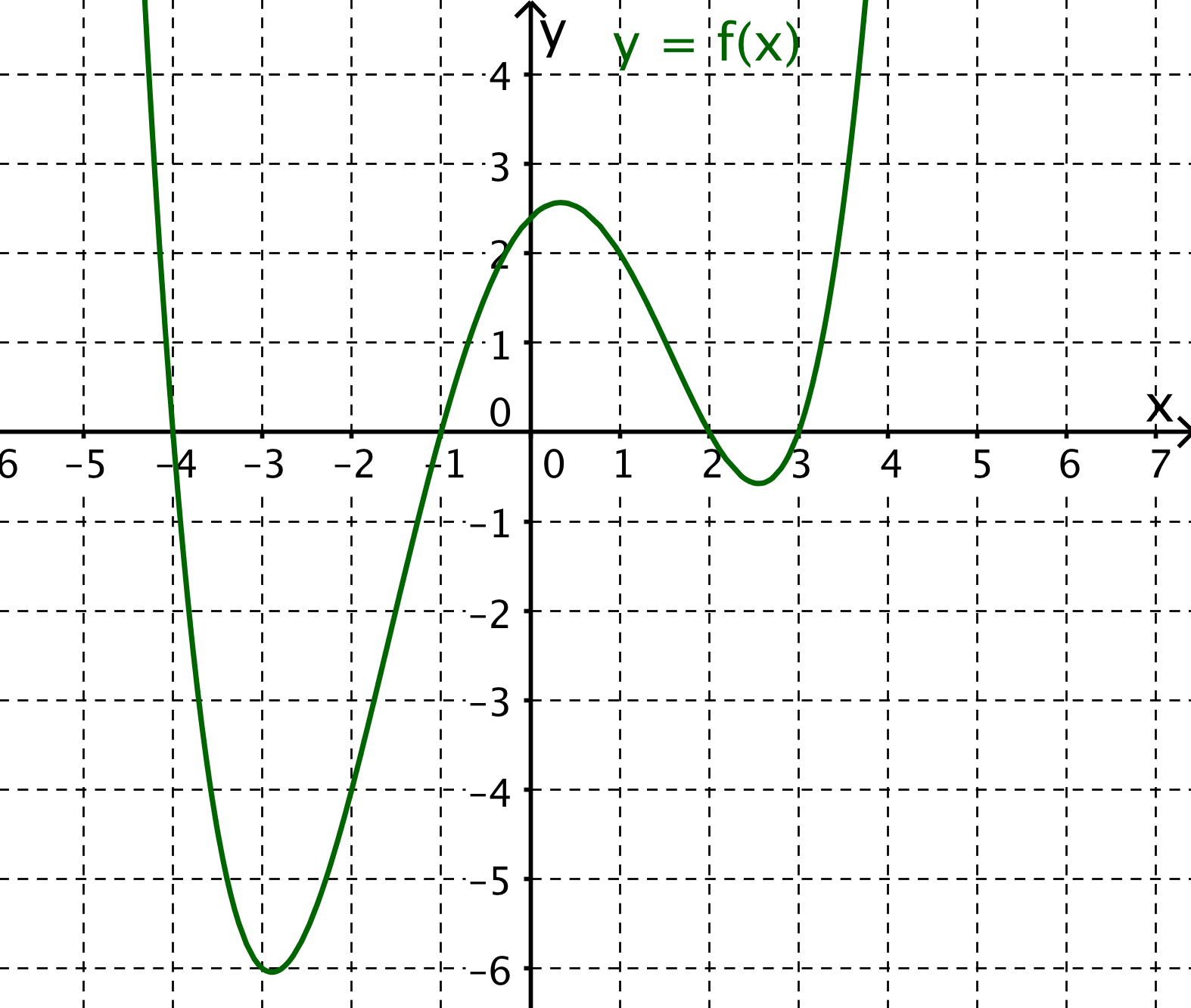
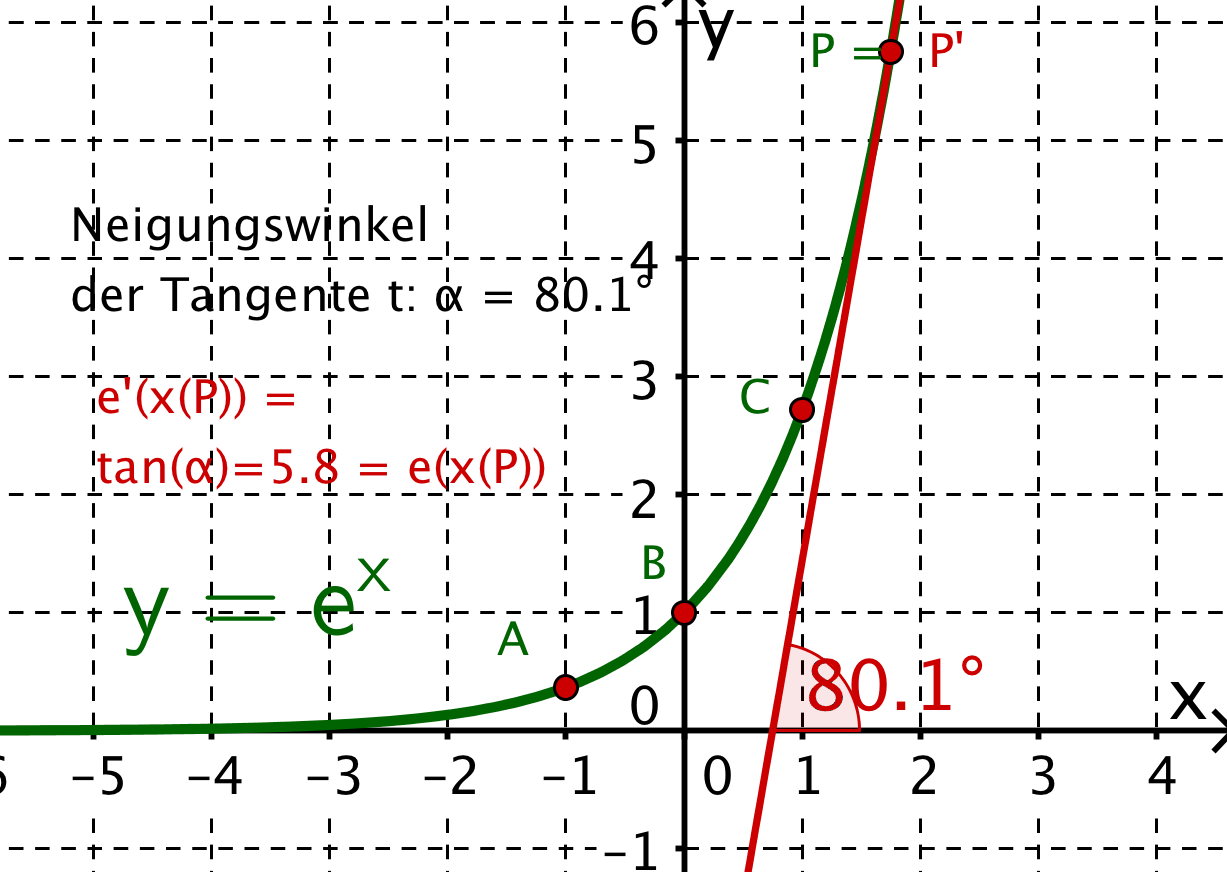
Graphisches Differenzieren der e-Funktion
Die e-Funktion ist für viele Anwendungsgebiete der Mathematik eine der wichtigsten Funktionen.
Graphisch gesehen ist sie aber eher eine besonders "langweilige" Funktion: ohne Nullstellen, ohne lokale Extrema und ohne Wendepunkte - einfach nur steigend.
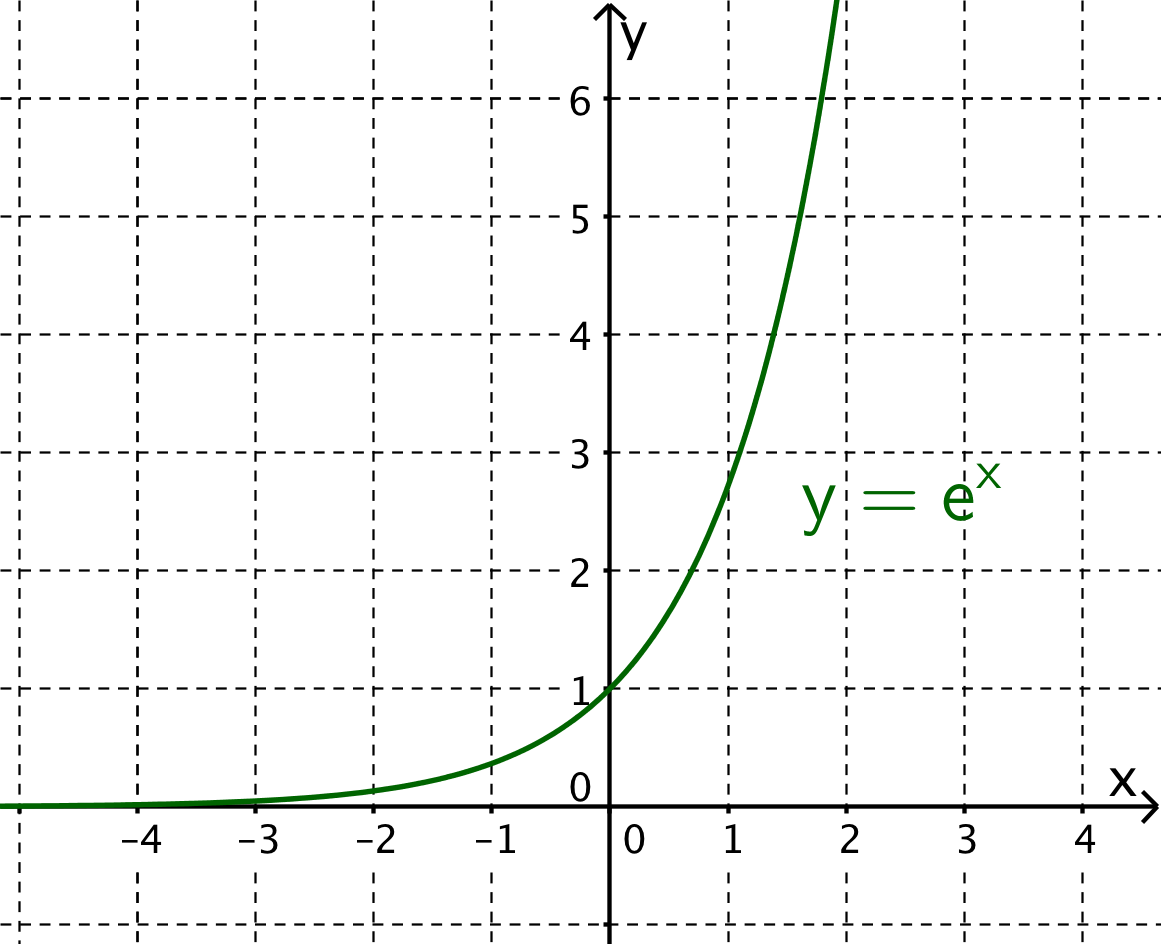
Welche überraschende Besonderheit der e-Funktion entdeckst du aber, wenn du dich um eine möglichst genaue Skizze beim graphischen Differenzieren der e-Funktion bemühst?
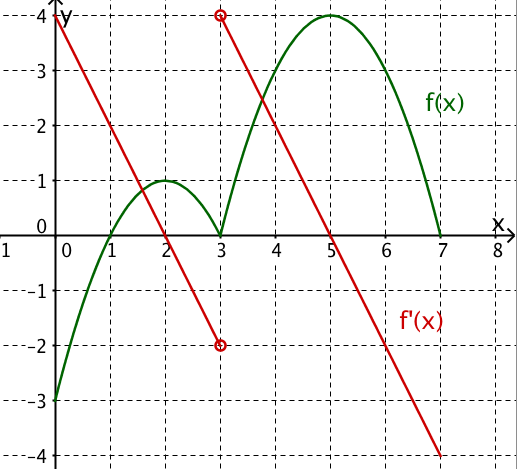
Graphisches Differenzieren einer abschnittsweise definierten Funktion
Die folgende Funktion ist graphisch zu differenzieren.
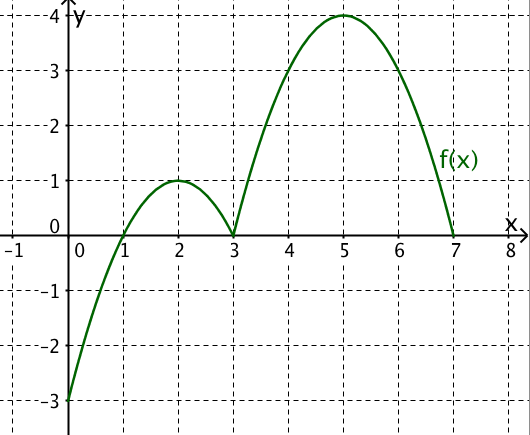
Klicke die richtige Lösung an!