Gemischte Aufgaben zum Bruchverständnis
Gib den gefärbten Anteil als Bruch an.
Schreibweise: Trenne Zähler und Nenner mit einem "/".
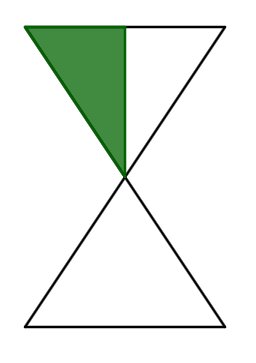
Tipp: Überlege dir, wie du die Sanduhr in gleich große Flächen unterteilen kannst.
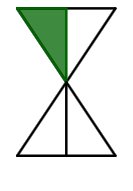
Die Sanduhr kannst du in vier gleich große Dreicke teilen. Die Teile sind also Viertel.
Von den Vierteln ist 1 Viertel farbig. Der Zähler ist also 1.
Lösung:
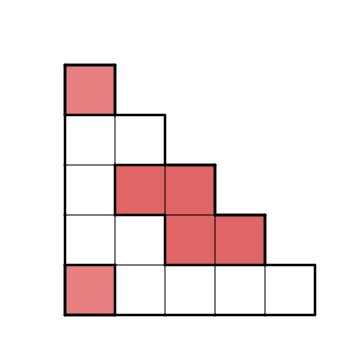
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche darstellen
Die Figur besteht aus Quadraten, der Nenner ist also .
Von den 15 Quadraten sind farbig. Der Zähler ist also .
Lösung:
Falls du schon kürzen kannst: ist auch richtig.
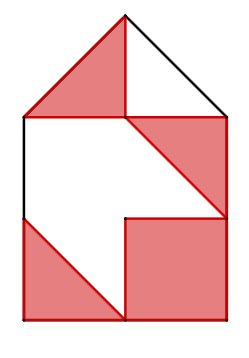
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche
Gesucht: Bruchteil der farbigen Felder
Teile die Figur so, dass kongruente Dreiecke entstehen, siehe Skizze.
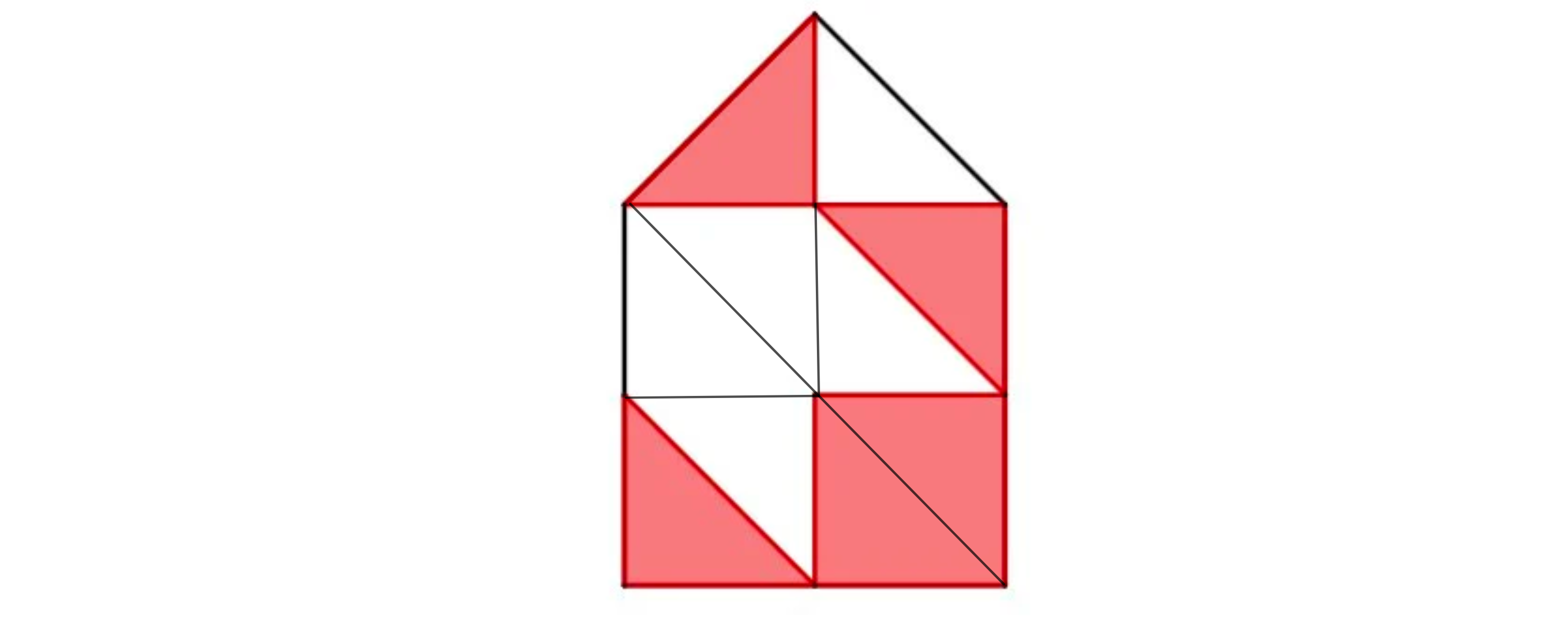
Die Figur besteht aus Dreiecken, der Nenner ist also 10.
Von den Dreiecken sind farbig. Der Zähler ist also .
Lösung:
Falls du schon kürzen kannst: ist auch richtig.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche
Gesucht:
Bruchteil der farbigen Felder:
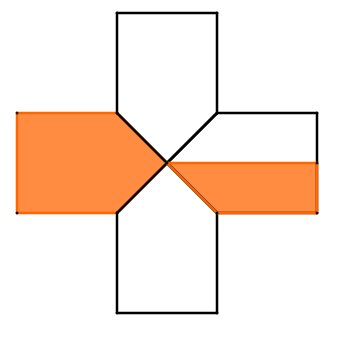
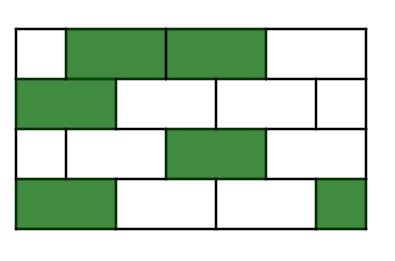
Teile die Figur so, dass deckungsgleiche Trapeze entstehen, siehe Skizze.
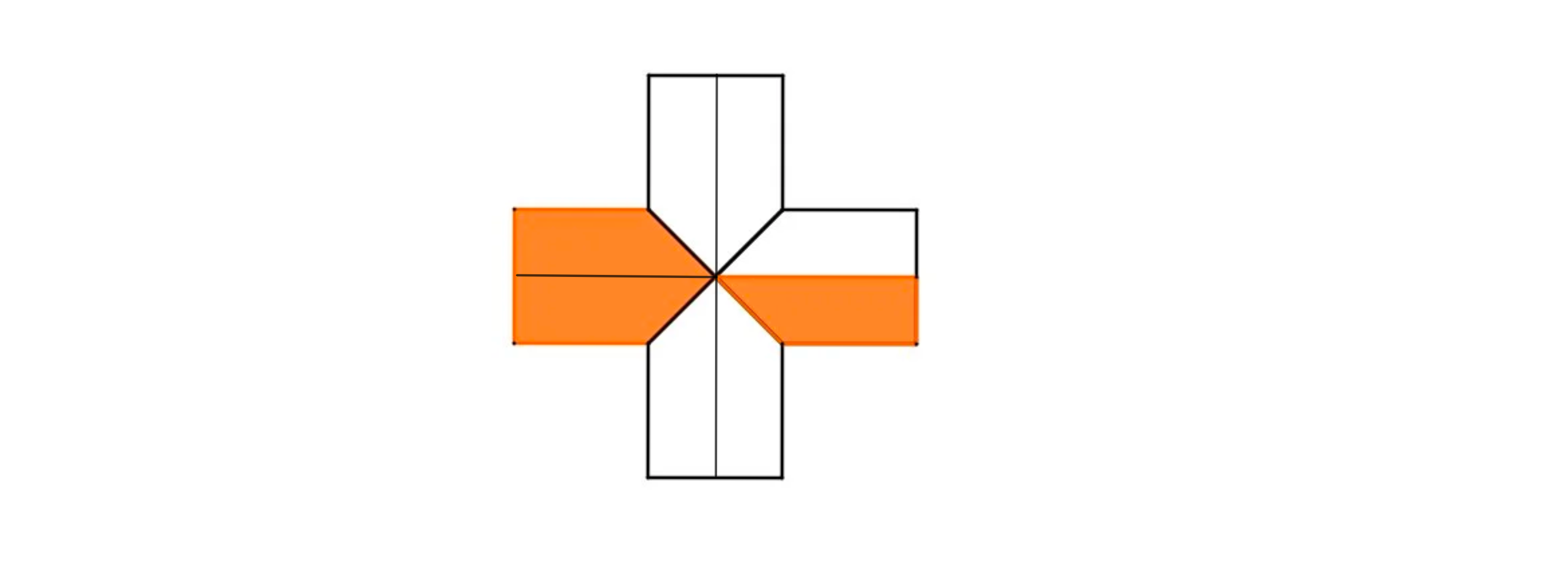
Die Figur besteht aus Trapezen, der Nenner ist also .
Von den Trapezen sind farbig. Der Zähler ist also .
Lösung:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche
Gesucht:
Bruchteil der farbigen Felder
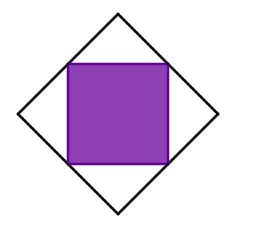
Teile die Figur so, dass kongruente Dreiecke entstehen, siehe Skizze.
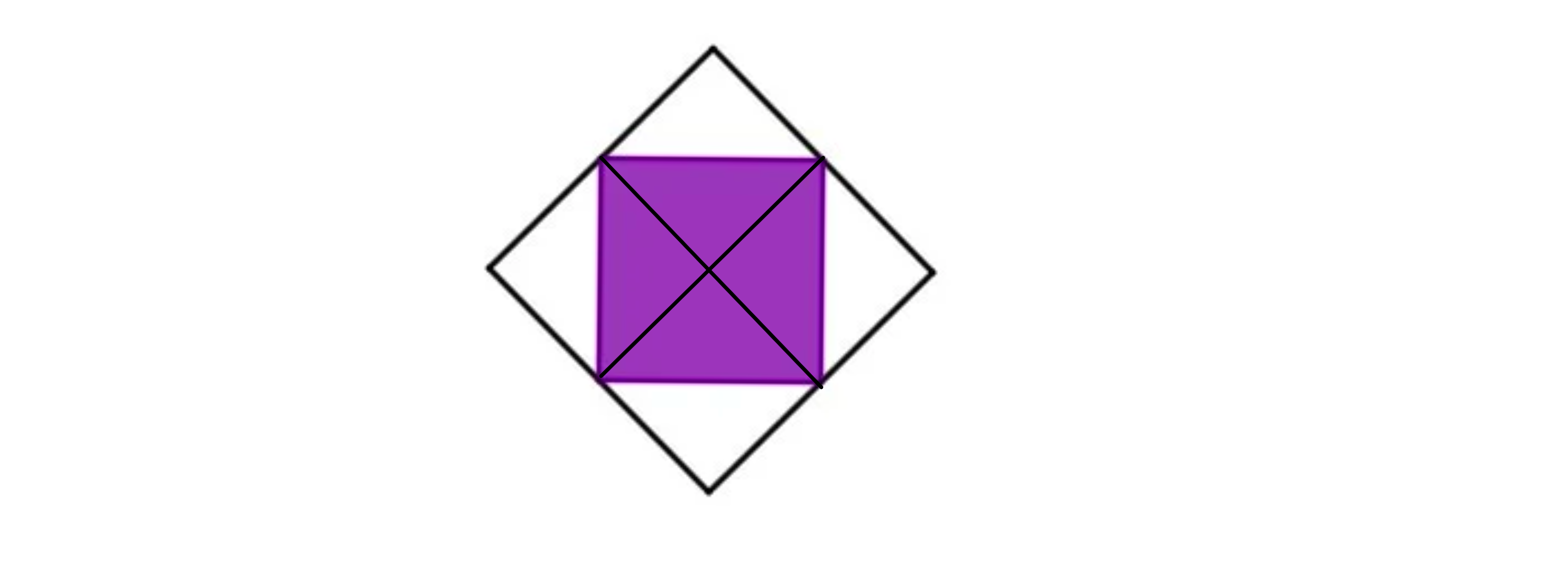
Die Figur besteht aus Dreiecken, der Nenner ist also .
Von den Dreiecken sind farbig. Der Zähler ist also .
Lösung:
Falls du schon kürzen kannst: ist auch richtig.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche
Gesucht:
Bruchteil der farbigen Felder
Teile die Figur so, dass gleich grosse Felder entstehen, siehe Skizze.
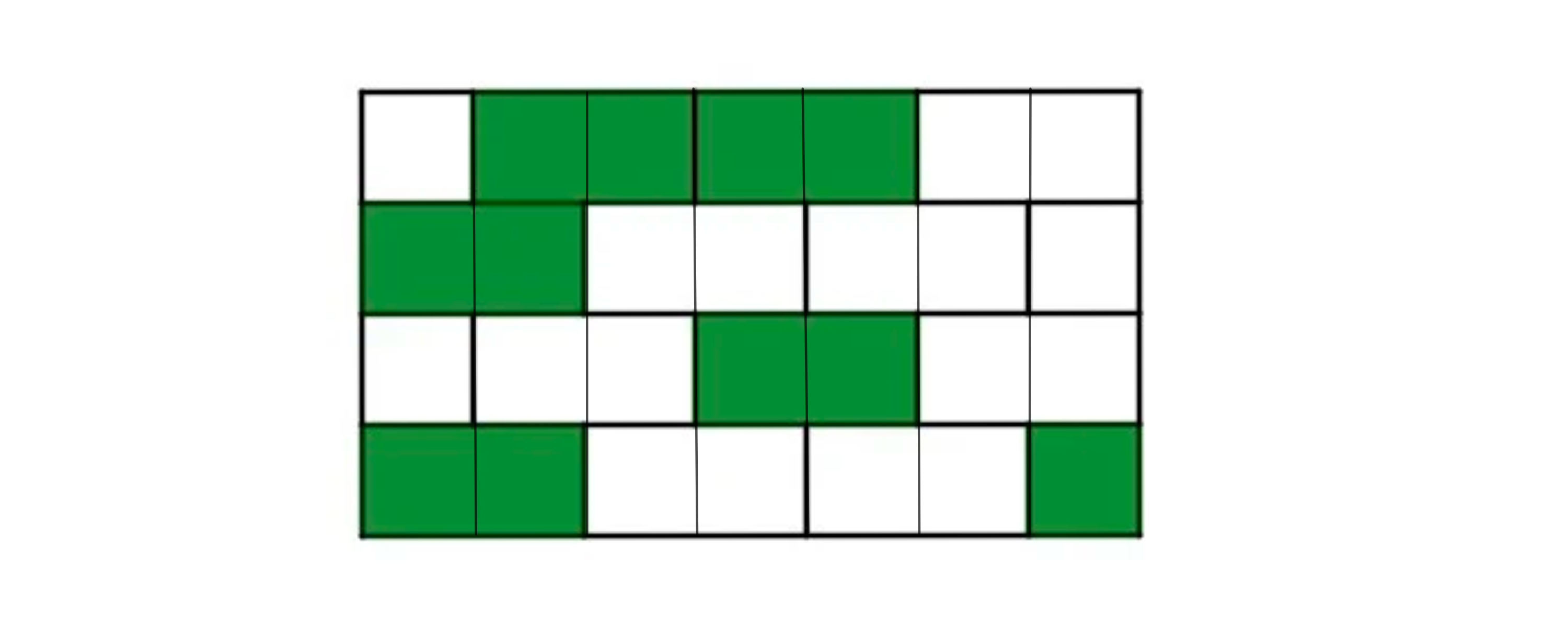
Die Figur besteht aus Quadraten, der Nenner ist also .
Von den 28 Quadraten sind farbig. Der Zähler ist also .
Lösung:


