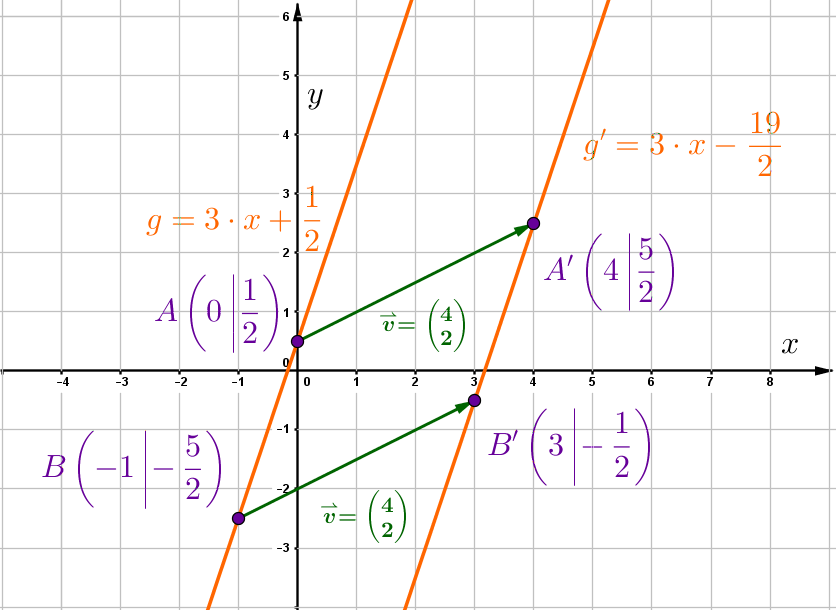
Aufgaben zur Parallelverschiebung
Verschiebe die Gerade um den Vektor .
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallelverschiebung einer Gerade
↓ Setze die Geradengleichung in die Matrixform ein.
↓ Damit erhältst du zwei Gleichungen in Abhängigkeit von .
Löse die erste Gleichung nach x auf und setze sie in die zweite Gleichung ein:
Somit hast du die neue Geradengleichung in Abhängigkeit von .
Alternativlösung
Wähle zwei Punkte, die auf der Gerade liegen, z.B. den x- und y-Achsenabschnitt.
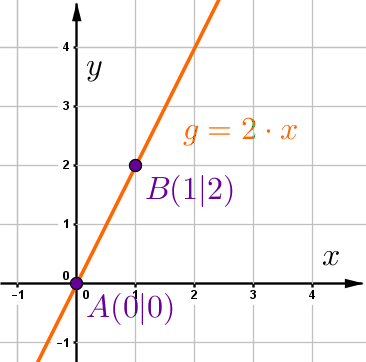
und
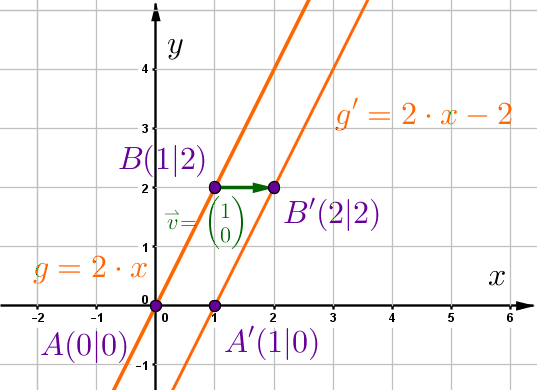
Verschiebe die Punkte und um den Vektor .
1. Variante: Berechnung in Koordinatenform
Addiere den Vektor zu den Ortsvektoren und
Setze die Koordinaten der Punkte ein.
2. Variante: Berechnung in Matrixform
↓ Führe die Matrix-Vektor-Multiplikation durch.
↓ ↓ Führe die Matrix-Vektor-Multiplikation durch.
↓ und
Berechne die Steigung durch den Differenzenquotienten.
Setze und den Punkt in die Geradengleichung ein und stelle sie um, um zu bestimmen.
Stelle die Geradengleichung auf.
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallelverschiebung einer Gerade
,
↓ Setze die Geradengleichung in die Matrixform ein.
↓ Damit erhältst du zwei Gleichungen in Abhängigkeit von x.
Löse die erste Gleichung nach x auf und setze sie in die zweite Gleichung ein.
Somit hast du die neue Geradengleichung in Abhängigkeit von
Alternativlösung:
Wähle zwei Punkte, die auf der Gerade liegen, z.B. den x- und y-Achsenabschnitt. In diesem Fall betrachtest du den y-Abschnitt und gehst dann nach unten und nach links, sodass du bei landest.
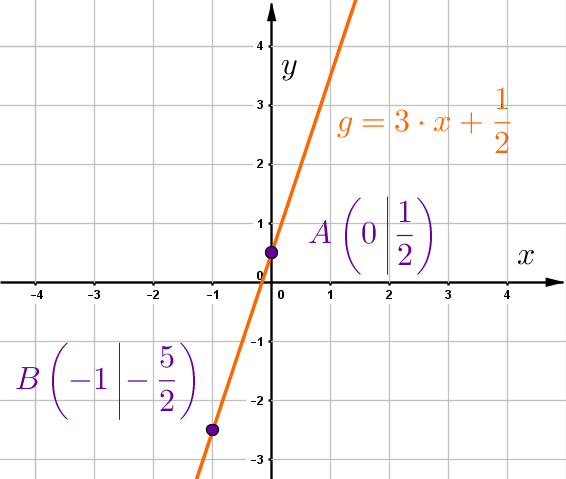
und
Verschiebe die Punkte und um den Vektor
1. Variante: Berechnung in Koordinatenform
Addiere den Vektor zu den Ortsvektoren und
Setze die Koordinaten der Punkte ein.
2. Variante: Berechnung in Matrixform
↓ Führe die Matrix-Vektor-Multiplikation durch.
↓ ↓ Führe die Matrix-Vektor-Multiplikation durch.
↓ und
Berechne die Steigung durch den Differenzenquotienten.
Setze und den Punkt in die Geradengleichung ein und stelle sie um, um zu bestimmen.
Stelle die Geradengleichung auf.