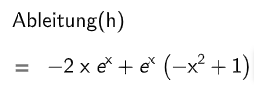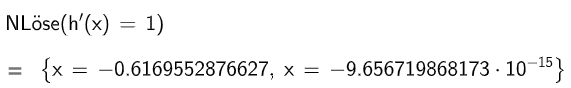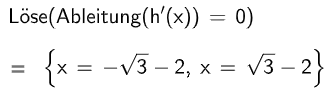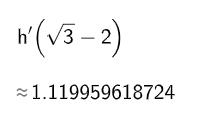Teil B: Analysis 1

Aufgabe 2

Gegeben ist die in $ℝ$ definierte Funktion $h$ mit $h (x) = (1 - x^{2}) \cdot e^{x}$ . Der Graph von $h$ wird mit $G_{h}$ bezeichnet.

Begründen Sie anhand des Funktionsterms, dass der Funktionswert $h (x)$ nur für $- 1 < x < 1$ positiv ist. (3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: e-Funktion
Begründe anhand des Funktionsterms, dass der Funktionswert $h (x)$ nur für $- 1 < x < 1$ positiv ist
Gegeben ist $h (x) = (1 - x^{2}) \cdot e^{x}$ .
Es gilt: Für alle $x \in ℝ$ ist $e^{x} > 0$ .
$h (x)$ ist also genau dann positiv, wenn $(1 - x^{2}) > 0$ ist, also nur für $- 1 < x < 1$ .
Betrachte den Term $1 - x^{2}$ .
Für welche Werte von $x$ ist dieser Term positiv?
Die Gerade $u$ ist die Tangente an $G_{h}$ im Punkt $P (0 | 1)$ .
Es gibt einen weiteren Punkt $Q$ auf $G_{h}$ , in dem die Tangente $v$ an $G_{h}$ zu $u$ parallel ist.
Bestimmen Sie die x-Koordinate von $Q$ gerundet auf zwei Nachkommastellen. (4 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
Bestimme die x-Koordinate von $Q$ gerundet auf zwei Nachkommastellen
Bekannt ist: "Die Gerade $u$ ist die Tangente an $G_{h}$ im Punkt $P (0 | 1)$ .
Es gibt einen weiteren Punkt $Q$ auf $G_{h}$ , in dem die Tangente $v$ an $G_{h}$ zu $u$ parallel ist."
Berechne $h^{'} (x)$ :
$h^{'} (x) = e^{x} (- x^{2} - 2 x + 1)$
Im Punkt $P (0 | 1)$ ist $h^{'} (0) = 1 \Rightarrow$ die Gerade $u$ hat die Steigung $m_{u} = 1$ .
Für die parallele Tangente $v$ muss $m_{v} = m_{u}$ gelten.
Löse die Gleichung $h^{'} (x) = 1$ :
Die einzige weitere Lösung der Gleichung $h^{'} (x) = 1$ und damit die gesuchte Koordinate hat gerundet auf zwei Nachkommastellen den Wert $- 0,62$ .
Berechne $h^{'} (0)$ . Die Gerade $u$ hat die Steigung $m_{u} = h^{'} (0)$ .
Für die parallele Tangente $v$ muss $m_{v} = m_{u}$ gelten.
Löse die Gleichung $h^{'} (x) = h^{'} (0)$ .
Berechnen Sie die Wendestellen von $h$ , ohne dabei an Funktionsgraphen abgelesene Werte oder Zusammenhänge zu verwenden.
In einem der Wendepunkte von $G_{h}$ ist die Steigung von $G_{h}$ maximal.
Berechnen Sie den Wert der maximalen Steigung. (4 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wendepunkte und Terrassenpunkte
Berechne die Wendestellen von $h$ , ohne dabei an Funktionsgraphen abgelesene Werte oder Zusammenhänge zu verwenden
Löse die Gleichung $h^{''} (x) = 0$ .
Die Lösungen der Gleichung $h^{''} (x) = 0$ sind $x_{1} = - \sqrt{3} - 2 \approx - 3,73$ und $x_{2} = \sqrt{3} - 2 \approx - 0,27$ .
Wenn $h^{''} (x_{0}) = 0$ ist und zusätzlich $h^{'''} (x_{0}) \neq 0$ gilt, dann besitzt $h$ an der Stelle $x_{0}$ einen Wendepunkt.
Berechne $h^{'''} (x_{1})$ und $h^{'''} (x_{2})$ :
Da $h^{'''} (x_{1}) \approx 0,08 > 0$ und $h^{'''} (x_{2}) \approx - 2,65 < 0$ , liegen bei $x_{1}$ und $x_{2}$ jeweils Wendestellen vor.
Berechne den Wert der maximalen Steigung in einem der Wendepunkte von $G_{h}$
Für ein Maximum gilt allgemein: $h^{'} (x_{M}) = 0$ und $h^{''} (x_{M}) < 0$ .
Die betrachtete Funktion ist hier $h^{'} (x)$ .
Für ein Maximum der Steigung ergibt sich dann die folgende Bedingung: $h^{''} (x_{M}) = 0$ und $h^{'''} (x_{M}) < 0$ .
Berechnet wurde bereits $h^{'''} (\sqrt{3} - 2) \approx - 2,65$ .
Wegen $h^{'''} (\sqrt{3} - 2) < 0$ muss bei $x_{2}$ ein Hochpunkt des Graphen der Steigung $h^{'} (x)$ vorliegen, analog hat der Graph $h^{'}$ bei $x_{1}$ einen Tiefpunkt.
Berechne $h^{'} (\sqrt{3} - 2)$ :
Der Wert der maximalen Steigung von $G_{h}$ in dem Wendepunkt mit der x-Koordinate $x_{2} = \sqrt{3} - 2$ , beträgt rund $1,12$ .
Teil 1
Löse die Gleichung $h^{''} (x) = 0$ . $\Rightarrow x_{1}$ und $x_{2}$
Überprüfe $h^{'''} (x_{1})$ und $h^{'''} (x_{2})$ .
Teil 2
Für ein Maximum der Steigung ergibt sich die folgende Bedingung: $h^{''} (x_{M}) = 0$ und $h^{'''} (x_{M}) < 0$ .
Vergleiche mit den Ergebnissen für $h^{'''} (x)$ aus Teil 1.
(i) Der globale Hochpunkt $H$ von $G_{h}$ liegt im Intervall $[0; 1]$ .
Geben Sie seine Koordinaten an. (2 P)
(ii) $G_{h}$ schließt mit der $x$ -Achse eine Fläche $A$ ein. Die Gerade $k$ verläuft parallel zur $y$ -Achse durch $H$ und teilt die Fläche $A$ in zwei Teilflächen.
Berechnen Sie den Anteil, den die größere der beiden Teilflächen an der Fläche $A$ hat.
(4 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
(i) Gib die Koordinaten des Hochpunktes $H$ von $G_{h}$ an
Es ist $h^{'} (x) = e^{x} (- x^{2} - 2 x + 1)$ .
Löse die Gleichung $h^{'} (x) = 0$ :
Der CAS-Rechner liefert die beiden Lösungen $x_{1} = - \sqrt{2} - 1$ und $x_{2} = \sqrt{2} - 1$ .
Berechne $h^{''} (- \sqrt{2} - 1) \approx 0,25 > 0 \Rightarrow$ TP an der Stelle $x_{1}$ .
Berechne $h^{''} (\sqrt{2} - 1) \approx - 4,28 < 0 \Rightarrow$ HP an der Stelle $x_{2}$ .
Berechne $h (x_{2}) = (2 \cdot \sqrt{2} - 2) \cdot e^{\sqrt{2} - 1}$
Dann hat der Hochpunkt die Koordinaten: $H P (\sqrt{2} - 1 | (2 \cdot \sqrt{2} - 2) \cdot e^{\sqrt{2} - 1}) \approx H P (0,414 | 1,254)$ .
(ii)Berechne den Anteil, den die größere der beiden Teilflächen an der Fläche $A$ hat
Für die Nullstellen von $h$ gilt: $h (x) = 0 \Leftrightarrow x = - 1$ oder $x = 1$ .
Der Inhalt der Fläche $A$ entspricht dem Wert des Integrals $\int_{- 1}^{1} h (x) d x$ .
Die beiden Flächen $A_{1}$ und $A_{2}$
Zur Veranschaulichung wurde die obige Zeichnung angefertigt.
Man erkennt, dass die größere Fläche die Fläche $A_{2}$ ist.
Dies kann auch berechnet werden:
$A = \int_{- 1}^{1} h (x) d x \approx 1,47$
$A_{2} = \int_{- 1}^{- 1 + \sqrt{2}} h (x) d x \approx 0,95$
$A_{1} = A - A_{2} = 1,47 - 0,95 = 0,52 \Rightarrow$ die größere Fläche ist die Fläche $A_{2}$ .
Gesucht ist also das Verhältnis $\frac{A_{2}}{A}$ :
$\frac{A_{2}}{A} = \frac{\int_{- 1}^{- 1 + \sqrt{2}} h (x) d x}{\int_{- 1}^{1} h (x) d x} \approx 0,647$
Der Anteil, den die größere der beiden Teilflächen an der Fläche $A$ hat, beträgt rund $64,7 %$ .
(i)
Löse die Gleichung $h^{'} (x) = 0$ . $\Rightarrow x_{1}$ und $x_{2}$
Berechne $h^{''} (x_{1})$ und $h^{''} (x_{2})$ und entscheide, an welche Stelle ein Hochpunkt liegt.
Berechne $h (x_{1} oder x_{2})$ und gib die Koordinaten des Hochpunktes an.
(ii)
Berechne die Flächen $A = \int_{- 1}^{1} h (x) d x$ und $A_{2} = \int_{- 1}^{- 1 + \sqrt{2}} h (x) d x$ und entscheide, welche der beiden Teilflächen $A_{1}$ oder $A_{2}$ die größere ist.
Berechne dann $\frac{A_{größere}}{A}$ .
Für $0 < w < 1$ wird das Dreieck mit den Eckpunkten $(0 | 0), (w | 0)$ und $(w | h (w))$ betrachtet. Für einen Wert von $w$ ist der Flächeninhalt des Dreiecks maximal.
Berechnen Sie den maximalen Flächeninhalt, ohne dabei an Funktionsgraphen abgelesene Werte oder Zusammenhänge zu verwenden. (4 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
Berechne den maximalen Flächeninhalt, ohne dabei an Funktionsgraphen abgelesene Werte oder Zusammenhänge zu verwenden
Der Flächeninhalt berechnet sich für $0 < w < 1$ mittels der Funktion $i$ mit $i (w) = \frac{1}{2} \cdot w \cdot h (w) = \frac{1}{2} \cdot w \cdot (1 - w^{2}) \cdot e^{w}$ .
Löse die Gleichung $i^{'} (w) = 0$ .
Die Gleichung $i^{'} (w) = 0$ hat für $0 < w < 1$ nur die Lösung $w_{1}$ mit $w_{1} \approx 0,68$ .
Berechne $i^{''} (0,68)$ :
Wegen $i^{''} (0,68) \approx - 4,43 < 0$ liegt dort als einzige Extremstelle im Bereich $0 < w < 1$ das absolute Maximum vor.
Berechne $i (0,68)$ :
Aus $i (0,68) \approx 0,36$ folgt:
Der maximale Flächeninhalt beträgt etwa $0,36 FE$ .
Die folgende Abbildung ist nicht in der Aufgabenstellung gefordert. Sie dient nur zur Veranschaulichung.
Der Flächeninhalt berechnet sich für $0 < w < 1$ mittels der Funktion $i$ mit $i (w) = \frac{1}{2} \cdot w \cdot h (w)$ .
Für die Bestimmung des Extremums löse die Gleichung $i^{'} (w) = 0$ . Diese Gleichung hat für $0 < w < 1$ nur die Lösung $w_{1}$ .
Für den Nachweis des Maximums berechne $i^{''} (w_{1})$ .
Der maximale Flächeninhalt ist dann $i (w_{1})$ .

Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen → Was bedeutet das? serlo.org

Teil B: Analysis 1

Aufgabe 2

Begründe anhand des Funktionsterms, dass der Funktionswert h(x) nur für −1<x<1 positiv ist

Bestimme die x-Koordinate von Q gerundet auf zwei Nachkommastellen

Berechne die Wendestellen von h, ohne dabei an Funktionsgraphen abgelesene Werte oder Zusammenhänge zu verwenden

Berechne den Wert der maximalen Steigung in einem der Wendepunkte von Gh

(i) Gib die Koordinaten des Hochpunktes H von Gh an

(ii)Berechne den Anteil, den die größere der beiden Teilflächen an der Fläche A hat

Berechne den maximalen Flächeninhalt, ohne dabei an Funktionsgraphen abgelesene Werte oder Zusammenhänge zu verwenden

Begründe anhand des Funktionsterms, dass der Funktionswert $h (x)$ nur für $- 1 < x < 1$ positiv ist

Bestimme die x-Koordinate von $Q$ gerundet auf zwei Nachkommastellen

Berechne die Wendestellen von $h$ , ohne dabei an Funktionsgraphen abgelesene Werte oder Zusammenhänge zu verwenden

Berechne den Wert der maximalen Steigung in einem der Wendepunkte von $G_{h}$

(i) Gib die Koordinaten des Hochpunktes $H$ von $G_{h}$ an

(ii)Berechne den Anteil, den die größere der beiden Teilflächen an der Fläche $A$ hat