B I

In einem kartesischen Koordinatensystem des IR3 sind die Punkte $A (2 | 1 | 0)$ , $B (- 4 | 3 | 2)$ , $C (- 2 | 2 | 2)$ und die Punktemenge $D_{k} (k | 2 k | - 1)$ mit $k \in ℝ$ sowie die Gerade $g : \vec{x} = (\begin{array}{c} 1 \\ 0 \\ - 2 \end{array}) + r \cdot (\begin{array}{c} 0 \\ 1 \\ 1 \end{array})$ mit r $\in ℝ$ gegeben.

Überprüfen Sie, ob es ein $k \in ℝ$ gibt, so dass die Punkte $A, B, C$ und $D_{k}$ Eckpunkte des abgebildeten Trapezes sein können.
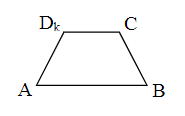
Die drei Punkte $A, B$ und $C$ spannen die Ebene $E$ auf. Bestimmen Sie je eine Gleichung der Ebene $E$ in Parameter- und Koordinatenform.
[ mögliches Teilergebnis: $E : x_{1} + 2 x_{2} + x_{3} - 4 = 0$ ]
Prüfen Sie durch Rechnung, ob es einen Wert für $k$ gibt, für den ein Punkt der Punktemenge $D_{k}$ sowohl in $E$ als auch in $g$ liegt.
Bestimmen Sie die Achsenschnittpunkte der Ebene $E$ und erstellen Sie eine Schrägbildskizze der Ebene $E$ im Koordinatensystem.
Die Ebene $E$ schließt mit den Koordinatenebenen eine Pyramide ein. Berechnen Sie die Maßzahl des Pyramidenvolumens.
Die Ebene $E$ und die $x_{1} - x_{2} -$ Koordinatenebene schneiden sich in der Geraden $h$ . Bestimmen Sie die gegenseitige Lage von $g$ und $h$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org