Teil 2 Analysis 1

Nach Öffnung einer Schleuse gibt für $t \geq 0$ die Funktion $w$ mit

$w (t) = \frac{e^{2 t} + 60 e^{t} - 60}{e^{2 t} + 10 e^{t} + 25}$

die zeitliche Entwicklung des Wasserdurchflusses in einem Kanal an einer Messstelle an. Der Wasserdurchfluss ist das Volumen des Wassers in $m^{3},$ das an dieser Stelle pro Sekunde vorbeifließt. Die Zeit $t$ wird ab Öffnung der Schleuse zum Zeitpunkt $t = 0$ in Sekunden gemessen. Die Abbildung zeigt einen Ausschnitt des Graphen $G_{w}$ der Funktion $w$ .

Bei allen Rechnungen kann auf das Mitführen von Einheiten verzichtet werden. Runden Sie alle Ergebnisse auf zwei Nachkommastellen.

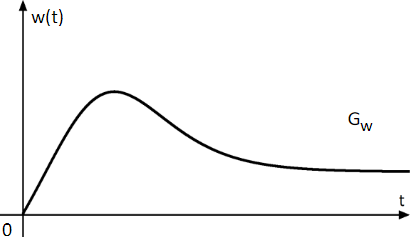
Geben Sie den Wasserdurchfluss eine Sekunde nach Öffnung der Schleuse und für $t \to \infty$ an.
Berechnen Sie den Zeitpunkt, zu dem der Wasserdurchfluss erstmals seit Beginn der Beobachtung den Wert von $1,0 \frac{m^{3}}{s}$ überschreitet.
Zeigen Sie, dass die Funktion $w$ auch durch die Gleichung
$w (t) = \frac{e^{2 t} + 60 e^{t} - 60}{(e^{t} + 5)^{2}}$
dargestellt werden kann.
Berechnen Sie die Koordinaten des Hochpunktes von $G_{w}$ und interpretieren Sie diese im Sachzusammenhang. Hinweis: Der Nachweis, dass ein Hochpunkt vorliegt, muss nicht erbracht werden.
[ Mögliches Teilergebnis: $w (t) = \frac{- 50 e^{2 t} + 420 e^{t}}{(e^{t} + 5)^{3}}$ ]

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org