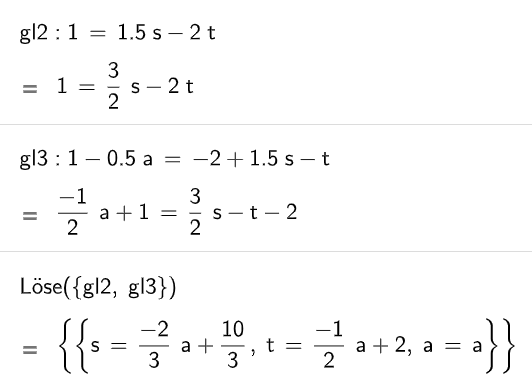Wahlteil - GTR
Aufgabe 3C
In einem Koordinatensystem mit Ursprung sind die folgenden Vektoren gegeben:
und
Zeigen Sie die Gültigkeit folgender Aussagen:
Es gibt Werte für und , sodass gilt:
und sind nicht kollinear.
(4BE)
Die Gerade durch die Punkte und wird mit bezeichnet.
Die Gerade durch die Punkte und wird mit bezeichnet.
Begründen Sie nur mit den Aussagen aus Teilaufgabe a), dass sich und in genau einem Punkt schneiden. (3BE)
Die Geraden und liegen in der Ebene mit der Gleichung
.
Für jeden Wert von wird ein Punkt betrachtet.
Geben Sie eine Gleichung der Geraden durch und an. (2BE)
Zeigen Sie, dass der Punkt für jeden Wert von in der Ebene liegt. (4BE)
Berechnen Sie den Wert von , sodass sich die Gerade und die Gerade durch die Punkte und orthogonal schneiden. (3BE)
Bestimmen Sie den Wert von , für den der Abstand von und minimal ist. (4BE)