Nachtermin Teil B

Aufgabe B2

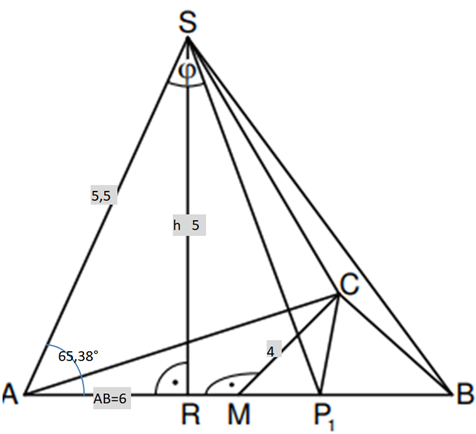
Das gleichschenklige Dreieck $A B C$ mit der Basis $A B$ ist die Grundfläche der Pyramide $A B C S$ mit der Höhe $R S (R \in A B)$ .

Der Punkt $M$ ist der Mittelpunkt der Basis $A B$ .

Es gilt: $A B = 6 cm$ ; $M C = 4 cm$ ;

$A S = 5,5 cm$ ; $R S = 5 cm$ .

Die Zeichnung zeigt ein Schrägbild der Pyramide $A B C S$ .

In der Zeichnung gilt:

$q = \frac{1}{2}$ ; $ω = 45^{\circ}$ ; $A B$ liegt auf der Schrägbildachse.

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

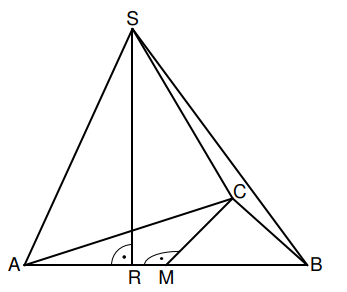
Berechnen Sie das Maß des Winkels $B A S$ . (1 P)
$[$ Ergebnis: $∢ B A S = {65,38}^{\circ}]$

geg.: $△ A B C$ gleichschenklig mit Basis $A B = 6 c m$ , als Grundfläche der Pyramide ABCS,
$h_{P y r a m i d e} = R S = 5 c m$ (mit $R \in A B$ , $M =$ Mittelpunkt $A B$ ;
Schrägbild mit Schrägbildachse $A B$ , mit $q = 0,5$ und $ω = 45 °$ ;
$| M C | = 4 c m$ ; $| A S | = 5,5 c m$ ;
ges.: Zeichnung aus Aufgabenstellung ergänzen, $∢ B A S$ berechnen
Ansatz und Rechnung:
1. Schrägbild der Pyramide ergänzen:
Schrägbild Pyramide ABCS
2. Winkel BAS berechnen:
aus Zeichnung $∢ B A S ≙ ∢ R A S$ ; Berechnung $∢ B A S$ mithilfe Sinus
$\Rightarrow \sin ∢ B A S = [\frac{G K}{H Y}] = \frac{R S}{A S} = \frac{5}{5,5} = 0,9090$
$\Rightarrow ∢ 𝐁 𝐀 𝐒 = 𝟔𝟓,𝟑𝟖 °$
Zeichnung mit gegebenen Werten ergänzen und Winkel BAS berechnen
Punkte $P_{n}$ liegen auf der Strecke $A B$ . Die Winkel $A S P_{n}$ haben das Maß $φ$ mit
$φ \in] 0^{\circ}; {61,18}^{\circ}]$ .
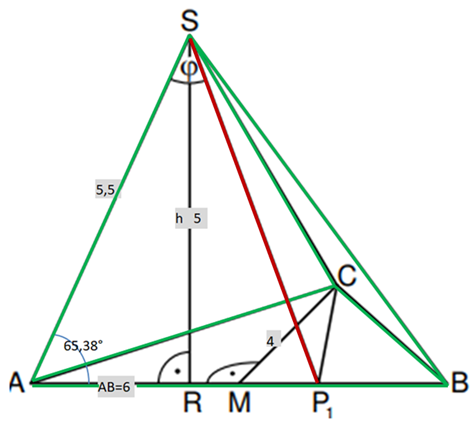
Zeichnen Sie die Strecke $S P_{1}$ für $φ = 45^{\circ}$ in das Schrägbild zur Aufgabenstellung ein.
Zeigen Sie sodann, dass für die Länge der Strecken $S P_{n}$ in Abhängigkeit von $φ$ gilt:
$| S P_{n} | (φ) = \frac{5}{\sin ({65,38}^{\circ} + φ)} cm .$ (2,5 P)

geg.: $∢ A S P_{n} = φ$ mit $φ \in] 0 °; 61,18 °]$
ges.:
1. Einzeichnung Strecke $S P_{1}$ für $φ = 45 °$ in das Schrägbild der Pyramide
2. Berechnung $S P_{n} (φ)$ mit Sinus-Supplementwinkel-Beziehung
Ansatz und Rechnung:
1. Schenkel in $S$ mit $45 °$ an Strecke $A S$ schneidet Strecke $A B$ in $P_{1}$
Schrägbild Pyramide mit Strecke $S P_{1}$
2. Berechnung $S P_{n} (φ)$ mit Sinus-Supplementwinkel-Beziehung
$\sin (180 ° - (φ + ∢ B A S)) = \frac{| R S |}{| S P_{n} |} = \frac{5 c m}{| S P_{n} |}$ für $φ \in] 0 °; 61,18 °]$
Entsprechend der Supplementwinkel-Beziehung $\sin (180 ° - α) = \sin (α)$
ergibt sich für $\sin (180 ° - (φ + ∢ B A S)) = \sin (φ + ∢ B A S)$
$\Rightarrow \sin (φ + 65,38 °) = \frac{5 c m}{| S P_{n} |}$
nach Äquivalenzumformung (Multiplikation mit $| S P_{n} |$ und Division durch $\sin (φ + 65,38 °)$ ) folgt
$| 𝐒 𝐏_{𝐧} | (𝛗) = \frac{𝟓}{\sin (𝛗 + 𝟔𝟓,𝟑𝟖 °)} 𝐜 𝐦$
Pyramide mit gegebenen Werten ergänzen,
Streckenberechnung mithilfe der Sinus-Supplementwinkel-Beziehung
Die Dreiecke $A P_{n} S$ sind die Grundflächen von Pyramiden $A P_{n} S C$ mit der Spitze $C$ .
Zeichnen Sie die Pyramide $A P_{1} S C$ in die Zeichnung zur Aufgabenstellung ein.
Berechnen Sie sodann das Volumen $V$ der Pyramiden $A P_{n} S C$ in Abhängigkeit von $φ$ . (2,5 P)

ges.:
1. Pyramide $A P_{1} S C$ mit C als Spitze $\Rightarrow h ≙ | M C | = 4 c m$
2. . Volumen $V (φ)$ der Pyramiden $A P_{n} S C$
Ansatz und Rechnung:
1. Pyramide $A P_{1} S C$ siehe Skizze in Aufgabe B a)
2. Volumen der Pyramiden $A P_{n} S C$
$𝐕_{Pyr} = \frac{𝟏}{𝟑} \cdot 𝐆_{𝐀 𝐏_{𝐧} 𝐒} \cdot 𝐡$
$G_{A P_{n} S}$ mithilfe Sinussatz: $𝐆 = \frac{𝟏}{𝟐} \cdot 𝐜 \cdot 𝐛 \cdot \sin (𝛂)$
$\Rightarrow G_{A P_{n} S} = \frac{1}{2} \cdot | A S | \cdot | S P_{n} | (φ) \cdot \sin (φ)$
mit $h ≙ M C = 4 c m$ , $| A S | = 5,5 c m$ und $| S P_{n} | (φ) = \frac{5}{\sin (65,38 ° + φ)} c m$
eingestzt in $V_{Pyr}$ ergibt das
$\Rightarrow V_{Pyr} (φ) = \frac{1}{3} \cdot \frac{1}{2} \cdot | A S | \cdot | S P_{n} | (φ) \cdot \sin (φ) \cdot 4$
$\Rightarrow V_{Pyr} (φ) = \frac{1}{3} \cdot \frac{1}{2} \cdot 5,5 \cdot \frac{5}{\sin (65,38 ° + φ)} \cdot \sin (φ) \cdot 4 [c m^{3}]$ mit $φ \in] 0 °; 61,18 °]$
$\Rightarrow 𝐕_{Pyr} (𝛗) = 𝟏𝟖,𝟑𝟑 \cdot \frac{𝐬 𝐢 𝐧 (𝛗)}{\sin (𝟔𝟓,𝟑𝟖 ° + 𝛗)} [c m^{3}]$
Pyramide $A P_{1} S C$ zeichnen und Volumen $V (φ)$ berechnen

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das? serlo.org