Nachtermin Teil B

Aufgabe B1

Pfeile $\vec{O P_{n}} (φ) = (\begin{array}{c} 5 - \sin φ \\ 2 \cdot \cos φ \end{array})$ und $\vec{O Q_{n}}$ mit $O (0 | 0)$ spannen für $φ \in [0^{\circ}; 360^{\circ}]$ gleichschenklige Dreiecke $O P_{n} Q_{n}$ mit den Basen $P_{n} Q_{n}$ auf. Die Gerade $s$ mit der Gleichung $y = x (x, y \in ℝ)$ ist die Symmetrieachse der Dreiecke $O P_{n} Q_{n}$ .

In das Koordinatensystem ist das Dreieck $O P_{1} Q_{1}$ für $φ = 60^{\circ}$ bereits eingezeichnet.

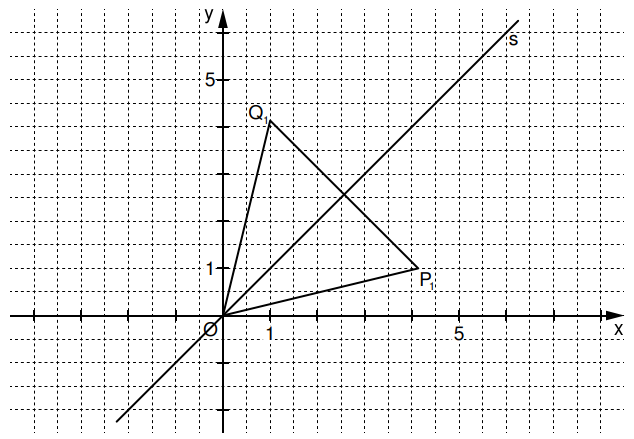
Geben Sie die Koordinaten des Pfeils $\vec{O P_{2}}$ für $φ = 220^{\circ}$ an und zeichnen Sie das Dreieck $O P_{2} Q_{2}$ in die Zeichnung zur Aufgabenstellung ein.
Runden Sie auf eine Nachkommastelle. (2 P)

geg.: gleichschenkliges Dreieck $O P_{1} Q_{1}$ mit $φ = 60 °$ und Symmetrieachse $S : y = x$
ges.: Koordinaten $\vec{O P_{2}}$ und Zeichnung $△ O P_{2} Q_{2}$ für $φ = 220^{\circ}$
Ansatz und Rechnung:
1. Koordinaten von $\vec{O P_{2}} (φ = 220^{\circ})$
$\vec{O P_{2}} (φ = 220^{\circ}) = (\begin{array}{c} 5 - \sin (220 °) \\ 2 \cdot \cos (220 °) \end{array}) \approx (\begin{array}{c} 5 - (- 0,643) \\ 2 \cdot (- 0,766) \end{array})$
$= (\begin{array}{c} 5,643 \\ - 1,532 \end{array}) \approx (\begin{array}{c} 5,6 \\ - 1,5 \end{array})$
2. Zeichnung $△ O P_{2} Q_{2}$
$\vec{O P_{2}} (φ = 220^{\circ}) = (\begin{array}{c} 5,6 \\ - 1,5 \end{array})$ einzeichnen; $Q_{2}$ symmetrisch zur Symmetrieachse $S : y = x$
Zeichnung der Dreiecke $O P_{1} Q_{1}$ mit $φ = 60 °$ und $O P_{2} Q_{2}$ mit $φ = 220 °$
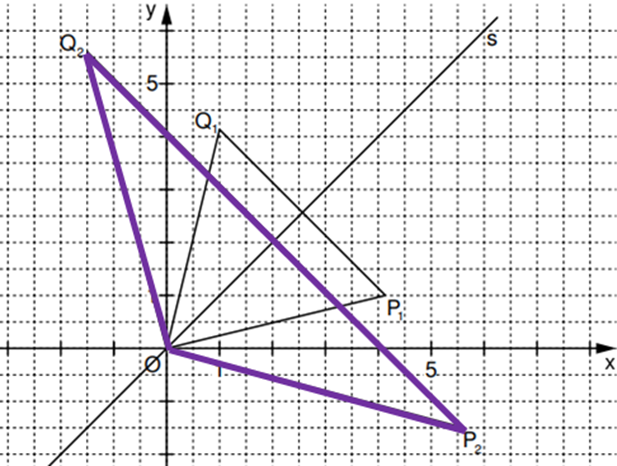
Skizze mit dem Dreieck $O P_{2} Q_{2}$ .
Koordinaten berechnen, gleichschenkliges Dreieck zeichnen
Für die Dreiecke $O P_{3} Q_{3}$ und $O P_{4} Q_{4}$ gilt: $∢ P_{3} O Q_{3} = ∢ P_{4} O Q_{4} = 90^{\circ}$ .
Bestimmen Sie die zugehörigen Werte von $φ$ . (2 P)

geg.: gleichschenklige Dreiecke $O P_{3} Q_{3}$ und $O P_{4} Q_{4}$ mit $∢ P_{3} O Q_{3} = ∢ P_{4} O Q_{4} = 90^{\circ}$
ges.: Wert $φ$
Ansatz & Rechnung
Setze für beide Dreiecke $O P_{3} Q_{3}$ und $O P_{4} Q_{4}$ die $y$ -Komponente von $\vec{O P_{n}} (φ) = (\begin{array}{c} 5 - \sin φ \\ \blue 2 \cdot \cos φ \end{array})$ gleich null:
$y_{P 3, P 4} = 0 = \blue 2 \cdot \cos φ$ für $φ \in [0 °; 360 °]$
$\Rightarrow$ im Bereich $φ \in [0 °; 360 °]$ ist die Gleichung erfüllt für $c o s (\frac{π}{2}) ≙ 0$ und für $c o s (\frac{3}{2} π) ≙ 0$
Damit muss $φ = 90 °$ oder $φ = 270 °$ sein.
$𝕃 = {90^{\circ}; 270^{\circ}}$
Bestimme $φ$ durch den Vektor $O P_{n} (φ)$ . Wenn der Winkel im Punkt $O$ $90^{\circ}$ ist, dann muss der Vektor auf der x-Achse liegen. Setze also den $y$ -Wert des Vektors gleich 0.
Begründen Sie, weshalb es unter den Dreiecken $O P_{n} Q_{n}$ kein Dreieck $O P_{5} Q_{5}$ mit $P_{5} (3 | 3)$ gibt. (1 P)

Nachweis
Der Punkt $P_{5} (3 | 3)$ liegt auf der Symmetrieachse, die durch $y = x$ gegeben ist.
Wenn $P_{5} (3 | 3)$ auf der Symmetrieachse $s$ liegt, liegen auch $Q_{5}$ und $O$ darauf. Das ergibt kein Dreieck.
$\Rightarrow$ Es gibt kein Dreieck $O P_{5} Q_{5}$ mit $P_{5} (3 | 3)$
Skizziere den Punkt in das Koordinatensystem.

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das? serlo.org

Nachtermin Teil B

Aufgabe B1

Ansatz & Rechnung

Nachweis