Teil B

Aufgabe B4

Das Trapez $A B C D$ mit $A D ∥ B C$ ist die Grundfläche des Prismas $A B C D E F G H$ mit der Höhe $A E$ (siehe Skizze).

Es gilt: $A B = 5,5 cm$ ; $A D = 8 cm$ ;

$∢ B A D = 90^{\circ}$ ; $B C = 6 cm$ ; $A E = 9 cm$ .

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

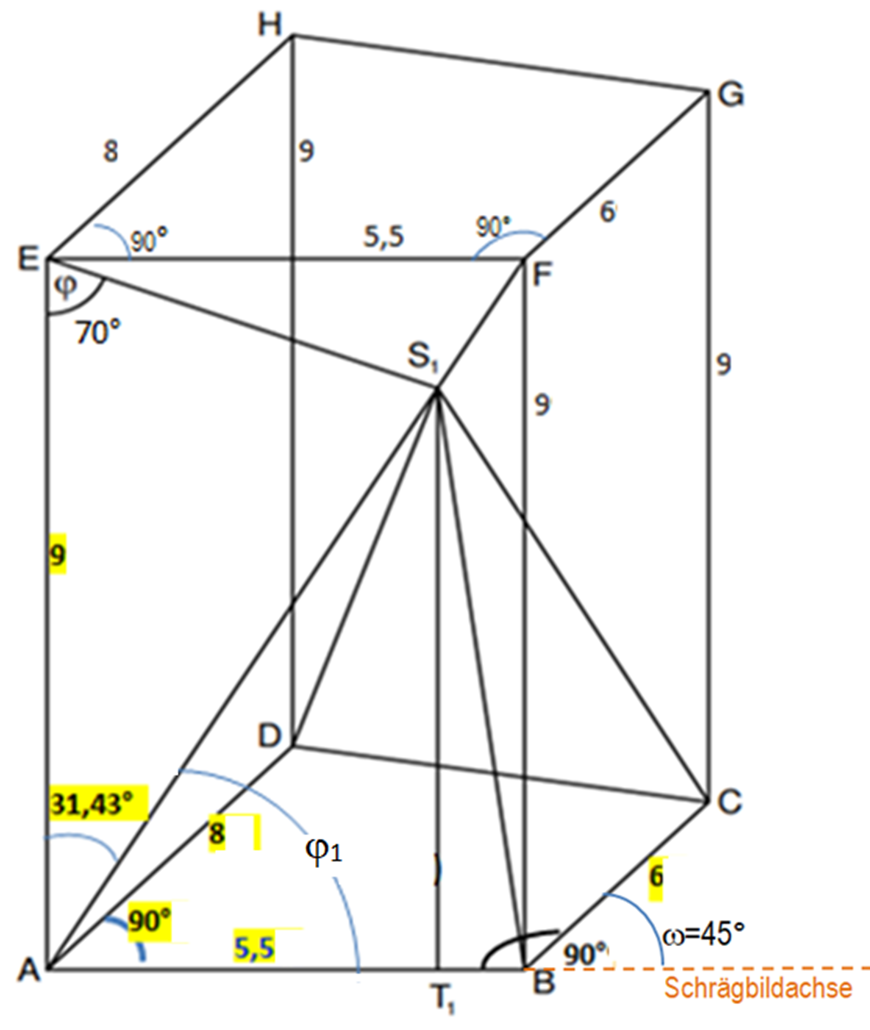
Zeichnen Sie das Schrägbild des Prismas $A B C D E F G H$ und die Strecke $A F$ , wobei die Strecke $A B$ auf der Schrägbildachse und der Punkt $A$ links vom Punkt $B$ liegen soll.
Für die Zeichnung gilt: $q = \frac{1}{2}$ ; $ω = 45^{\circ}$ .
Zeigen Sie sodann, dass für das Maß des Winkels $F A E$ gilt: $∢ F A E = {31,43}^{\circ}$ . (3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schrägbilder zeichnen
Zeichnung Schrägbild Prisma:
Berechnung $∢ F A E$ mithilfe des Tangens
(Im folgenden wird abgekürzt: AK: Ankathete, GK: Gegenkathete und HY: Hypotenuse)
$\tan (∢ F A E) = [\frac{G K}{A K}] = \frac{| E F |}{| A E |} = \frac{5,5 c m}{9 c m} = 0, 6$
$\Rightarrow ∢ F A E = 31,43 °$
Zeichne das Schrägbild des Prismas.
Berechne das Maß des Winkels $F A E$ mit dem Tangens.
Punkte $S_{n}$ liegen auf der Strecke $A F$ . Die Winkel $A E S_{n}$ haben das Maß $φ$ mit $φ \in] 0^{\circ}; 90^{\circ}]$ . Die Punkte $S_{n}$ sind die Spitzen von Pyramiden $A B C D S_{n}$ mit den Höhen $S_{n} T_{n}$ .
Es gilt: $T_{n} \in A B$ .
Zeichnen Sie für $φ = 70^{\circ}$ die Strecke $E S_{1}$ , die Pyramide $A B C D S_{1}$ und die Höhe $S_{1} T_{1}$ in das Schrägbild zu a) ein.
Ermitteln Sie sodann rechnerisch die Länge der Strecken $A S_{n}$ in Abhängigkeit von $φ$ .
(3,5 P)
$[$ Teilergebnis: $| A S_{n} (φ) | = \frac{9 \cdot \sin φ}{\sin (φ + {31,43}^{\circ})} cm]$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinussatz und Kosinussatz im allgemeinen Dreieck
Zeichnung
$φ = 70 °$ an $A E$ antragen, schneidet $A F$ in $S_{1}$ ;
$S_{1}$ mit den Eckpunkten $A, B, C, D$ verbinden;
Höhe durch $S_{1}$ $⊥$ zur Strecke $A B$ zeichnen
Berechnung der Strecke $| A S_{n} |$ mithilfe der Verhältnisgleichung der Strecken $| A S_{n} |$ und $| A E |$ und deren Sinus
Dafür halten wir fest, dass der Winkel gegenüber $| A S_{n} |$ $φ$ beträgt.
Den Winkel gegenüber $| A E |$ berechnen wir mithilfe der Innenwinkelsumme eines Dreiecks: $180 - (φ + 31,43)$
$\frac{| A S_{n} |}{| A E |}$ $=$ $\frac{\sin φ}{\sin (180 ° - (φ + 31,43))}$ $\cdot | A E |$
$| A S_{n} |$ $=$ $\frac{| A E | \cdot \sin φ}{\sin (180 ° - (φ + 31,43))}$
↓
$| A E |$ einsetzen
$| A S_{n} |$ $=$ $\frac{9 \cdot \sin φ}{\sin (180 ° - (φ + 31,43))}$
Ergänze die Pyramide in deiner Zeichnung.
Berechne die Strecke $| A S_{n} |$ mit dem Sinussatz.

In der Pyramide $A B C D S_{2}$ gilt: $| A T_{2} | = 3,5 cm$ .

Berechnen Sie die Länge der Strecke $A S_{2}$ sowie den zugehörigen Wert für $φ$ . (3,5 P)

$[$ Teilergebnis: $| A S_{2} | = 6,71 cm]$

Zeigen Sie durch Rechnung, dass für das Volumen $V$ der Pyramiden $A B C D S_{n}$ in
Abhängigkeit von $φ$ gilt: $V (φ) = \frac{98,56 \cdot \sin φ}{\sin (φ + {31,43}^{\circ})} {cm}^{3}$ . (3 P)
Volumen der Pyramide
Allgemein gilt:
$V_{Pyr} = \frac{1}{3} \cdot G_{Trapez A B C D} \cdot h_{Pyramide A B C D S_{n}}$
mit $G_{Trapez A B C D} = \frac{1}{2} \cdot (| A D | + | B C |) \cdot | A B |$ und
mit $h_{Pyramide A B C D S_{n}} = | S_{n} T_{n} |$
$\Rightarrow V_{P y r} = \frac{1}{3} \cdot \frac{1}{2} \cdot (| A D | + | B C |) \cdot | A B | \cdot | S_{n} T_{n} |$
Bekannt ist schon:
$| A D | = 8 c m$
$| B C | = 6 c m$
$| A B | = 5,5 c m$
Die noch fehlende Größe $| S_{n} T_{n} |$ wird berechnet
$\sin (90 ° - 31,43 °) = [\frac{G K}{H Y}] = \frac{| S_{n} T_{n} |}{| A S_{n} |}$
Hierbei sind $| A S_{n} | = \frac{9 \cdot \sin φ}{\sin (φ + 31,43 °)}$ (vgl. Aufgabe 4 b)
und $\sin (90 ° - 31,43 °) = \sin (58,57 °) \approx 0,853$
Damit wird
$| S_{n} T_{n} | = 0,853 \cdot | A S_{n} | = 0,853 \cdot \frac{9 \cdot \sin φ}{\sin (φ + 31,43 °)} = 7,68 \cdot \frac{\sin φ}{\sin (φ + 31,43 °)}$
Wir setzen $| S_{n} T_{n} |$ in die vorher aufgestellte Formel ein
$\Rightarrow V_{Pyr} = \frac{1}{3} \cdot \frac{1}{2} \cdot (8 + 6) \cdot 5,5 \cdot 7,68 \cdot \frac{\sin φ}{\sin (φ + 31,43 °)}$
$\Rightarrow V_{Pyr (φ)} = 98,56 \cdot \frac{\sin φ}{\sin (φ + 31,43 °)}$
Berechne des Volumens $V$ der Pyramide $A B C D S_{n}$ .
Bestimme dazu die Länge $| S_{n} T_{n} |$ mit dem Sinus.
Unter den Strecken $E S_{n}$ hat die Strecke $E S_{0}$ die minimale Länge.
Begründen Sie, dass für die zugehörige Belegung für $φ$ gilt: $φ = {58,57}^{\circ}$ .
Berechnen Sie sodann den prozentualen Anteil des Volumens der Pyramide $A B C D S_{0}$ am Volumen des Prismas $A B C D E F G H$ . (3,5 P)
%
Berechne $φ$ im Dreieck $A E S_{0}$ : es gilt $φ = 180 ° - 90 ° - 31,43 ° = 58,57 °$
Nun berechnen wir das Volumen mit der Formel aus d
Dafür setzen wir $φ = 58,57 °$ in die Gleichung aus d ein:
$98,56 \cdot \frac{\sin φ}{\sin (φ + 31,43 °)}$
↓
Wert $φ = 58,57 °$ einsetzen
$=$ $98,56 \cdot \frac{\sin (58,57 °)}{\sin (58,57 ° + 31,43 °)}$
$=$ $98,56 \cdot \frac{\sin (58,57 °)}{\sin (90 °)}$
$=$ $98,56 \cdot \frac{0,853}{1}$
$=$ $84,07 c m^{3}$
Jetzt berechnen wir das Gesamtvolumen des Prismas
Hierfür nutzen wir die berechneten Werte aus d
$V_{Prisma} = G \cdot h = \frac{1}{2} \cdot (| A D | + | B C |) \cdot | A B | \cdot h$
$V_{Prisma} = \frac{1}{2} \cdot (8 + 6) \cdot 5,5 \cdot 9 c m^{3}$
$V_{Prisma} = 346,5 c m^{3}$
Zuletzt berechnen wir mit den beiden Volumen den prozentualen Anteil
$\frac{V_{(Pyr)}}{V_{(Prisma)}} = \frac{84,10 c m^{3}}{346,5 c m^{3}} = 0,2427 ≙ 24,27 %$
Überlege dir, wie groß der Winkel $φ$ sein muss, damit $E S_{0}$ eine minimale Länge annimmt.
Setze dieses Winkelmaß $φ$ in die Volumenformel aus Aufgabenteil d ein.
Berechne danach das Volumen des Prismas $A B C D E F G H$ , sowie den prozentualen Anteil der Pyramide am Volumen des Prismas.

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das? serlo.org

$\cos φ$	$=$	$\frac{AK}{HY}$
$\cos (90 ° - 31,43 °)$	$=$	$\frac{3,5 cm}{A S_{2}}$
	↓	auflösen nach $A S_{2}$
$\| A S_{2} \|$	$=$	$\frac{3,5 cm}{\cos (58,57 °)}$
$\| A S_{2} \|$	$=$	$6,71$

$6,71$	$=$	$\frac{9 \cdot \sin φ}{\sin (φ + {31,43}^{\circ})}$
$\frac{6,71}{9}$	$=$	$\frac{\sin φ}{\sin (φ + {31,43}^{\circ})}$
	↓	mit Additionstheorem für Sinus: $\sin (α + β) = \sin α \cdot \cos β + \cdot \sin β \cdot \cos α$
$0,746$	$=$	$\frac{\sin φ}{\sin φ \cdot cos (31,43) + sin (31,43) \cdot \cos φ}$
$0,746$	$=$	$\frac{\sin φ}{\sin φ \cdot 0,85 + 0,52 \cdot \cos φ}$	$\cdot \sin ⁡ (φ) \cdot 0,853 + 0,521 \cdot \cos ⁡ (φ)$
$\sin ⁡ (φ)$	$=$	$0,746 \cdot [(\sin ⁡ (φ) \cdot 0,853 + 0,521 \cdot \cos ⁡ (φ)]$
$\sin ⁡ (φ)$	$=$	$0,636 \cdot \sin ⁡ (φ) + 0,389 \cdot \cos ⁡ (φ)$	$: \sin (φ)$
$1$	$=$	$\frac{0,636 \cdot \sin ⁡ (φ)}{\sin ⁡ (φ)} + \frac{0,389 \cdot \cos ⁡ (φ)}{\sin ⁡ ⁡ (φ)}$
	↓	$\sin ⁡ ⁡ (φ)$ im ersten Bruch kürzen
$1$	$=$	$0,636 + 0,389 \cdot \frac{\cos ⁡ (φ)}{\sin ⁡ (φ)}$
	↓	ersetze $\frac{\sin ⁡ (φ)}{\cos ⁡ (φ)} = \tan ⁡ (φ)$
$1$	$=$	$0,636 + 0,389 \frac{1}{\tan ⁡ (φ)}$	$0,636$
$0,364$	$=$	$0,389 \frac{1}{\tan ⁡ (φ)}$	$: 0,388$
$\frac{0,364}{0,389}$	$=$	$\frac{1}{\tan ⁡ (φ)}$
	↓	Kehrbruch
$\tan ⁡ (φ)$	$=$	$\frac{0,389}{0,363}$	${tan}^{- 1}$
$φ$	$=$	$\tan^{- 1} (\frac{0,389}{0,364}) = {46,90}^{\circ}$

Teil B

Aufgabe B4

Zeichnung Schrägbild Prisma:

Berechnung $∢ F A E$ mithilfe des Tangens

Zeichnung

Berechnung der Strecke $| A S_{n} |$ mithilfe der Verhältnisgleichung der Strecken $| A S_{n} |$ und $| A E |$ und deren Sinus

Länge der Strecke berechnen

Berechnung von $φ$ mit der allgemeinen Formel aus b

Volumen der Pyramide

Die noch fehlende Größe $| S_{n} T_{n} |$ wird berechnet

Wir setzen $| S_{n} T_{n} |$ in die vorher aufgestellte Formel ein

Nun berechnen wir das Volumen mit der Formel aus d

Jetzt berechnen wir das Gesamtvolumen des Prismas

Zuletzt berechnen wir mit den beiden Volumen den prozentualen Anteil

$\frac{\| A S_{n} \|}{\| A E \|}$	$=$	$\frac{\sin φ}{\sin (180 ° - (φ + 31,43))}$	$\cdot \| A E \|$
$\| A S_{n} \|$	$=$	$\frac{\| A E \| \cdot \sin φ}{\sin (180 ° - (φ + 31,43))}$
	↓	$\| A E \|$ einsetzen
$\| A S_{n} \|$	$=$	$\frac{9 \cdot \sin φ}{\sin (180 ° - (φ + 31,43))}$

	$98,56 \cdot \frac{\sin φ}{\sin (φ + 31,43 °)}$
	↓ Wert $φ = 58,57 °$ einsetzen
$=$	$98,56 \cdot \frac{\sin (58,57 °)}{\sin (58,57 ° + 31,43 °)}$
$=$	$98,56 \cdot \frac{\sin (58,57 °)}{\sin (90 °)}$
$=$	$98,56 \cdot \frac{0,853}{1}$
$=$	$84,07 c m^{3}$

Teil B

Aufgabe B4

Zeichnung Schrägbild Prisma:

Berechnung ∢FAE mithilfe des Tangens

Zeichnung

Berechnung der Strecke |ASn| mithilfe der Verhältnisgleichung der Strecken |ASn| und |AE| und deren Sinus

Länge der Strecke berechnen

Berechnung von φ mit der allgemeinen Formel aus b

Volumen der Pyramide

Die noch fehlende Größe |SnTn| wird berechnet

Wir setzen |SnTn| in die vorher aufgestellte Formel ein

Nun berechnen wir das Volumen mit der Formel aus d

Jetzt berechnen wir das Gesamtvolumen des Prismas

Zuletzt berechnen wir mit den beiden Volumen den prozentualen Anteil

Berechnung $∢ F A E$ mithilfe des Tangens

Berechnung der Strecke $| A S_{n} |$ mithilfe der Verhältnisgleichung der Strecken $| A S_{n} |$ und $| A E |$ und deren Sinus

Berechnung von $φ$ mit der allgemeinen Formel aus b

Die noch fehlende Größe $| S_{n} T_{n} |$ wird berechnet

Wir setzen $| S_{n} T_{n} |$ in die vorher aufgestellte Formel ein