Teil 1, Analysis

g ist eine ganzrationale Funktion vierten Grades mit der Definitionsmenge $D_{g} = ℝ$ .

In der Abbildung sehen Sie ausschnittsweise den Graphen der Ableitungsfunktion $g^{'}$ .

Ganzzahlige Werte können der Abbildung entnommen werden.

Geben Sie die Stellen an, an welchen der Graph der Funktion g Punkte mit horizontaler Tangente hat und benennen Sie jeweils die Art dieser Graphenpunkte. (2 BE)

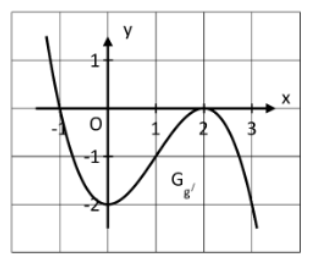
Nullstelle von $g^{'}$ bei $x = - 1$
Da der Graph von $g^{'}$ bei dieser Nullstelle das Vorzeichen wechselt, handelt es sich um eine Extremstelle.
Dass der Graph $G_{g^{'}}$ davor oberhalb der x-Achse verläuft, bedeutet, dass der Graph $G_{g}$ links von $x = - 1$ streng monoton steigt. Rechts von $x = - 1$ fällt der Graph von $G_{g}$ dann streng monoton, da $G_{g^{'}}$ unterhalb der x-Achse verläuft.
Es handelt sich deshalb um einen Hochpunkt.
Nullstelle von $g^{'}$ bei $x = 2$
An dieser Nullstelle wechselt der Graph $G_{g^{'}}$ nicht das Vorzeichen, sondern verläuft weiterhin unterhalb der x-Achse.
Das bedeutet, dass der Graph $G_{g}$ sowohl links von $x = 2_{}$ als auch rechts davon streng monoton fällt und bei $x = 2$ ein Terrassenpunkt von $G_{g}$ ist.
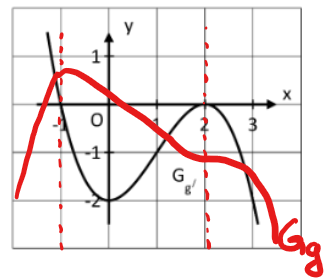
Mögliches Aussehen von $G_{g}$
Einen möglicher Graph von g siehst du unten im Koordinatensystem skizziert.
Zum Einen sind abseits der Punkte mit waagerechten Tangenten keine weiteren Steigungen verwendet worden, zum Anderen kann der Graph der Stammfunktion beliebig nach oben oder unten verschoben sein.
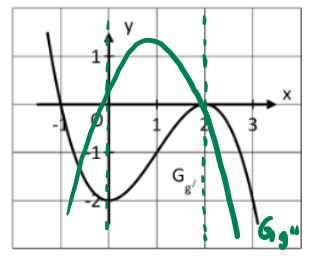
Hat der Graph von $g$ eine waagerechte Tangente in einem Punkt, so hat der Graph der Ableitung $g^{'}$ dort eine Nullstelle.
Je nachdem, ob $g^{'}$ an dieser Stelle das Vorzeichen wechselt, handelt es sich dann um einen Extrempunkt (Hoch- oder Tiefpunkt) oder um einen Terrassenpunkt.
Geben Sie mit Begründung die Wendestellen der Funktion g an. (3 BE)

$G_{g^{'}}$ hat Extremstellen bei $x = 0$ und $x = 2$ . Dort liegen also die Wendestellen von $G_{g}$ , da $G_{g^{''}}$ dort Nullstellen hat.
Mögliches Aussehen von $G_{g^{''}}$
Der Graph von g hat einen Wendepunkt, wenn $g^{''} (x) = 0$ (und der Graph $G_{g^{''}}$ dort das Vorzeichen wechselt).
Das ist genau dann der Fall, wenn Der Graph der Ableitungsfunktion $G_{g}$ einen Extrempunkt (keinen Terrassenpunkt!) hat.

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das? serlo.org

Teil 1, Analysis

Nullstelle von g′ bei x=−1

Nullstelle von g′ bei x=2

Mögliches Aussehen von Gg

Mögliches Aussehen von Gg′′

Nullstelle von $g^{'}$ bei $x = - 1$

Nullstelle von $g^{'}$ bei $x = 2$

Mögliches Aussehen von $G_{g}$

Mögliches Aussehen von $G_{g^{''}}$