Aufgaben zum Schnittwinkel von Geraden und Ebenen
Welchen Winkel schließen die Ebenen
und ein?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittwinkel in der analytischen Geometrie
Für die Berechnung des Schnittwinkels der beiden Ebenen gilt folgende Formel:
Du benötigst also von den Ebenen die Normalenvektoren und deren Beträge.
Die Ebene liegt in der Parameterform vor. Der Normalenvektor der Ebene muss also berechnet werden.
Dazu gibt es zwei Möglichkeiten:
Berechnung des Normalenvektors über das Vektorprodukt der beiden Richtungsvektoren.
Der Normalenvektor steht senkrecht auf den beiden Richtungsvektoren. Das Skalarprodukt zwischen dem Normalenvektor und jedem Richtungsvektor ist gleich null.
Möglichkeit 1
Möglichkeit 2
und
Wird jeweils das Skalarprodukt berechnet, so erhältst du zwei Gleichungen.
Aus Gleichung folgt
Bei zwei Gleichungen mit drei Unbekannten ist eine Variable frei wählbar.
Setze z.B. . Dann ist auch gleich .
Mit Gleichung folgt dann:
Damit ist .
Der Normalenvektor der Ebene kann abgelesen werden.
Berechne nun die Beträge der beiden Normalenvektoren.
Setze in die Formel für die Winkelberechnung ein:
Du hast die Gleichung erhalten.
Durch Anwendung der Umkehrfunktion des Kosinus kannst du den Winkel berechnen. Benutze auf dem Taschenrechner die Funktion .
Antwort: Der Schnittwinkel zwischen den beiden Ebenen beträgt .
Zusätzliche graphische Darstellung, die in der Aufgabenstellung nicht gefordert ist
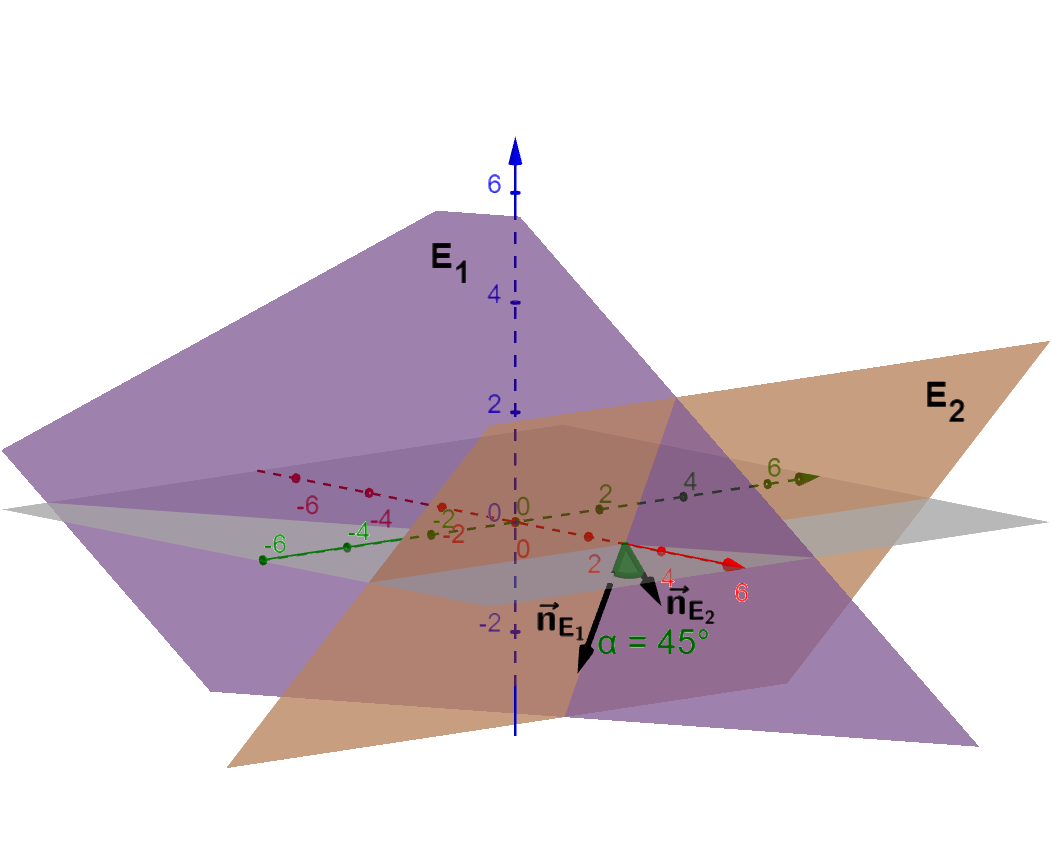
Berechne zuerst den Normalenvektor der Ebene . Verwende anschließend die Formel des Schnittwinkels zweier Vektoren (mit den Normalenvektoren der Ebenen).


