Komplexere Anwendungsaufgaben mit Extremwertproblemen
Eine rechteckige Blechtafel mit den Seitenlängen und wird zu einem quaderförmigen Gegenstand so geknickt und gebogen, dass dieser an der oberen Mantelfläche halbkreisförmig eingedellt ist. Der Körper sei durch seine beiden Grundflächen abgeschlossen. (Siehe die nachfolgende Skizze.)
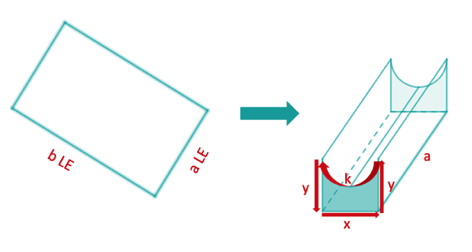
Bestimme das größtmögliche Volumen eines solchen Körpers.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgaben
Für das Volumen des durch Verformen der Blechtafel zu bildenden Körpers gilt nach dem Satz des Cavalieri:
Die Grundfläche und damit auch das Volumen des eingedellten quaderförmigen Körpers hängt von den variablen Größen der Blechtafelseite und dem fest vorgegeben Wert der zweiten Tafelseite ab.
Querschnitt durch den Körper
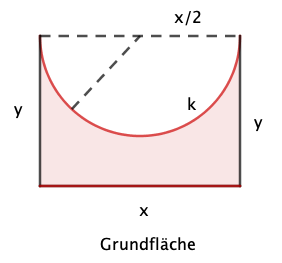
Die Zielfunktion, deren Maximum zu berechnen ist, ergibt sich aus der Differenz der Rechtecksfläche mit den Seitenlängen und und der Fläche des Halbkreises zum Radius , multipliziert mit dem Faktor .
Zielfunktion:
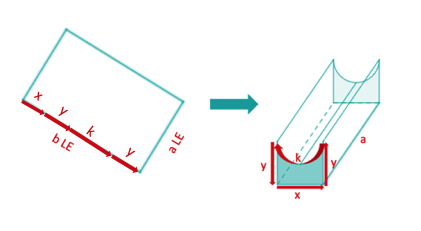
Die zu knickende und umzubiegende Seitenlänge ergibt für die Zielfunktion eine Nebenbedingung.
Nebenbedingung:
Berechne als Kreisbogenlänge des Halbkreises zum Radius .
Setze in die Nebenbedingung ein und löse diese nach (oder auch nach ) auf.
Berechne und .
Setze gleich Null und löse nach auf.
Da für jedes negativ ist, ergibt sich für das Volumen ein Maximum.
Für die maximale Halbkreislinie ergibt dies:
Setze in ein, um die maximale y-Kantenlinie des Körpers zu erhalten:
Setze und in
ein, um das größtmögliche Volumen des Körpers zu erhalten.
Zusammenfassung des Ergebnisses der Teilaufgabe a):
Wird die Blechtafel mit den Seitenlängen und längs der Seite so gebogen, dass die Kantenlängen , , die Halbkreislinie und nochmals die Kante aufeinanderfolgen, so hat der entstehende Körper sein maximales Volumen mit
.
Eine ebene Fläche soll so gebogen werden, dass ein Körper vorgegebener Form entsteht, der ein größtmögliches Volumen besitzt.
Dazu soll dessen Mantelfläche und seine größtmögliche Oberfläche betrachtet werden.
Bestimme seine Mantelfläche.
Die Mantelfläche eines jeden der quaderförmigen eingedellten Körper ist - unabhängig von seinem Volumen - die Fläche der Blechtafel.
Also:
.
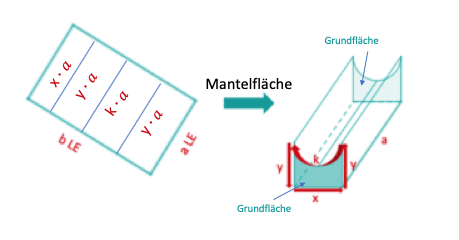
Dies kannst du auch rechnerisch folgendermaßen bestätigen:
Zusammenfassung des Ergebnisses der Teilaufgabe b):
Alle Körper, die sich auf die beschriebene Weise aus der Blechtafel mit den Seitenlängen und herstellen lassen, haben die gleiche Mantelfläche .
Berechne die größtmögliche Oberfläche des Körpers.
Für die Oberfläche eines jeden der betrachteten Körper gilt:
Bereits in Teilaufgabe a) wurde die Grundfläche bestimmt als Differenzfläche eines Rechtecks mit den Seitenlängen und und der Halbkreisfläche zum Radius .
Für die zu maximierende Oberfläche ergibt sich somit die folgende
Zielfunktion:
Ebenso wie für die Volumenoptimierung in Teilaufgabe a) ergibt sich als
Nebenbedingung:
mit .
eingesetzt und nach aufgelöst ergibt:
Setze in ein:
Der Graph von ist wegen des negativen Faktors beim -Glied eine nach unten geöffnete Parabel. Ihr Scheitelpunkt liefert also eine maximale Oberfläche des Körpers.
Mit der 1. Ableitung von bestimmst du den x-Wert der maximalen Oberfläche:
Setze gleich Null um zu bestimmen.
Zusammenfassung des Ergebnisses der Teilaufgabe c):
Die größtmögliche Oberfläche für einen Körper, der in der beschriebenen Weise aus einer Blechtafel mit den Seitenlängen und gebildet werden kann, beträgt
Es ist derselbe Körper, der auch das größtmögliche Volumen aufweist.
Welche Kantenmaße hat dieser größtmögliche Körper für und ?
Der Körper mit dem größten Volumen und gleichzeitig der größten Oberfläche besitzt bei den Blechtafelmaßen und folgende Kantenmaße:
Für das maximale Volumen und die maximale Oberfläche ergibt sich:
Im beigefügten Applet kannst du den Gleitpunkt der Blechtafel verschieben und damit das Verhalten des zu errichtenden Körpers überprüfen und die Ergebnisse für die Blechtafelmaße und überprüfen.
Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unsererDatenschutzerklärung.Anhand des beigefügten Applets kannst du durch Verschieben des rechten unteren Eckpunkts das Verhalten des Körpers und die Ergebnisse für die Blechtafelmaße und überprüfen.
Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unsererDatenschutzerklärung.
