Nachtermin Teil A

Die Skizze unten zeigt das Viereck $A B C D$ mit folgenden Maßen:

$\begin{array}{l} A B = 8,7 cm; C D = 5,2 cm \\ ∢ B A D = ∢ A D C = 90^{\circ}; ∢ D C B = 115^{\circ} \end{array}$

Runden Sie im Folgenden auf eine Stelle nach dem Komma.

Berechnen Sie den Flächeninhalt $A$ des Vierecks $A B C D$ .
$[$ Ergebnis: $A = 52,1 {cm}^{2}$ $]$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus, Kosinus und Tangens
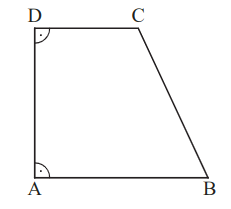
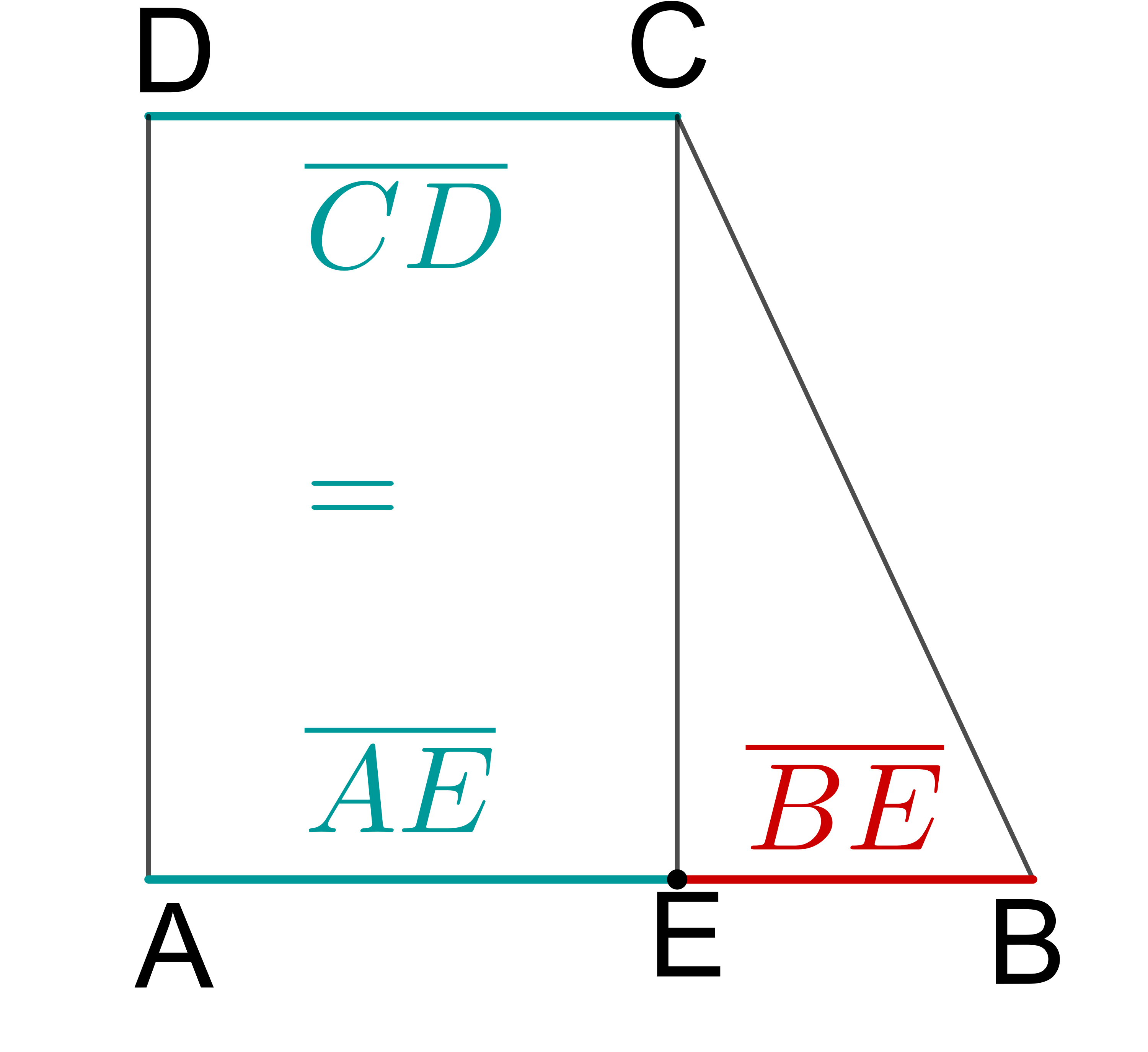
Bei dem Viereck $A B C D$ handelt es sich um ein Trapez. Die Formel für den Flächeninhalt ist also:
$A = A D \cdot \frac{A B + C D}{2}$
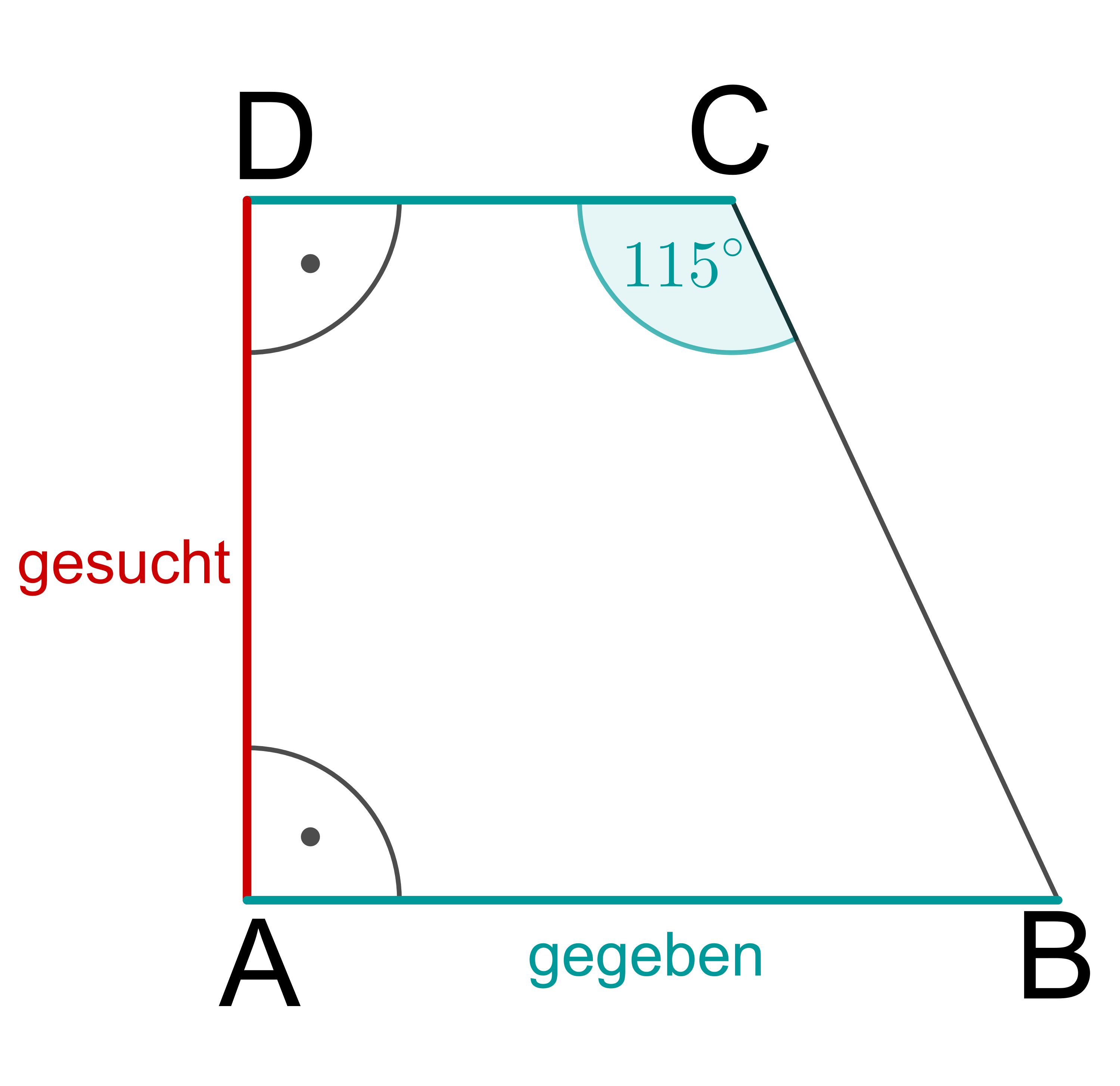
Die Seitenlängen $A B$ und $C D$ sind bereits gegeben, dir fehlt also nur noch die Höhe $A D$ des Trapezes, um dessen Flächeninhalt zu berechnen.
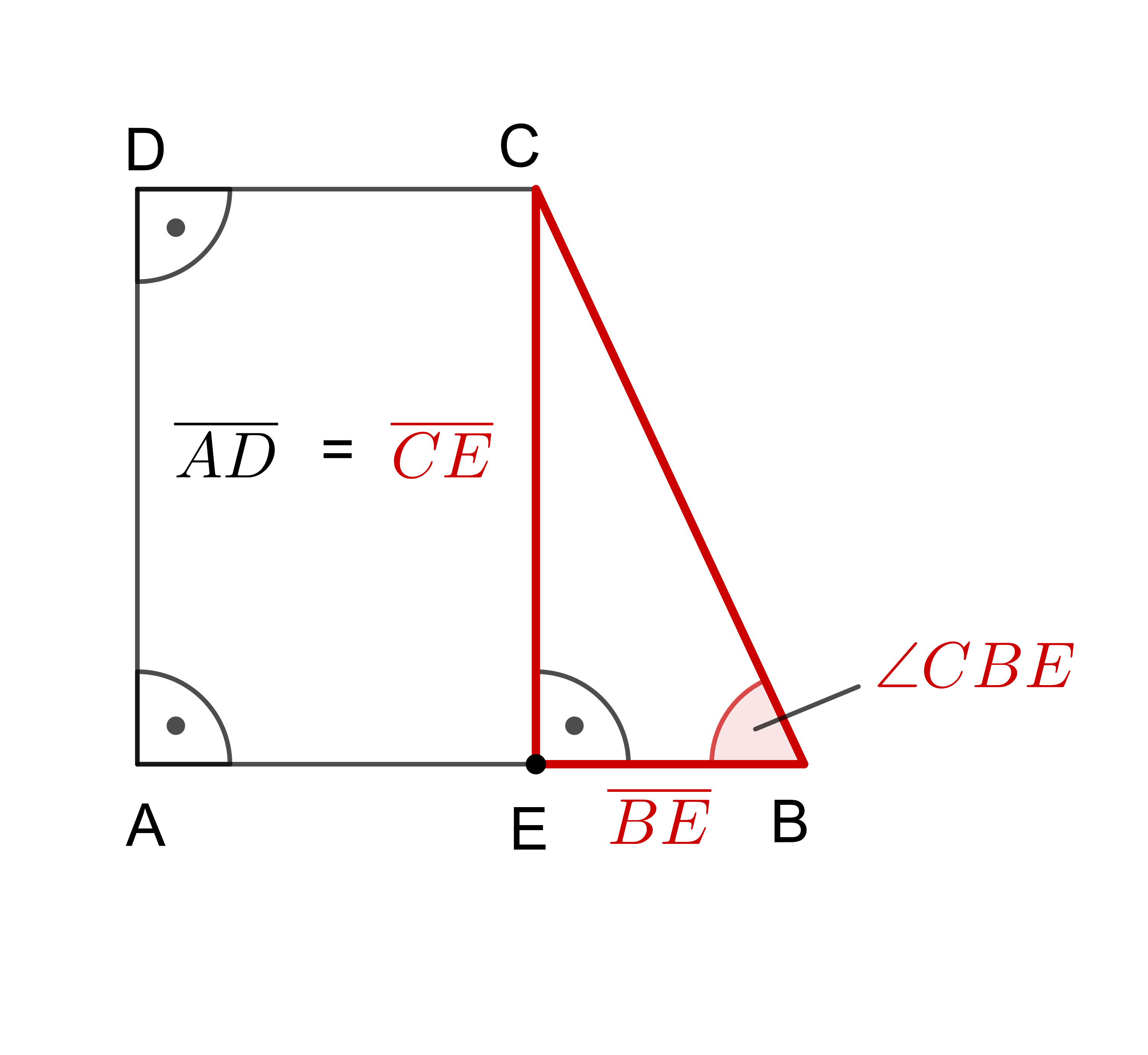
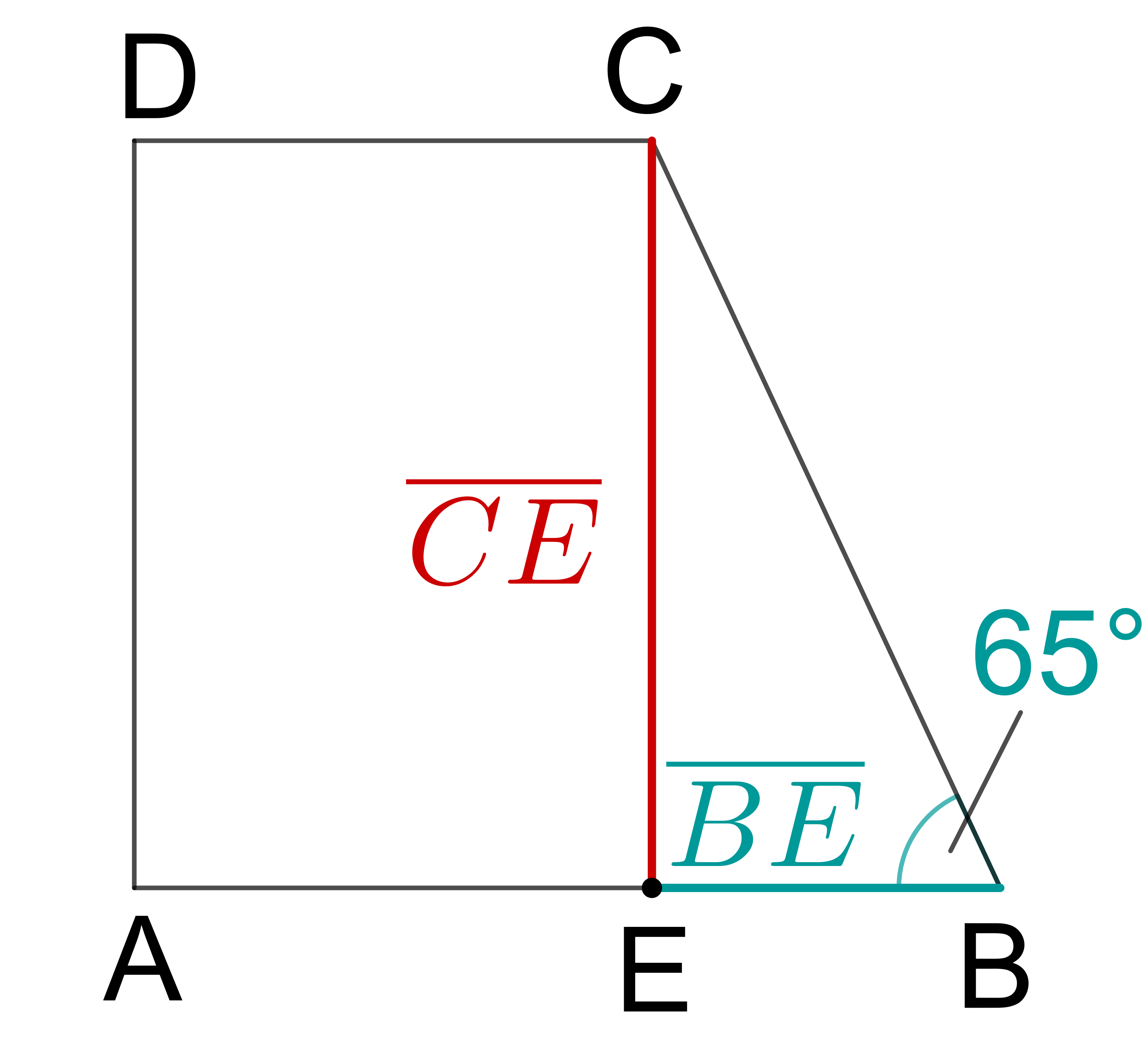
Um auf die Höhe zu kommen, betrachtest du das rechtwinklige Dreieck $E B C$ (im Bild rot Markiert):
Du kannst wie folgt vorgehen:
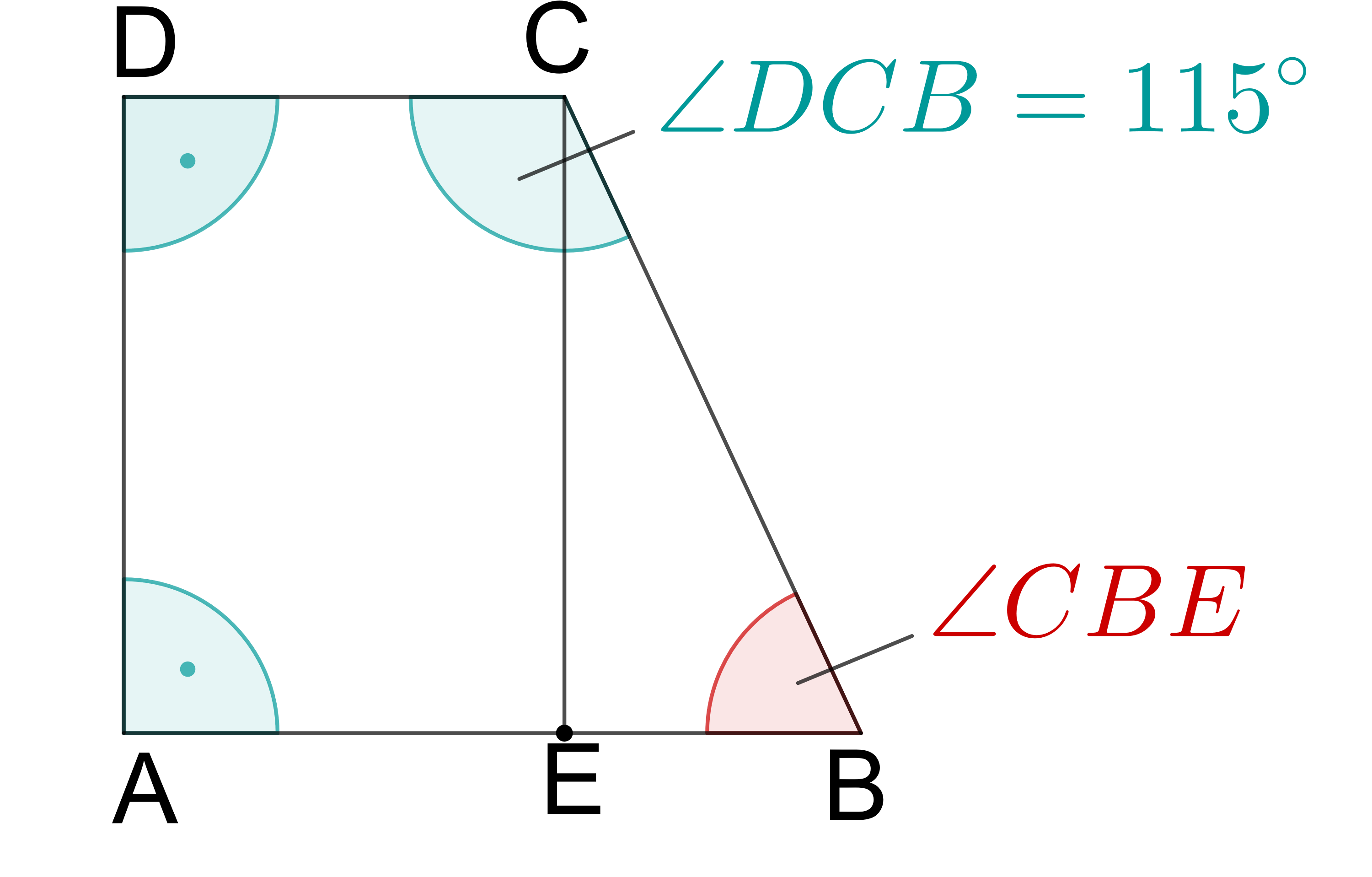
Berechne den Winkel $∢ C B E$ des Dreiecks
Berechne die Seitenlänge $B E$ des Dreiecks.
Berechne mithilfe des Tangens die Höhe $C E$ des Dreiecks.
$C E$ ist genauso lang wie $A D$ . Das ist also die gesuchte Höhe des Trapezes.
1: Berechnung des Winkels $∢ C B E$
Die Innenwinkelsumme eines Trapezes beträgt immer $360 °$ . Da du bereits drei Winkel des Trapezes kennst, kannst du damit den fehlenden Winkel ausrechnen:
$\begin{array}{rcll} 90 ° + 90 ° + 115 ° + ∢ C B E & = & 360 ° \\ 295 ° + ∢ C B E & = & 360 ° & | - 295 ° \\ ∢ C B E & = & 65 ° \end{array}$
2: Berechnung der Seitenlänge $B E$
Gegeben ist die Seitenlänge
$A B = 8,7 cm$ .
Außerdem gilt:
$A E = C D$ .
Die Länge $C D = 5,2 cm$ ist gegeben.
Daher kannst du folgern:
$A E = 5,2 cm$
Und damit kommst du auf die gesuchte Seitenlänge $B E$ :
$\begin{array}{rcl} B E & = & A B - A E \\ = & 8,7 cm - 5,2 cm = 3,5 cm \end{array}$
3: Berechnung der Höhe $C E$
Nun hast du ein rechtwinkliges Dreieck, bei dem du eine Seitenlänge und einen weiteren Winkel kennst. Das reicht aus, um alle anderen Seitenlängen und Winkel auszurechnen. Falls du das noch nicht wusstest, siehe Sinus, Kosinus und Tangens. Das heißt, du kannst nun die Höhe des Dreiecks berechnen:
Du hast in den beiden vorherigen Schritten einen Winkel des Dreiecks ( $∢ C B E = 65 °$ ) und dessen Ankathete ( $B E = 3,5 cm$ ) berechnet. Gesucht ist die Gegenkathete $C E$ dieses Winkels, denn das ist die Höhe des Dreiecks. Also musst du hier den Tangens benutzen:
$\begin{array}{rcl} \tan (65 °) & = & \frac{Gegenkathete}{Ankathete} \\ = & \frac{C E}{B E} \\ = & \frac{C E}{3,5 cm} \end{array}$
Nun multiplizierst du mit $3,5 cm$ :
$\begin{array}{rcl} \tan (65 °) \cdot 3,5 cm & = & C E \\ 7,5 cm & = & C E \end{array}$
Jetzt hast du die Höhe des Trapezes: $A D = C E = 7,5 cm$ .
Du musst das also nur noch in die Formel für den Flächeninhalt einsetzen:
$A = A D \cdot \frac{A B + C D}{2} = 7,5 cm \cdot \frac{8,7 cm + 5,2 cm}{2} = 52,1 {cm}^{2}$
Das Trapez hat also einen Flächeninhalt von $52,1 {cm}^{2}$ .
Hier gehst du zum Beispiel so vor: Überlege dir zuerst, welche Art von Viereck $A B C D$ ist. Wende dann die Formel für den Flächeninhalt dieses Vierecks an und überprüfe, welche Längen du gegeben hast und welche gesucht sind. Berechne dann die fehlenden Längen. Setze zum Schluss alles in die Formel ein.
Der Flächeninhalt des Kreissektors mit dem Mittelpunkt $B$ und dem Mittelpunktswinkel $∢ C B A$ beträgt $5 %$ des Flächeninhalts des Vierecks $A B C D$ . Berechnen Sie den Radius $r$ des Kreissektors.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreissektor
In dieser Aufgabe geht es um einen Kreissektor. Die Formel für den Flächeninhalt ist:
$A_{S e k t o r} = \frac{α}{360} \cdot r^{2} \cdot π$
Dabei ist $A_{S e k t o r}$ der Flächeninhalt des Kreissektors, $α$ der Mittelpunktswinkel und $r$ der Radius. Gesucht ist $r$ . Um $r$ zu ermitteln, berechnest du $A_{S e k t o r}$ und $α$ und stellst dann die Formel nach $r$ um.
Berechnung von $A_{S e k t o r}$
Der Flächeninhalt des Kreissektors beträgt laut Aufgabenstellung $5 %$ von dem Flächeninhalt des Trapezes. Diesen kennst du aus der vorherigen Aufgabe: $A_{T r a p e z} = 52,1 {cm}^{2}$ . Also kannst du nun mit der Formel für die Prozentrechnung $A_{S e k t o r}$ berechnen:
$A_{S e k t o r} = 0,05 \cdot 52,1 {cm}^{2} = 2,6 {cm}^{2}$
Berechnung von $α$
Der Mittelpunktswinkel des Kreissektors ist laut Aufgabenstellung der Winkel $∢ C B A .$ Dieser entspricht dem Winkel $∢ C B E = 65 °$ , den du schon in Aufgabe a) berechnet hast.
Berechnung von r durch Umstellen der Formel
Setzt du nun alles in die Formel für den Flächeninhalt des Kreissektors ein, erhältst du:
$\begin{array}{rcl} A_{S e k t o r} & = & \frac{α}{360^{\circ}} \cdot r^{2} \cdot π \\ 2,6 {cm}^{2} & = & \frac{65^{\circ}}{360^{\circ}} \cdot r^{2} \cdot π \\ r & = & \sqrt{2,6 {cm}^{2} \cdot \frac{1}{π} \cdot \frac{360}{65}} \\ = & 2,1 cm \end{array}$
Also ist der Radius des Kreissektors $2,1 cm .$