Anwendungsaufgaben der Differential- und Integralrechnung
Trassierung
Zwischen zwei Stadtteilen befindet sich in der Nähe des Punktes ein Aussichtsturm.
Von Stadtteil 1 führt eine Stichstraße 1 bis zu diesem Punkt .
Im Stadtteil 2 endet eine Stichstraße 2 im Punkt .
Zur Verbindung der beiden Stadtteile soll eine Straße von nach gebaut werden.
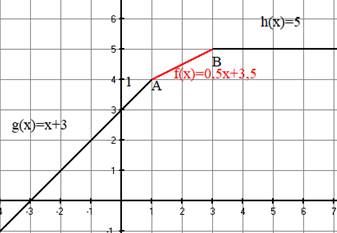
Die Straße 1 ist für gegeben durch: .
Die Straße 2 ist für gegeben durch: .
Gesucht ist eine lineare Funktion , die den Straßenverlauf zwischen den Punkten und beschreibt. An den Anschlussstellen soll kein „Versatz“ auftreten.
Zeichne die Funktionen und die berechnete Funktion in ein Koordinatensystem ein.
Beschreibe den Straßenverlauf an den beiden Übergangsstellen und .
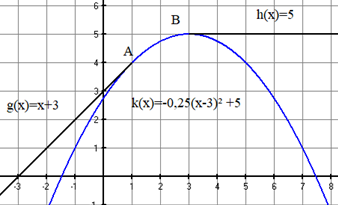
Gesucht ist nun eine quadratische Funktion zur Verbindung der beiden Stichstraßen. Die Anschlussstellen sollen "versatzfrei" sein und keinen „Knick“ aufweisen sein.
Die Straßenbauingenieure sind immer noch nicht zufrieden. Sie stellen an den beiden Anschlussstellen fest, dass sich die Krümmung der Funktion an der Stelle von der Krümmung der Funktion unterscheidet bzw. an der Stelle von der Krümmung der Funktion unterscheidet.
Dadurch kommt es an den Übergangsstellen zu einem sogenannten „Krümmungsruck“.
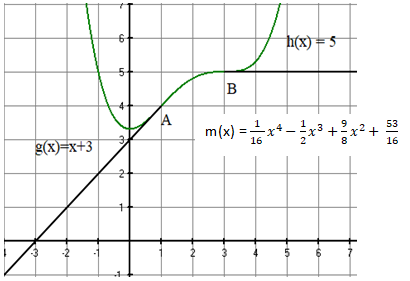
Gesucht ist nun eine Funktion 4. Grades zur Verbindung der beiden Stichstraßen. Die Anschlussstellen sollen "versatzfrei" sein, keinen „Knick“ aufweisen und "krümmungsruckfrei"sein.
Hinweis: Ein „krümmungsruckfreier“ Übergang an einer Stelle bzw. ist möglich, wenn die Bedingungen bzw.
erfüllt sind.