Analysis, Teil A, Aufgabengruppe 1

Eine Funktion f ist durch $f (x) = 2 \cdot e^{\frac{1}{2} x} - 1$ mit $x \in ℝ$ gegeben.

Ermitteln Sie die Nullstelle der Funktion $f$ . (2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen berechnen
Um die Nullstelle zu bestimmen, ermittelt man, wann der Funktionswert $f (x)$ gleich $0$ ist.
$f (x)$ $=$ $0$
$2 e^{\frac{1}{2} x} - 1$ $=$ $0 | + 1$
$2 e^{\frac{1}{2} x}$ $=$ $1 | : 2$
$e^{\frac{1}{2} x}$ $=$ $\frac{1}{2}$
Verwende hier am besten den natürlichen Logarithmus, um die Exponentialgleichung aufzulösen.
$\frac{1}{2} x$ $=$ $\ln (\frac{1}{2})$
Du kannst noch den Logarithmus mit Hilfe der Logarithmusrechenregeln umschreiben (musst du aber nicht unbedingt).
$\frac{1}{2} x$ $=$ $\ln (1) - \ln (2)$
$\frac{1}{2} x$ $=$ $0 - \ln (2)$
$x$ $=$ $- \ln (2)$ $\cdot 2$
$x$ $=$ $- 2 \ln (2)$
Die Nullstelle ist bei $x = - 2 l n (2)$ .
Die Tangente an den Graphen von $f$ im Punkt $S (0 | 1)$ begrenzt mit den beiden Koordinatenachsen ein Dreieck. Weisen Sie nach, dass dieses Dreieck gleichschenklig ist. (3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichschenkliges Dreieck
Ein gleichschenkliges Dreieck ist durch zwei gleich lange Seiten gekennzeichnet. Also musst du etwas über die Seitenlängen herausfinden, wofür du die Tangentengleichung brauchst.
Dementsprechend ist der erste Schritt, die Tangentengleichung im Punkt $S (0 | 1)$ aufzustellen. Danach berechnest du den Schnittpunkt mit der $x$ -Achse und zuletzt ermittelst du die Seitenlängen.
Tangentengleichung aufstellen
Dazu berechnest du zuerst die Steigung in diesem Punkt. Für die Steigung bildest du die Ableitung. Hier musst du die Verkettung der Funktion beachten.
$f^{'} (x)$ $=$ $2 \cdot e^{\frac{1}{2} x} \cdot \frac{1}{2} = e^{\frac{1}{2} x}$
Anschließend setzt du den $x$ -Wert des Schnittpunktes ein.
$f^{'} (0)$ $=$ $e^{\frac{1}{2} \cdot 0} = e^{0} = 1$
Die Tangentensteigung beträgt also $1$ . Das kannst du in die allgemeine Tangentengleichung $y = m x + t$ einsetzen: $y = 1 \cdot x + t = x + t$ .
Um den verbleibenden Parameter $t$ zu bestimmen, setzt du die Koordinaten des Punktes ein:
$1$ $=$ $0 + t = t$
Also ist $t = 1$ und die Tangente hat die Form $y = x + 1$ .
Schnittpunkte mit den Koordinatenachsen
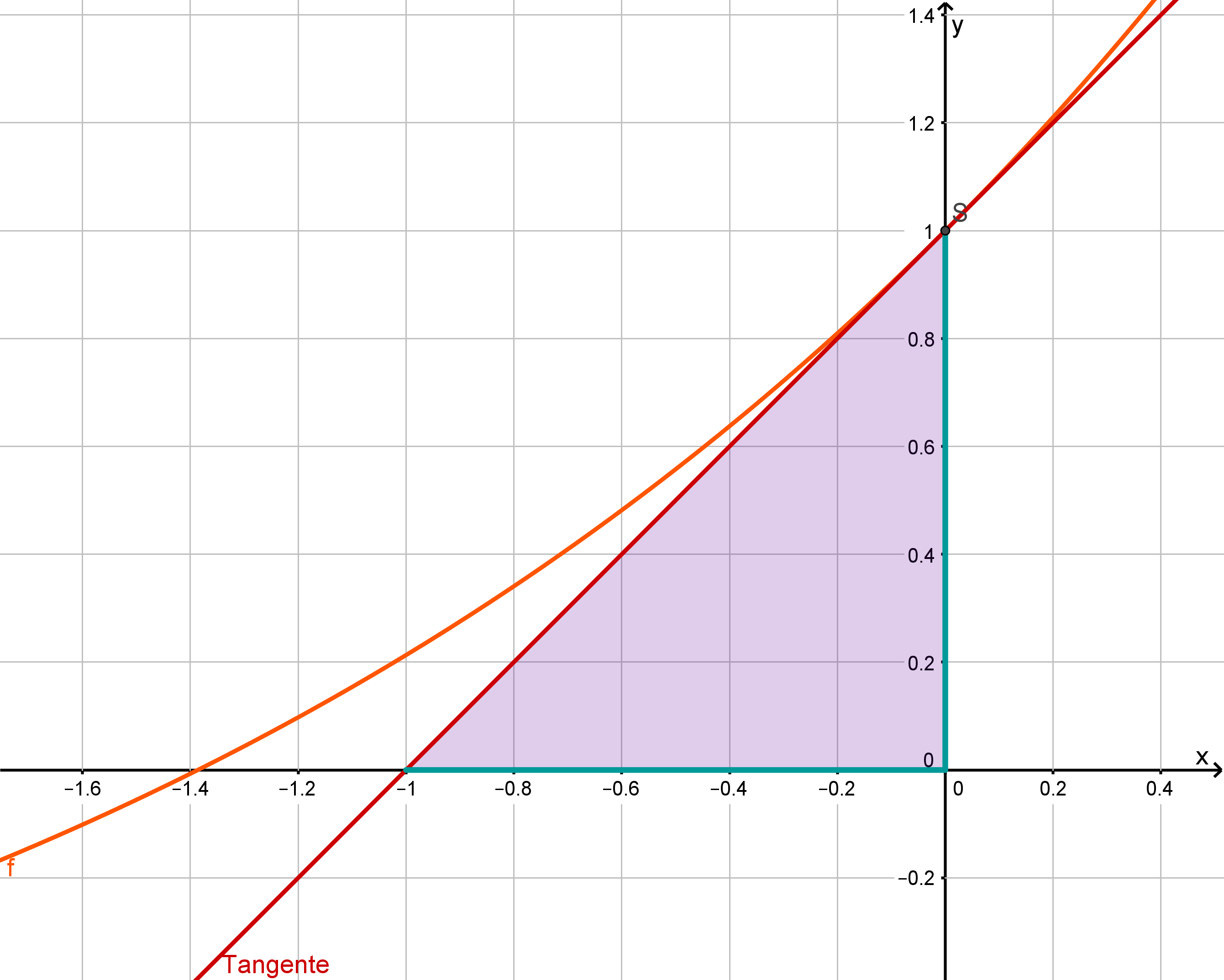
Für das Dreieck sind die Schnittpunkte mit den Koordinatenachsen wichtig. Der Schnittpunkt mit der $y$ -Achse ist der gegebene Punkt $S (0 | 1)$ . Der Schnittpunkt mit der $x$ -Achse muss ausgerechnet werden:
$0$ $=$ $x + t$
$x$ $=$ $- t$
Der Schnittpunkt mit der $x$ -Achse liegt also bei $(- 1 | 0)$ .
Längen ablesen
Du stellst fest, dass die Schnittpunkte der beiden Seiten, die auf den Koordinatenachsen liegen, jeweils den Abstand $1$ vom Ursprung haben. Damit haben sie beide die Länge $1$ und vor allem die gleiche Länge, weswegen das Dreieck gleichschenklig ist.

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das? serlo.org

$f (x)$	$=$	$0$
$2 e^{\frac{1}{2} x} - 1$	$=$	$0 \| + 1$
$2 e^{\frac{1}{2} x}$	$=$	$1 \| : 2$
$e^{\frac{1}{2} x}$	$=$	$\frac{1}{2}$

$\frac{1}{2} x$	$=$	$\ln (1) - \ln (2)$
$\frac{1}{2} x$	$=$	$0 - \ln (2)$
$x$	$=$	$- \ln (2)$	$\cdot 2$
$x$	$=$	$- 2 \ln (2)$

Analysis, Teil A, Aufgabengruppe 1

Tangentengleichung aufstellen

Schnittpunkte mit den Koordinatenachsen

Längen ablesen