Komplexere Anwendungsaufgaben mit Extremwertproblemen

Da die rechteckige Blechtafel V-förmig geknickt wird, entsteht aus dem ebenen Rechteck ein gerades dreiseitiges Prisma mit der Höhe $a$.

Für das Volumen der geknickten Dachrinne gilt somit:

$V_{\text{Dachrinne}}={\text{Dreiecksfläche}}_{△ABC}\cdot a$

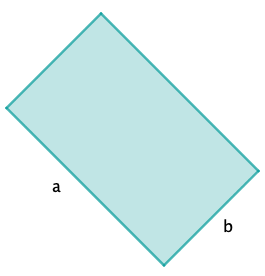
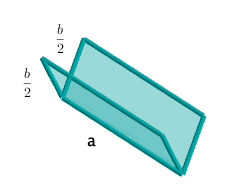
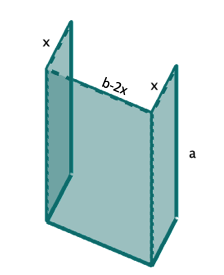
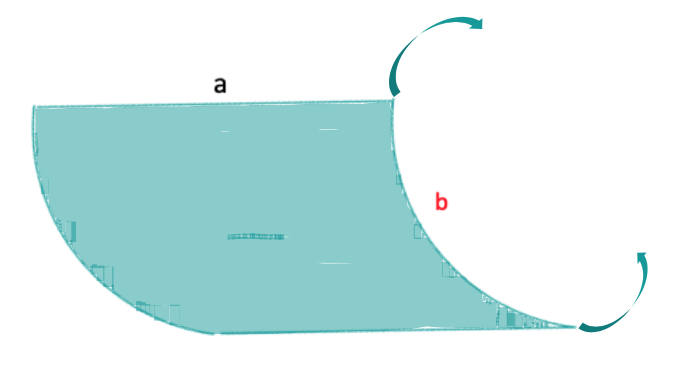
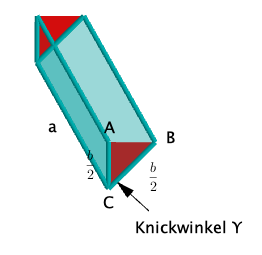
Und da der Buchstabe V achsensymmmetrisch ist, ist die Grundfläche des Prismas ein gleichschenkliges Dreieck mit der vorgegebenen Schenkellänge $${\displaystyle \frac{b}{2}}$$, dessen Flächeninhalt A vom Knickwinkel $\gamma$ abhängt.

$\gamma$ ist ein Winkel zwischen $0°$ und $180°$.

Die Abhängigkeit der Dreiecksfläche $A_{△ABC}$ von $\gamma$ kannst du an dem gegebenen Applet für $b=4LE$ nachvollziehen.

Wegen des fest vorgegebenen Wertes $a$ für die Höhe des Prismas ist sein Volumen dann am größten, wenn die Dreiecksfläche $A_{△ABC}$ maximal ist.

Als Zielfunktion für die Extremwertaufgabe, das größtmögliche Dachrinnenvolumen zu ermitteln, verwendest du im weiteren deshalb die von $\gamma$ abhängige Dreiecksfläche.

Das Applet macht deutlich, dass sowohl die Grundlinie wie auch die Höhe des Dreiecks vom Knickwinkel $\gamma$ abhängen und mit diesem variieren.

Für die Dreiecksfläche der Grundfläche des Prismas gilt:

$A_{△ABC}=\frac{1}{2}\cdot \text{Grundlinie}\cdot \text{Höhe}$

Also ergibt sich die

Zielfunktion

$A(c;h)=c\cdot h$

mit $c\in [0;b/2]$ und $h\in [0;b/2]$

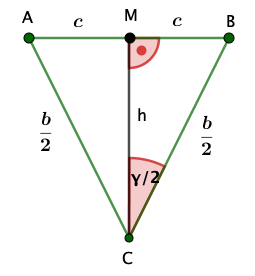
Das gleichschenklige Dreieck $ABC$ enthält das rechtwinklige Teildreieck $BMC$ mit der gegebenen Hypotenusenlänge $b/2$ und dem variierenden Winkel $\gamma /2$.

Mit Hilfe der trigonometrischen Funktionen $Sinus$ und $Cosinus$ kannst du nun die Dreiecksfläche als Funktion des Knickwinkels $\gamma$ darstellen.

1. Nebenbedingung

$${\displaystyle sin\frac{\gamma }{2}=\frac{c}{\frac{b}{2}}}$$

2. Nebenbedingung

$${\displaystyle cos\frac{\gamma }{2}=\frac{h}{\frac{b}{2}}}$$

Löse die 1. Nebenbedingung nach $c$ und die 2. Nebenbedingung nach $h$ auf.

$${\displaystyle c=\frac{b}{2}\cdot sin\frac{\gamma }{2}}$$

$${\displaystyle h=\frac{b}{2}\cdot cos\frac{\gamma }{2}}$$

Setze $c$ und $h$ in $A(c;h)$ ein, um die Dreiecksfläche als Funktion von $\gamma$ zu erhalten.

Erinnerung: $b$ ist ein konstanter Wert.

Zielfunktion

$${\displaystyle A(\gamma )=(\frac{b}{2}\cdot sin\frac{\gamma }{2})\cdot (\frac{b}{2}\cdot cos\frac{\gamma }{2})}$$

Fasse zusammen.

$${\displaystyle A(\gamma )=\frac{b^2}{4}\cdot sin\frac{\gamma }{2}\cdot cos\frac{\gamma }{2}}$$

Bilde unter Verwendung der Produktregel und der Kettenregel die Ableitung $A^{\prime }(\gamma )$.

$A^{\prime }(\gamma )=\frac{b^2}{4}\cdot (\underset{\text{Produktregel}}{\underbrace{\underset{\text{Kettenregel}}{\underbrace{\frac{1}{2}cos\frac{\gamma }{2}}}-\underset{\text{Kettenregel}}{\underbrace{\frac{1}{2}sin\frac{\gamma }{2}}}}})|\frac{1}{2}\text{ausklammern}$

$${\displaystyle A^{\prime }(\gamma )=\frac{b^2}{8}\cdot (cos\frac{\gamma }{2}-sin\frac{\gamma }{2})}$$

Setze $A^{\prime }(\frac{\gamma }{2})$ gleich Null um zu berechnen, für welchen Knickwinkel $\gamma$ die Grundfläche des Dachrinnenprimas maximal sein kann.

$$\begin{array}{rcll}{\displaystyle \frac{b^2}{8}\cdot (cos\frac{\gamma }{2}-sin\frac{\gamma }{2})}& =& 0& |:{\displaystyle \frac{b^2}{8}}\\ {\displaystyle cos\frac{\gamma }{2}-sin\frac{\gamma }{2}}& =& 0& |{\displaystyle +sin\frac{\gamma }{2}}\\ {\displaystyle cos\frac{\gamma }{2}}& =& {\displaystyle sin\frac{\gamma }{2}}& |{\displaystyle :cos\frac{\gamma }{2}}\\ 1& =& {\displaystyle tan\frac{\gamma }{2}}& |ta{n}^{-1}\\ {\displaystyle \frac{\gamma }{2}}& =& 45°& |\cdot 2\\ \gamma & =& 90°& \end{array}$$

Um nachzuweisen, dass $A(\gamma )$ für $\gamma =90°$ tatsächlich maximal ist, hast du zwei Möglichkeiten.

Möglichkeit 1

Bilde die 2. Ableitung von $A(\gamma )$.

$${\displaystyle A^{\prime }(\gamma )=\frac{b^2}{8}\cdot (cos\frac{\gamma }{2}-sin\frac{\gamma }{2})\Rightarrow }$$

$${\displaystyle A^{\prime \prime }(\gamma )=\frac{b^2}{8}\cdot (\underset{\text{Kettenregel}}{\underbrace{-\frac{1}{2}sin\frac{\gamma }{2}}}-\underset{\text{Kettenregel}}{\underbrace{\frac{1}{2}cos\frac{\gamma }{2}}})}$$

$-\frac{1}{2}$ ausklammern

$${\displaystyle A^{\prime \prime }(\gamma )=-\frac{b^2}{16}\cdot (sin\frac{\gamma }{2}+cos\frac{\gamma }{2})}$$

Setze $\gamma =90°$ ein:

$${\displaystyle A^{\prime \prime }(90°)=-\frac{b^2}{16}\cdot (\frac{1}{2}\sqrt{2}+\frac{1}{2}\sqrt{2})<0\Rightarrow }$$

$\text{}\gamma =90°$ liefert maximalen Flächeninhalt des Grunddreiecks.

Möglichkeit 2 ohne Benutzung der 2. Ableitung:

Die Funktion $A(\gamma )$ hat für die Randpunkte des Definitionsbereichs ($\gamma =0°$ und $\gamma =180°$) ihr Minimum $0$. Dann liefert das (einzige) lokale Extremum dazwischen ein Maximum.

$A(0°)=0$ und $A(180°)=0\Rightarrow A(90°)\text{liefert ein Maximum.}$

Für das Volumen der v-förmig geknickten Dachrinne galt:

$V_{\text{Dachrinne}}=\text{Dreiecksfläche}\cdot a$.

Somit ergibt sich für das größtmöglichde Volumen dieser Dachrinne:

$${\displaystyle V_{max}=\frac{b^2}{4}\cdot sin(45°)\cdot cos(45°)\cdot a}$$.

Also:

$${\displaystyle V_{max}=\frac{1}{8}a{b}^2}$$

Da die Blechtafel rechtwinklig geknickt wird, entsteht aus dem ebenen Rechteck ein Quader mit der Höhe a und einem Rechteck mit den Seitenlängen $x$ und $y$ als Grundfläche.

Für das Volumen des Quaders gilt somit:

$V_{\text{Quader}}=\text{Grundfläche}\cdot a$

Da das Volumen des Quaders maximal werden soll, erhältst du folgende

Zielfunktion

mit $${\displaystyle x\in ]0;\frac{b}{2}[}$$ und $y\in ]0;b[$ und der Konstanten $a$.

Da die Blechtafel achsensymmetrisch zur Seite $b$ geknickt wird ergibt sich als

Nebenbedingung

$\text{}\begin{array}{rl}2x+y& =b\\ y& =b-2x\end{array}$

Setze y in $V(x;y)$ ein.

$V(x)=x\cdot (b-2x)\cdot a$

$V(x)=(-2x^2+bx)\cdot a$

Bilde $V^{\prime }(x)$.

$V^{\prime }(x)=(-4x+b)\cdot a$

Setze $V^{\prime }(x)$ gleich Null und löse nach $X$ auf.

$$\begin{array}{rcll}(-4x+b)\cdot a& =& 0& |:a\\ -4x+b& =& 0& \\ x& =& {\displaystyle \frac{b}{4}}& \end{array}$$

Argumentiere, dass sich für $x=b/4$ ein Maximum ergibt.

Es gilt:

$A^{\prime \prime }(\gamma )=-4a<0$.

$A^{\prime \prime }(x)$ ist also eine negative Konstante.

Das Extremum ist also ein Maximum.

Ohne Benutzung der 2. Ableitung kannst du auch so argumentieren:

Der Graph der Funktion $A(\gamma )$ ist eine nach unten geöffnete Parabel. Das lokale Extremum deshalb ein Maximum.

$x=\frac{b}{4}$ in $V(x)=(-2x^2+bx)\cdot a$ eingesetzt, ergibt das größtmögliche Volumen $V_{max}$ dieser Dachrinne:

$${\displaystyle V_{max}=(-2\cdot \frac{b^2}{16}+b\cdot \frac{b}{4})\cdot a}$$

Also:

$${\displaystyle V_{max}=\frac{a{b}^2}{8}}$$

Diese Teilaufgabe ist keine Extremwertaufgabe. Das halbkreisförmig gebogene Blechrechteck ergibt eine Zylinderhälfte der Höhe $a$. Dessen Volumen ist mit den Ergebnissen der Teilaufgaben a) und b) zu vergleichen.

Der Umfang des (ganzen) Grundkreises ist $2b$.

Dann gilt für den Radius $r$:

$$2r\pi =2b\Rightarrow r={\displaystyle \frac{b}{\pi }}$$

Die Dachrinne, d.h. der halbe Zylinder, hat dann folgendes Volumen:

$$V_{Rinne}={\displaystyle \frac{1}{2}\cdot {\left(\frac{b}{\pi }\right)}^2\cdot \pi \cdot a}$$.

Damit ergibt sich:

$$V_{Rinne}={\displaystyle \frac{1}{2\pi }\cdot a\cdot b^2\approx \mathrm{0,16}a{b}^2}$$

Der Vergleich der drei Teilaufgaben ergibt:

Die beiden maximalen Dachrinnenvolumina der Teilaufgaben a) und b) sind mit $\mathrm{0,125}a{b}^2$ gleich und kleiner als das halbkreisförmig gebogene Volumen der Teilaufgabe c) mit $\mathrm{0,16}a{b}^2$. Dieses ist somit um rund $28\%$ größer als das Maximum jeder geknickten Rinne.