Analysis, Teil B, Aufgabengruppe 2

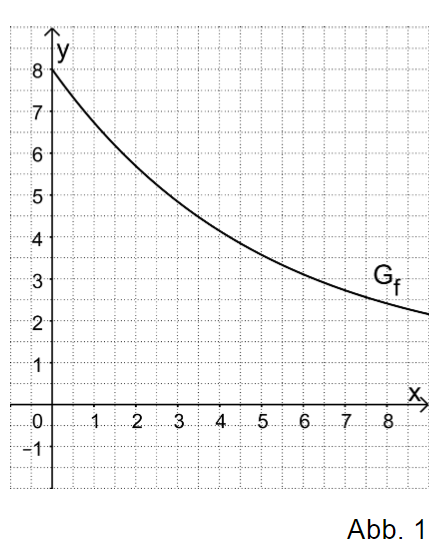
Gegeben ist die Funktion $f : x \mapsto 1 + 7 e^{- 0,2 x}$ mit Definitionsbereich $ℝ_{0}^{+}$ ; die Abbildung 1 zeigt ihren Graphen $G_{f}$ .

a) Begründen Sie, dass die Gerade mit der Gleichung $y = 1$ waagrechte Asymptote von $G_{f}$ ist. Zeigen Sie rechnerisch, dass $f$ streng monoton abnehmend ist.

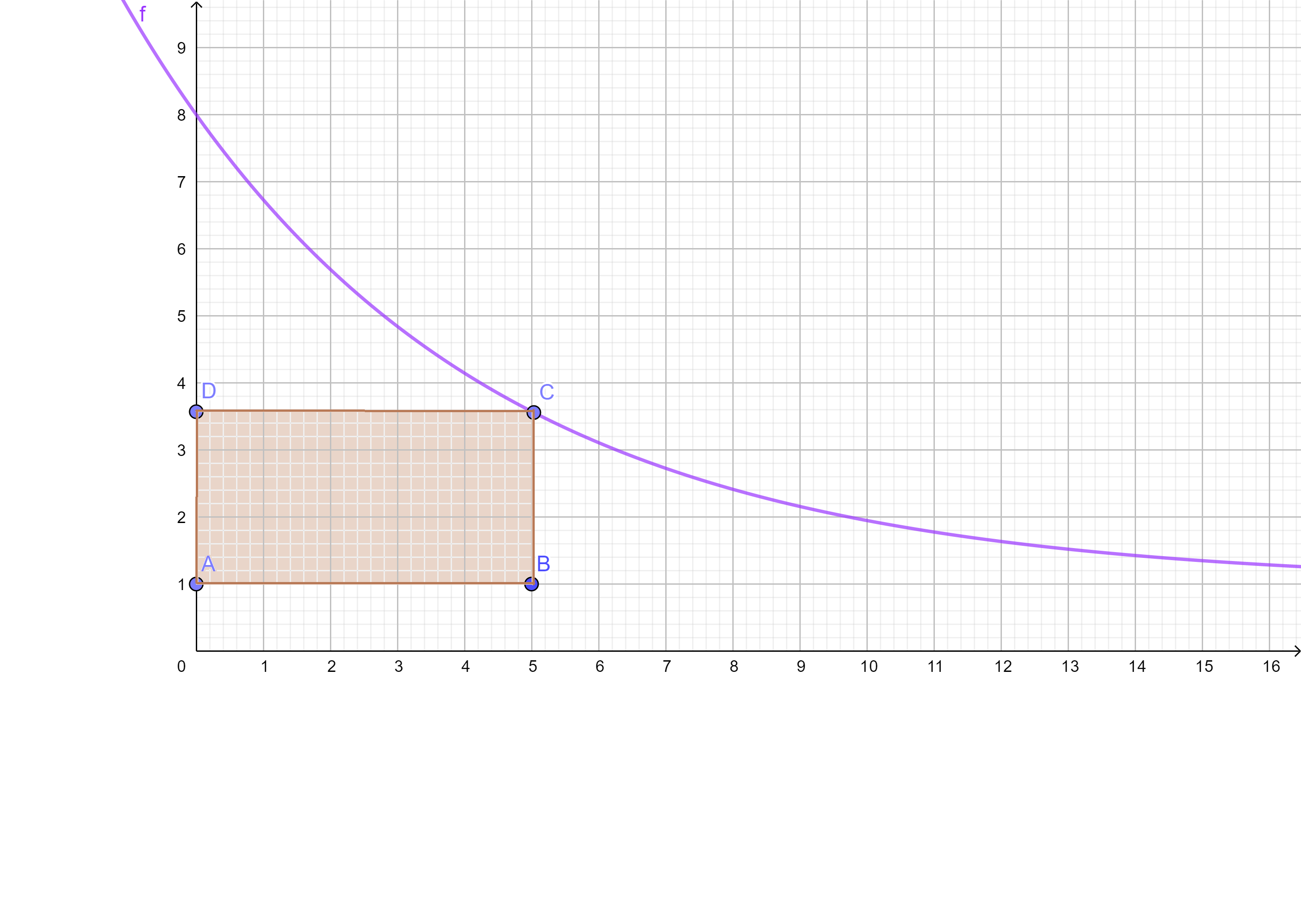
Für jeden Wert $s > 0$ legen die Punkte $(0 | 1)$ , $(s | 1)$ , $(s | f (s))$ und $(0 | f (s))$ ein Rechteck mit dem Flächeninhalt $R (s)$ fest.

b) Zeichnen Sie dieses Rechteck für $s = 5$ in die Abbildung 1 ein. Zeigen Sie, dass $R (s)$ für einen bestimmten Wert von $s$ maximal ist, und geben Sie den Wert von $s$ an.

(zur Kontrolle: $R (s) = 7 s \cdot e^{- 0,2 s}$ )

c) Berechnen Sie den Inhalt des Flächenstücks, das von $G_{f}$ , der y-Achse sowie den Geraden mit den Gleichungen $y = 1$ und $x = 5$ begrenzt wird. Einen Teil dieses Flächenstücks nimmt das zu $s = 5$ gehörige Rechteck ein. Bestimmen Sie den prozentualen Anteil des Flächeninhalts dieses Rechtecks am Inhalt des Flächenstücks.

Teilaufgabe a)

Die e-Funktion $e_{1} (x) = e^{x}$ hat die x-Achse als waagrechte Asymptote. Da $e_{2} (x) = e^{- x}$ sich aus $e_{1} (x)$ durch Spiegelung an der y-Achse ergibt, ist die x-Achse ebenfalls eine waagrechte Asymptote von $e_{2} (x)$ .

Der Graph $G_{e_{2}}$ ergibt sich aus dem Graph $G_{e_{1}}$ durch Spiegelung an der y-Achse.

Also gilt: $\lim_{x \to \infty} e^{- x}$ =0 und $\lim_{x \to \infty} (1 + 7 \cdot e^{- 0,2 \cdot x}) = 1$

Die Funktion $f$ ist streng monoton fallend, wenn $f^{'} (x) < 0$ für alle $x > 0$

f^{'} (x) = 7 \cdot (- 0,2) \cdot e^{- 0,2 \cdot x} = - 1,4 \cdot e^{- 0,2 \cdot x} < 0

Da $e^{- 0,2 \cdot x} > 0$ , ist also $- 1,4 \cdot e^{- 0,2 \cdot x} < 0$ . Somit ist $f$ streng monoton fallend.

Teilaufgabe b)

Bei dieser Aufgabe gehst du in zwei Schritten vor:

Zuerst berechnest du die Fläche des Rechtecks R(s) in Abhängigkeit von $s$ .
Dann berechnest du mithilfe der ersten Ableitung, wann R(s) maximal wird.

Das Rechteck mit den gegebenen Punkten hat die Länge $s$ und die Höhe

h = f (s) - 1 = 7 \cdot e^{- 0,2 \cdot s} .

Damit gilt für den Flächeninhalt:

R (s) = s \cdot 7 \cdot e^{- 0,2 \cdot s} = 7 \cdot s \cdot e^{- 0,2 \cdot s} .

Dieser Wert wird maximal für den Wert von $s$ , wenn $R^{'} (s) = 0$ und an der Stelle $s$ einen Vorzeichenwechsel von $+$ nach $-$ hat.

R^{'} (s) = 7 \cdot [e^{- 0,2 \cdot s} + s \cdot (e^{- 0,2 \cdot s} \cdot (- 0,2))] = 7 \cdot e^{- 0,2 \cdot s} \cdot (1 - 0,2 \cdot s)

Berechne nun die Nullstelle von R(s):

$R^{'} (s)$	$=$	$0$
	↓	Setze R'(s) ein
$1 - 0,2 \cdot s$	$=$	$0$	$- 1$
$- 0,2 \cdot s$	$=$	$- 1$	$\cdot (- 5)$
$s$	$=$	$5$

Da der Faktor $7 \cdot e^{- 0,2 \cdot s}$ immer größer als 0 ist, wird das Vorzeichen von $R^{'} (s)$ bestimmt von dem zweiten Faktor $1 - \frac{1}{5} \cdot s$

Der zweite Faktor ist eine fallende Gerade mit dem y-Achsenabschnitt 1 und der Nullstelle $s = 5$ .

Also ist $R^{'} (s) > 0$ für $0 < s < 5$ : $R$ wachsend.

Und $R^{'} (s) < 0$ für $5 < s < \infty$ : $R$ fallend.

Damit wird der Inhalt des Rechteckes für $s = 5$ maximal. Es gilt:

R (5) = 5 \cdot 7 \cdot e^{- 0,2 \cdot 5} = 35 \cdot e^{- \frac{1}{5} \cdot 5} = 35 \cdot e^{- 1} = \frac{35}{e} FE

Teilaufgabe c)

Für den Inhalt des vor beschriebenen Flächenstücks gilt:

$A$	$=$	$\int_{0}^{5} (f (x) - 1) d x$
	↓	Setze f(x) ein
	$=$	$\int_{0}^{5} (1 + 7 \cdot e^{- 0,2 x} - 1) d x$
	↓	Vereinfache
	$=$	$\int_{0}^{5} 7 \cdot e^{- 0,2 x} d x$
	↓	Ziehe die 7 als Skalar vor das Integral
	$=$	$7 \int_{0}^{5} e^{- \frac{1}{5} x} d x$
	↓	Integriere
	$=$	$7 \cdot (- 5) [e^{- \frac{1}{5} x}]_{0}^{5}$
	↓	Werte an den Grenzen aus
	$=$	$- 35 \cdot (e^{- 1} - e^{0}) = 35 - \frac{35}{e} FE$

Damit gilt für den Anteil des Flächenstücks des Rechtecks am Inhalt des Flächenstücks:

\frac{R (5)}{A} = \frac{\frac{35}{e}}{35 - \frac{35}{e}} = \frac{\frac{35}{e}}{\frac{35 e - 35}{e}} = \frac{35}{35 e - 35} = \frac{35}{35} \cdot \frac{1}{e - 1} = \frac{1}{e - 1} = 0,58

Also ist der prozentuale Anteil gerade 58 %.

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das? serlo.org