Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
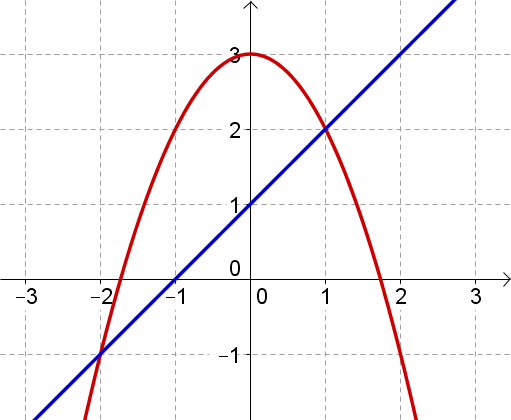
Schraffiere diese Fläche
Funktionsterme von f und g
Berechnung des zur Parabel gehörenden Funktionsterms:
Der Scheitel der Parabel kann abgelesen werden:
Benutze die Scheitelpunktsform:
Weiterhin kann der Punkt abgelesen werden.
Setze den Punkt in ein:
| | | |
| ↓ | Löse nach auf. |
| | | |
| | | |
Die Parabel hat die Funktionsgleichung
Die Geradengleichung kann direkt abgelesen werden:
(Steigung und der y-Achsenabschnitt ):
Berechnung der beiden Schnittpunkte und der Graphen
| | | |
| ↓ | Bringe alle Terme auf eine Seite. |
| | | |
| | | |
| | | |
| ↓ | Setze und ein. |
| | | |
| | | |
| | | |
Damit ist und
Setze beide Werte z.B. in ein, um die Funktionswerte der beiden Schnittpunkte zu erhalten:
Die beiden Schnittpunkte und der Graphen sind und .
Gib A als bestimmtes Integral an
| | | |
| ↓ | Setze und ein. |
| | | |
| ↓ | Löse die Klammer auf und fasse zusammen. |
| | | |
| | | |
| | | |
| ↓ | Löse die Klammern auf |
| | | |
| ↓ | Fasse zusammen. |
| | | |
| | | |
| | | |
Die beiden Graphen schließen eine Fläche mit dem Inhalt ein.