Lösung Teilaufgabe a)
Durchführung
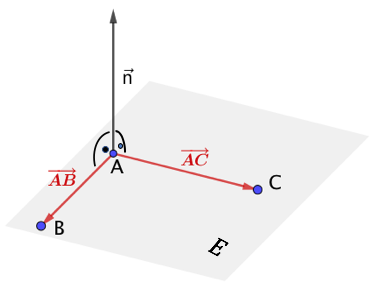
Die Punkte , , ergeben:
Der Vektor ist also ein Normalenvektor der Ebene .
Anmerkung:
Das Vorziehen des Faktors hat lediglich den "Schönheitsaspekt", dass der ab jetzt verwendete Normalenvektor nur ein Minuszeichen besitzt. Jedes Vielfache eines Normalenvektors steht auch auf der Ebene senkrecht und ist somit ebenfalls ein Normalenvektor.
3.Aufstellen der Ebenengleichung
Die Aufgabenstellung lässt dir die Wahl, ob du die gesuchte Normalenform der Ebenengleichung in Vektorform oder in Koordinatendarstellung angeben willst.
a) Vektorform mit Aufpunkt
Setze gleich Null.
Setze für den Punkt seinen Ortsvektor und die Vektorkoordinaten von ein.
Dies ist die gesuchte Ebene. Du kannst sie durch Ausmultiplizieren des Skalarproduktes auch noch in die Koordinatendarstellung bringen.
b) Ansatz für in Koordinatendarstellung
Mit dem Normalenvektor und einem beliebigen Punkt der Ebene, z.B. (es muss nicht wieder der Punkt sein) kannst du so ansetzen:
Setze den Punkt ein und löse nach auf.
Also:
Lösung Teilaufgabe b)
Ein beliebiger Punkt der -Achse hat die Koordinaten .
Setze in die Normalengleichung von ein und berechne .
Die Ebene schneidet die -Achse im Punkt .