Geometrie, Teil A, Aufgabengruppe 1

Für jeden Wert von $a$ mit $a \in ℝ$ ist eine Gerade $g_{a}$ gegeben durch

$g_{a} : \vec{X} = (\begin{array}{c} 2 \\ a - 4 \\ 4 \end{array}) + λ \cdot (\begin{array}{c} 2 \\ - 2 \\ 1 \end{array}), λ \in ℝ$ .

(2 BE)

Bestimmen Sie in Abhängigkeit von $a$ die Koordinaten des Punktes, in dem $g_{a}$ die $x_{1} x_{2}$ -Ebene schneidet.

(3 BE)

Für genau einen Wert von $a$ hat die Gerade $g_{a}$ einen Schnittpunkt mit der $x_{3}$ -Achse. Ermitteln Sie die Koordinaten dieses Schnittpunktes.

Lösung Aufgabe a)

In der Aufgabe wird der Schnittpunkt einer Geraden mit einer Koordinatenebene verlangt.

Gegeben ist die von einem Parameter $a$ abhängige Geradengleichung

g_{a} : \vec{X} = (\begin{array}{c} 2 \\ a - 4 \\ 4 \end{array}) + λ \cdot (\begin{array}{c} 2 \\ - 2 \\ 1 \end{array}); λ \in R; a \in R

Man nennt solche eine Menge von (unendlich vielen) Geraden auch eine "Geradenschar" und $a$ den "Scharparameter").

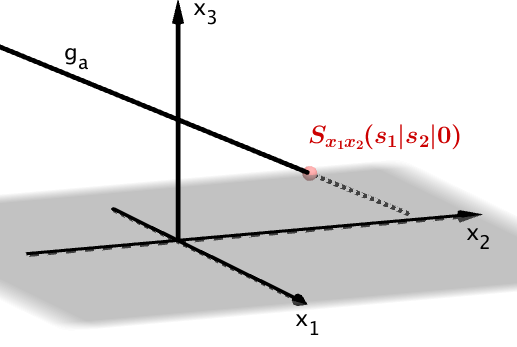
Gesucht ist der von $a$ abhängige Schnittpunkt der Schargeraden mit der Koordinatenebene $E_{x_{1} x_{2}}$ .

Eine Gerade $g_{a}$ schneidet die Koordinatenebene $E_{x_{1} x_{2}}$ dann, wenn die $x_{3}$ -Koordinate des Ortsvektors $\vec{X}$ der Geradengleichung Null ist.

Damit erhältst du folgende Vektorgleichung:

$ \begin{array}{ccll} (\begin{array}{c} x_{1} \\ x_{2} \\ 0 \end{array}) & = & (\begin{array}{c} 2 \\ a - 4 \\ 4 \end{array}) + λ \cdot (\begin{array}{c} 2 \\ - 2 \\ 1 \end{array}) & lies die 3. Zeile als Gleichung \\ 0 & = & 4 + λ \cdot 1 & löse nach λ auf \\ λ & = & - 4 \end{array}$

Mit $λ = - 4$ erhältst du den Schnittpunkt der Geradenschar $g_{a}$ mit der $x_{1} x_{2}$ -Ebene in Abhängigkeit vom Scharparameter $a$ so:

$\vec{S_{x_{1} x_{2}}} = (\begin{array}{c} 2 \\ a - 4 \\ 4 \end{array}) + (- 4) \cdot (\begin{array}{c} 2 \\ - 2 \\ 1 \end{array}) = (\begin{array}{c} - 6 \\ a + 4 \\ 0 \end{array})$

Der Schnittpunkt der Geradenschar $g_{a}$ mit der $x_{1} x_{2}$ -Ebene hat die Koordinaten $(- 6 | a + 4 | 0)$ .

Lösung Aufgabe b)

In der Aufgabe geht es um den Schnitt räumlicher Geraden mit der Lösbarkeit eines linearen Gleichungssystems.

Vorüberlegung

Eine Gerade, die zu einer Ebene nicht parallel ist, schneidet diese - wie auch Teilaufgabe a) zeigt - stets in genau einem Punkt.

Ob eine Gerade im Raum jedoch auch eine nicht zu ihr parallele Gerade schneidet, ist nicht sicher. Beide Geraden können - wie man sagt - "windschief"- zueinander verlaufen.

Du musst zeigen, dass genau eine Gerade der Schar $g_{a}$ die $x_{3}$ -Achse schneidet und somit zu ihr nicht windschief ist.

Du musst also zeigen, dass die Vektorgleichung

$(\begin{array}{c} 0 \\ 0 \\ x_{3} \end{array}) \overset{?}{=} (\begin{array}{c} 2 \\ a - 4 \\ 4 \end{array}) + λ \cdot (\begin{array}{c} 2 \\ - 2 \\ 1 \end{array})$ genau einen Wert $a$ und ein $λ$ als Lösung besitzt.

Schreibe die ersten beiden Zeilen der Vektorgleichung als ein Gleichungssystem von zwei Gleichungen mit den Unbekannten $a$ und $λ$ .

$\begin{array}{rccll} I & 0 & = & 2 + 2 λ & \Rightarrow \\ II & 0 & = & a - 4 - 2 λ \end{array}$

$λ = - 1$

$λ$ $in$ $II$ $einsetzen$

$I I^{'} 0 = a - 4 + 2 \Rightarrow a = 2$

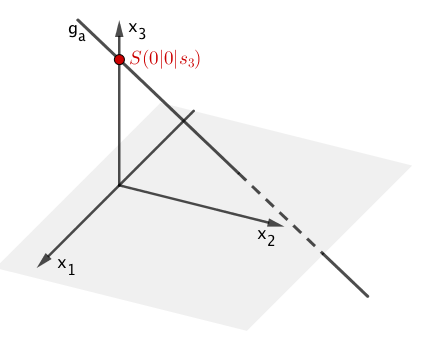
Mit $a = 2$ ergibt sich für $λ = - 1$ ein Schnittpunkt der Geraden $g_{2}$ mit der $x_{3}$ _Achse:

{\vec{S}}_{x_{3}} = (\begin{array}{c} 2 \\ 2 - 4 \\ 4 \end{array}) + (- 1) \cdot (\begin{array}{c} 2 \\ - 2 \\ 1 \end{array}) = (\begin{array}{c} 0 \\ 0 \\ 3 \end{array}) .

Also der Punkt S(0|0|3).

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das? serlo.org