Stochastik, Teil B, Aufgabengruppe 1

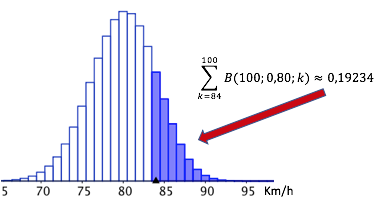
Interpretation der Angabe

Bereits in der 1. Aufgabe war gegeben, dass die Geschwindigkeitsverteilung der Messungen näherungsweise durch die Binomialverteilung $B(100;\mathrm{0,8})$ beschrieben werden kann.

Die Wahrscheinlichkeit, dass die Geschwindigkeit eines vorbeifahrenden Pkw größer als 83 km/h wird dann näherungsweise durch den Wert

erfasst.

Zur Vereinfachung darf bei der weiteren Behandlung der Aufgabe vom Wert $\mathrm{0,19}$ ausgegangen werden.

Lösung Teilaufgabe a)

$X$ sei die Zufallsgröße, welche die Anzahl der Tempoverstöße beschreibt. $X$ ist dann gemäß der Angabe nach $B(n;\mathrm{0,19})$ binomialverteilt.

Die Angabe "mindestens ein Tempoverstoß" bedeutet $X\ge 1$ und ist das Gegenereignis zu "kein Tempoverstoß", also zu $X=0$.

Damit ergibt sich folgende Ungleichung, die schrittweise nach der Unbekannten $n$ aufzulösen ist.

$$\begin{array}{rcll}{P}_{\mathrm{0,19}}^n(X\ge 1)& >& \mathrm{0,99}& |\text{Gegenereignis heranziehen}\\ 1-P_{\mathrm{0,19}}^n(X=0)& >& \mathrm{0,99}& |-1\\ -P_{\mathrm{0,19}}^n(X=0)& >& -\mathrm{0,01}& |\cdot (-1)\text{Relationszeichen wechselt!}\\ P_{\mathrm{0,19}}^n(X=0)& <& \mathrm{0,01}& |\text{Formel für Bernoulli-Kette}\\ {\displaystyle \underset{1}{\underbrace{\left(\genfrac{}{}{0px}{}{n}{0}\right)}}\cdot \underset{1}{\underbrace{{\mathrm{0,19}}^0}}\cdot (1-\mathrm{0,19}{)}^{n-0}}& <& \mathrm{0,01}& |\text{Zusammenfassen}\\ {\mathrm{0,81}}^n& <& \mathrm{0,01}& |\text{Logarithmieren, z.B. mit ln}\\ ln(\mathrm{0,81}{)}^n& <& ln(\mathrm{0,01})& |\text{Es gilt:}lo{g}_a{b}^n=n\cdot lo{g}_{a}b\\ n\cdot ln(\mathrm{0,81})& <& ln(\mathrm{0,01})& |:ln(\mathrm{0,81})<0\\ & & & \Rightarrow \text{Relationszeichen wechselt!}\\ n& >& {\displaystyle \frac{ln(\mathrm{0,01})}{ln(\mathrm{0,81})}}& \\ n& \ge & \mathrm{21,86}& |n\in \mathbb{N}\end{array}$$

Es müssen mindestens 22 Geschwindigkeitsmessungen durchgeführt werden, damit mit einer Wahrscheinlichkeit von mehr als 99% mindestens ein Tempoverstoß gemessen wird.

Lösung Teilaufgabe b)

Der Aufgabe liegt zunächst eine Zufallsgröße $X$ zugrunde, die binomial nach $B(50;\mathrm{0,19})$ verteilt ist und die Anzahl der Tempoverstöße ($v>83\text{km|h}$) misst.

Für den Erwartungswert$\mu$ von $X$ gilt:

$\mu =n\cdot p=50\cdot \mathrm{0,19}=\mathrm{9,5}$

Die Standardabweichung$\sigma$ berechnet sich so:

$\sigma =\sqrt{n\cdot p\cdot (1-p)}=\sqrt{50\cdot \mathrm{0,19}\cdot \mathrm{0,81}}\approx \mathrm{2,77}$

Interpretation im bisherigen Sachzusammenhang

Die Polizei kann erwarten, dass ihr bei 50 Messungen 9 oder 10 Temposünder "ins Netz gehen". Falls plötzlich zu wenig "Raser" durch die Messstelle fahren, vermutet sie, dass die Autofahrer - wie und warum auch immer - vorm "Blitzen" gewarnt werden und bricht den Einsatz ab.

"Zufrieden" ist sie, wenn mindestens

$\mu -\sigma =\mathrm{9,5}-\mathrm{2,77}=\mathrm{6,73}$,

also mindestens $7$ Tempoverstöße registriert werden.

Interpretation in einem neuen Sachzusammenhang

Wovon die Polizei nichts weiß: Es sind auf einmal weniger Temposünder unterwegs, nämlich nur noch $10\%$ statt $19\%$.

Ihre Entscheidungsregel, von der sie nicht abrückt, Fortführung der "Blitz-Aktion" falls $X\ge 7$, besitzt dann die Wahrscheinlichkeit $P_{\mathrm{0,1}}^{50}(X\ge 7)$.

$\begin{array}{clll}{P}_{\mathrm{0,1}}^{50}(X\ge 7)& =& 1-P_{\mathrm{0,1}}^{50}(X\le 6)& |\text{ Gegenereignis}\\ & =& 1-\mathrm{0,77023}& |\text{Tafel benutzt}\\ & =& \mathrm{0,22977}& \\ & \approx & \mathrm{23,0}\%& \end{array}$

Die Wahrscheinlichkeit, dass die Geschwindigkeitskontrolle trotz Warnung fortgeführt wird, beträgt rund $23\%$.