Stochastik, Teil B, Aufgabengruppe 2

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe-Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
$1.$ Nach einem Bericht zur Allergieforschung aus dem Jahr 2008 litt damals in Deutschland jeder vierte bis fünfte Einwohner an einer Allergie. 41 % aller Allergiker reagierten allergisch auf Tierhaare. Kann aus diesen Aussagen gefolgert werden, dass 2008 mindestens 10 % der Einwohner Deutschlands auf Tierhaare allergisch reagierten? Begründen Sie Ihre Antwort. (3 BE)
$2.$ Nach einer aktuellen Erhebung leiden $25$ % der Einwohner Deutschlands an einer Allergie. Aus den Einwohnern Deutschlands werden $n$ Personen zufällig ausgewählt.
$a$ ) Bestimmen Sie, wie groß $n$ mindestens sein muss, damit mit einer Wahrscheinlichkeit von mehr als $99$ % mindestens eine der ausgewählten Personen an einer Allergie leidet. (4 BE)
$b$ ) Im Folgenden ist $n = 200$ . Die Zufallsgröße $X$ beschreibt die Anzahl der Personen unter den ausgewählten Personen, die an einer Allergie leiden. Bestimmen Sie die Wahrscheinlichkeit dafür, dass der Wert der binomialverteilten Zufallsgröße $X$ höchstens um eine Standardabweichung von ihrem Erwartungswert abweicht. (5 BE)
$3.$ Ein Pharmaunternehmen hat einen Hauttest zum Nachweis einer Tierhaarallergie entwickelt. Im Rahmen einer klinischen Studie zeigt sich, dass der Hauttest bei einer aus der Bevölkerung Deutschlands zufällig ausgewählten Person mit einer Wahrscheinlichkeit von $39,5$ % ein positives Testergebnis liefert. Leidet eine Person an einer Tierhaarallergie, so ist das Testergebnis mit einer Wahrscheinlichkeit von $85$ % positiv. Das Testergebnis ist jedoch bei einer Person, die nicht an einer Tierhaarallergie leidet, mit einer Wahrscheinlichkeit von $35$ % ebenfalls positiv.
$a$ ) Ermitteln Sie, welcher Anteil der Bevölkerung Deutschlands demnach allergisch auf Tierhaare reagiert. (4 BE)
$b$ ) Eine aus der Bevölkerung Deutschlands zufällig ausgewählte Person wird getestet; das Testergebnis ist positiv. Berechnen Sie die Wahrscheinlichkeit dafür, dass diese Person tatsächlich an einer Tierhaarallergie leidet. (2 BE)
$c)$ Aus der Bevölkerung Deutschlands wird eine Person zufällig ausgewählt und getestet. Beschreiben Sie das Ereignis, dessen Wahrscheinlichkeit im Sachzusammenhang mit dem Term $0,09 \cdot 0,15 + 0,91 \cdot 0,35$ berechnet wird. (2 BE)

Lösung zu 1)
Betrachte folgende Ereignisse:
$A :$ Einwohner ist Allergiker.
$B :$ Einwohner ist gegen Tierhaare allergisch.
Wir wissen bereits aus den Informationen im Text:
$P (A)_{m i n} = 0,2$ bis $P (A)_{m a x} = 0,25$
("…jeder vierte bis fünfte Einwohner…Allergie.")
$P_{A} (B) = 0,41$
("…41 Prozent aller Allergiker…Tierhaare.")
Du möchtest nun wissen, ob gilt:
$P (B) \geq 0,1$
("…10 Prozent der Einwohner…Tierhaare allergisch.")
Berechne nun zunächst die Wahrscheinlichkeit des Ereignisses $A \cap B$ (Einwohner ist Allergiker und gegen Tierhaare allergisch).
Für bedingte Wahrscheinlichkeiten gilt:
$P_{A} (B) = \frac{P (A \cap B)}{P (A)} \Leftrightarrow P (A \cap B) = P (A) \cdot P_{A} (B)$
Du rechnest nun die maximale und minimale Wahrscheinlichkeit von $P (A \cap B)$ aus, in dem du jeweils $P (A)_{m i n}$ bzw. $P (A)_{m a x}$ für $P (A)$ in die Formel von oben einsetzt. Es folgt:
$P {(A \cap B)}_{\min} = 0,2 \cdot 0,41 = 0,082 = 8,2 %$
$P {(A \cap B)}_{\max} = 0,25 \cdot 0,41 = 0,1025 = 10,25 %$
Im vorliegenden Fall gilt weiter die Beziehung $P (A \cap B) = P (B)$ , da das Ereignis $P (A \cap B)$ die Wahrscheinlichkeit $0$ hat (jeder Tierhaarallergiker ist schließlich allergisch). Solltest du das nicht sehen, dann kannst du auch mit einer Vierfeldertafel darauf kommen.
Es gilt also:
$P {(B)}_{\min} = 8,2 %$
$P {(B)}_{\max} = 10,25 %$
Antwort: Aus den beiden Aussagen kann nicht gefolgert werden, dass mindestens $10$ Prozent aller Einwohner auf Tierhaare allergisch sind.
Lösung zu Aufgabe 2a)
Definiere zunächst eine geeignete Zufallsgröße:
$X :$ Anzahl der Personen mit Allergie unter $n$ Einwohner.
Es gilt: Die Wahrscheinlichkeit, dass eine zufällig ausgewählte Person eine Allergie hat, beträgt $0,25$ . Weiter handelt es sich beim vorliegenden Zufallsexperiment im Urnenmodell betrachtet um den Fall "Ziehen mit Zurücklegen".
Aus diesen Überlegungen folgt, dass die Zufallsgröße $X$ binomialverteilt ist mit den Parametern $n$ und $0,25$ .
Nun möchtest du $n$ bestimmen, so dass gilt:
$P (X \geq 1) > 0,99$
Mit der Beziehung $P (X \geq 1) = 1 - P (X = 0)$ folgt:
$P (X = 0) < 0,01$
Nun setzt du für $P (X = 0)$ die entsprechende Bernoulli-Kette ein.
Du erhältst:
$(\binom{n}{0}) \cdot {0,25}^{0} \cdot {0,75}^{n - 0} < 0,01$
Nun muss noch nach $n$ aufgelöst werden:
${0,75}^{n - 0}$ $<$ $0,01$ $\ln$
$\ln {0,75}^{n}$ $<$ $\ln 0,01$
↓
Logarithmusrechenregeln
$n \cdot \ln 0,75$ $<$ $\ln 0,01$
↓
Achtung: Vorzeichen drehen sich bei der Multiplikation mit negativen Zahlen um.
$n$ $>$ $\frac{\ln 0,01}{\ln 0,75}$
$>$ $16,01$
Antwort: Man benötigt mindestens $17$ Personen.
Lösung zu Aufgabe 2b)
Du entnimmst aus der Aufgabenstellung, dass $X$ die Wahrscheinlichkeitsfunktion $B (200; 0,25)$ hat.
Du sollst nun die Wahrscheinlichkeit berechnen, dass $X$ höchstens um eine Standardabweichung $σ_{X}$ vom Erwartungswert $E (X)$ abweicht. Mathematisch ausgedrückt:
$P (| X - E (X) | \leq σ_{X})$
Erwartungswert und Standardabweichung bestimmen
Für den Erwartungswert einer binomialverteilten Zufallsgröße $Y$ gilt $E (Y) = n \cdot p$ . Es folgt:
$E (X) = 200 \cdot 0,25 = 50$
Für die Standardabweichung einer binomialverteilten Zufallsgröße $Y$ gilt $σ_{Y} = \sqrt{n p (1 - p)}$ . Es folgt:
$σ_{X} = \sqrt{200 \cdot 0,25 \cdot 0,75} = \sqrt{37,5} \approx 6,1$
Wahrscheinlichkeit ausrechnen
Du formst jetzt $P (| X - E (X) | \leq σ_{X})$ um, so dass du das Tafelwerk verwenden kannst.
Es gilt:
$P (| X - E (X) | \leq σ_{X}) = P (- σ_{X} + E (X) \leq X \leq σ_{X} + E (X)) = P (X \leq σ_{X} + E (X)) - P (X < E (X) - σ_{X})$
Mit eingesetzten Werten also:
$P (X \leq 56,1) - P (X < 43,9) = P (X \leq 56) - P (X \leq 43) = 0,8555 - 0,1438 \approx 0,71$ .
Antwort: Die Wahrscheinlichkeit beträgt $71$ Prozent.
Lösung zu Teilaufgabe 3a)
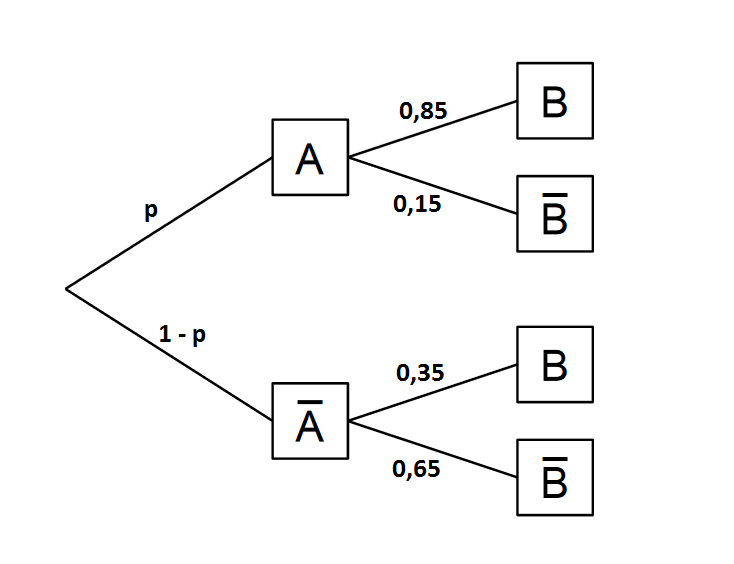
Das Stichwort zu dieser Aufgabe ist das Baumdiagramm.
Zunächst musst du dir überlegen, welche beiden Ereignisse hier betrachtet werden. Man liest aus dem Text:
$A :$ Person leidet an Tierhaarallergie.
$B :$ Hauttest liefert positives Testergebnis.
Erstelle nun ein Baumdiagramm und trage die Wahrscheinlichkeiten aus dem Text dort ein.
$P (B) = 0,395$
$P_{A} (B) = 0,85$
$P_{A} (B) = 0,35$
$P (A) = p$
Du möchtest den Wert $p$ der Wahrscheinlichkeit $P (A)$ berechnen. Verwende dafür die zweite Pfadregel:
$P (B) = p \cdot P_{A} (B) + (1 - p) \cdot P_{A} (B)$
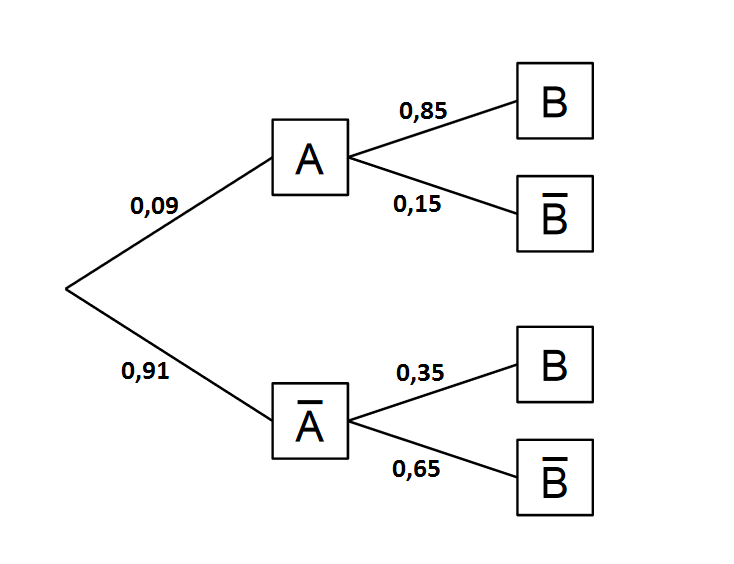
Aus dem Baumdiagramm kannst du dir die relevanten Wahrscheinlichkeiten rauslesen. Es folgt:
$0,395 = p \cdot 0,85 + (1 - p) \cdot 0,35$
Stelle noch nach $p$ um. Du erhältst:
$p = 0,09$
Antwort: Die Anteil der Bevölkerung mit Tierhaarallergie beträgt $9$ Prozent.
Lösung zu Teilaufgabe 3b)
Gesucht ist die Wahrscheinlichkeit von Ereignis $A$ für den Fall, dass Ereignis $B$ schon eingetreten ist. In mathematischer Schreibweise ausdrückt also die bedingte Wahrscheinlichkeit $P_{B} (A)$ .
Nun gilt per Definition für bedingte Wahrscheinlichkeiten folgende Beziehung:
$P_{B} (A) = \frac{P (B \cap A)}{P (B)}$
Aus dem Baumdiagramm der vorherigen Aufgabe lässt sich $P (B \cap A)$ einfach ausrechnen. $P (B)$ ist bereits bekannt. Es folgt:
$P_{B} (A) = \frac{0,09 \cdot 0,85}{0,395} \approx 0,19$
Antwort: Die Wahrscheinlichkeit, dass eine positiv getestete Person tatsächlich an einer Tierallergie leidet, beträgt ungefähr $19$ Prozent.
Lösung zu Teilaufgabe 3d)
Betrachte die linke und rechte Seite des Terms $0,09 \cdot 0,15 + 0,91 \cdot 0,35$ zunächst seperat.
Es ist in diesem Fall hilfreich, das Baumdiagramm aus der Teilaufgabe $a)$ zu verwenden.
linker Term
Die linke Seite des Terms entspricht laut Baumdiagramm dem Ereignis $A \cap B$ .
Interpretation: Eine Person leidet an einer Tierallergie und hat ein negatives Testergebnis.
rechter Term
Die rechte Seite des Terms entspricht laut Baumdiagramm dem Ereignis $A \cap B$ :
Interpretation: Eine Person leidet nicht an der Tierallergie und hat ein positives Testergebnis.
gesamter Term
Die Summe der beiden Terme entspricht also dem Ereignis $(A \cap B) \cup (A \cap B)$ .
Interpretation: Eine Person erhält ein falsches Testergebnis.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org

${0,75}^{n - 0}$	$<$	$0,01$	$\ln$
$\ln {0,75}^{n}$	$<$	$\ln 0,01$
	↓	Logarithmusrechenregeln
$n \cdot \ln 0,75$	$<$	$\ln 0,01$
	↓	Achtung: Vorzeichen drehen sich bei der Multiplikation mit negativen Zahlen um.
$n$	$>$	$\frac{\ln 0,01}{\ln 0,75}$
	$>$	$16,01$

Stochastik, Teil B, Aufgabengruppe 2

Lösung zu 1)

Lösung zu Aufgabe 2a)

Lösung zu Aufgabe 2b)

Erwartungswert und Standardabweichung bestimmen

Wahrscheinlichkeit ausrechnen

Lösung zu Teilaufgabe 3a)

Lösung zu Teilaufgabe 3b)

Lösung zu Teilaufgabe 3d)

linker Term

rechter Term

gesamter Term