Teil 1 Analysis: ohne Hilfsmittel

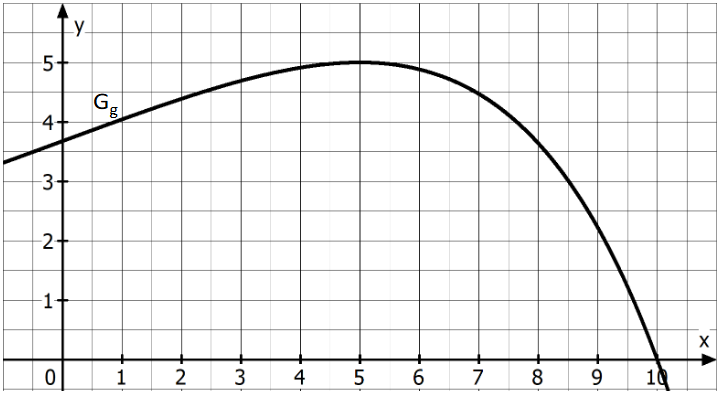
Geben Sie jeweils an, ob die folgenden Terme Werte haben, die größer, kleiner oder gleich Null sind:

a) $g(10)$ b) $g^{\prime \prime }(5)$

(2 BE)

Bestimmen Sie anhand der Abbildung graphisch die Steigung der Tangente an $G_g$ im Punkt $P(7|g(7))$. Veranschaulichen Sie Ihr Vorgehen in obiger Abbildung durch ein geeignetes Steigungsdreieck. (3 BE)

Die Funktion $g$ ist durch die Gleichung $g(x)=-(x-10)\cdot e^{\mathrm{0,2}x-1}$ gegeben. Weisen Sie nach, dass die Funktion $G:x\to -(5x-75)\cdot e^{\mathrm{0,2}x-1}$ mit $D_g=ℝ$ eine Stammfunktion von $g$ ist. (3 BE)

Berechnen Sie die ungerundeten Funktionswerte $G(5)$ und $G(10)$. Markieren Sie in der Abbildung aus a) das Flächenstück, dessen Flächenmaßzahl gleich der Differenz $G(10)-G(5)$ist und geben Sie die Maßzahl exakt an. (3 BE)

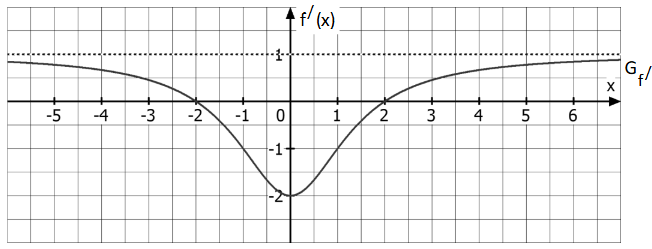
Geben Sie jeweils die Art und die x-Koordinaten der beiden relativen Extrempunkte von $G_f$ an. (3 BE)

Der Graph $G_f$ hat eine Stelle mit größtem Gefälle. Geben Sie sowohl diese Stelle als auch den Wert des größten Gefälles an. (2 BE)

Der Graph $G_f$ der Funktion $f$ besitzt für $x\to \infty$ eine Asymptote. Geben Sie die Art und die Steigung dieser Asymptote an und begründen Sie Ihre Antworten. (2 BE)