A II

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe-Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Gegeben ist die Funktion $f : x \mapsto \frac{1}{5} (x^{4} - 8 x^{3} + 18 x^{2})$ mit der Definitionsmenge $D_{f} = ℝ$ . Der Graph wird mit $G_{f}$ bezeichnet.
Untersuchen Sie das Symmetrieverhalten von $G_{f}$ bezüglich des Koordinatensystems und geben Sie das Verhalten von $f (x)$ für $x \to - \infty$ und für $x \to \infty$ an.

Zeigen Sie, dass die Funktion $f$ genau eine Nullstelle besitzt und geben Sie diese samt Vielfachheit an.

Begründen Sie nur mithilfe der Ergebnisse aus 1.a und 1.b, dass an der Stelle $x = 0$ ein relatives und zugleich absolutes Minimum von $f$ vorliegen muss.

Zeigen Sie, dass an den Stellen $x = 1$ und $x = 3$ Wendestellen von $f$ liegen. Ermitteln Sie auch die Koordinaten der zugehörigen Punkte und welcher der beiden Punkte ein Terrassenpunkt ist.

Die Wendepunkte aus Teilaufgabe 1.d legen die Gerade $G_{g}$ fest. Ermitteln Sie deren Glei-chung.

Zeichnen Sie die Graphen $G_{f}$ und $G_{g}$ unter Mitverwendung vorliegender Ergebnisse im Bereich $- 1 \leq x \leq 4,5$ in ein kartesisches Koordinatensystem.
Maßstab: 1 LE = 1 cm.

Die Graphen $G_{f}$ und $G_{g}$ schließen drei endliche Flächenstücke ein. Schraffieren Sie das mittlere Flächenstück in Ihrer Zeichnung von Aufgabe 1.f und berechnen Sie die Maßzahl seines Flächeninhaltes.
2
Gegeben ist der Graph der 1. Ableitung $h^{'}$ der Funktion $h$ mit der Definitionsmenge $D_{h} = ℝ$ .
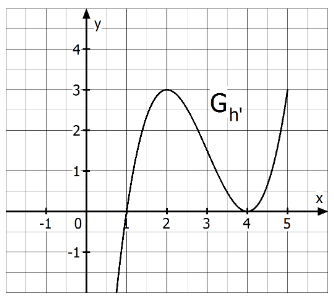
Bestätigen oder widerlegen Sie begründet folgende Aussagen:
a) $G_{h}$ hat einen Tiefpunkt bei $x = 1$ .
b) $G_{h}$ hat einen Tiefpunkt bei $x = 4$ .
c) $G_{h}$ hat einen Wendepunkt bei $x = 2$ .
d) Die Tangente an den Graphen $G_{h}$ in $x = 2$ verläuft parallel zur Geraden $e$ mit der Gleichung $y = 3 x + 7$ .
3
Gegeben sind die reellen Funktionen $k_{a} : x \mapsto \frac{1}{9} (x^{4} - 2 a x^{3})$ mit $x, a \in ℝ$ und $a \geq 0$ . Ermitteln Sie Art und Koordinaten der relativen Extrempunkte der zugehörigen Graphen $G_{k_{a}}$ in Abhängigkeit von $a$ .
4
Auf der Außenwand eines neuen Hallenbades soll dessen Logo, eine Welle, abgebildet werden. Der Architekt möchte ein großes Fenster in Form eines rechtwinkligen Dreiecks (siehe Skizze $∆ P Q R$ ) innerhalb der Welle anbringen.
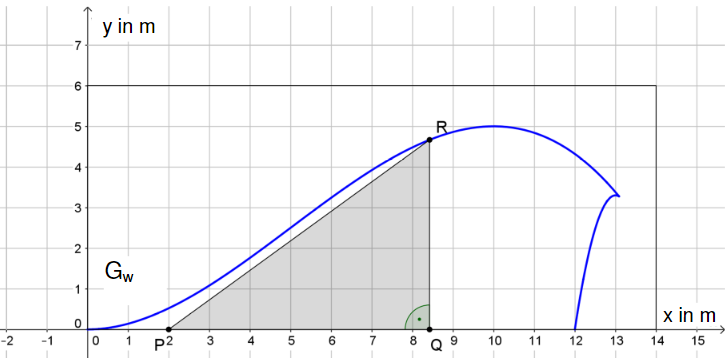
Das Fenster soll am Punkt $P (2 | 0)$ beginnen. Seine Breite | $P Q$ | soll mindestens $5 m$ und höchstens $10 m$ betragen. Der Punkt $R$ soll auf der oberen Begrenzungslinie (Graph $G_{w}$ ) der Welle liegen, welche durch die Funktion $w : x \mapsto - 0,01 x^{3} + 0,15 x^{2}$ beschrieben wird. Bei Berechnungen kann auf Einheiten verzichtet werden.
Zeigen Sie, dass die Maßzahl $A$ der Fläche des Fensters abhängig von der $x$ -Koordinate des Punktes $Q$ durch die Funktionsgleichung $A (x) = 0,005 (- x^{4} + 17 x^{3} - 30 x^{2})$ beschrieben wird, und geben Sie für die Funktion $A$ einen Definitionsbereich $D_{A}$ an, der den Vorgaben von Aufgabe 4 entspricht.

Der Architekt möchte das Hallenbad möglichst hell gestalten. Aus diesem Grund soll die Fläche des Fensters möglichst groß sein. Bestimmen Sie die $x$ -Koordinate des Punktes $Q$ , für welche die Maßzahl der Fläche $A$ maximal wird. Berechnen Sie für diesen Fall Breite, Höhe und Fläche des Fensters. Ermitteln Sie den prozentualen Anteil der Fensterfläche an der Logofläche, wenn diese $36 m^{2}$ beträgt. Runden Sie Ihre Ergebnisse auf zwei Nachkommastellen.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org