Teil 2 Analysis I

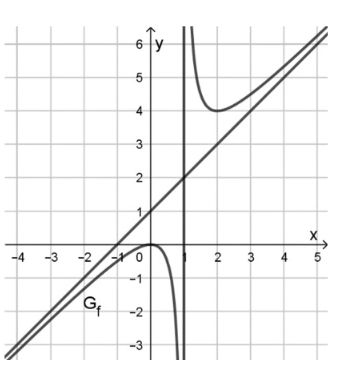
Bestätigen Sie die schiefe Asymptote von $G_f$ und die Nullstelle von $f$ durch Rechnung.

Geben Sie mithilfe der Abbildung die maximalen Monotonieintervalle sowie die Wertemenge der Funktion $f$ an. Entnehmen Sie hierzu der Abbildung ganzzahlige Werte.

Entscheiden Sie, ob die Funktion $g$ Nullstellen besitzt und begründen Sie Ihre Entscheidung.

Untersuchen Sie das Verhalten der Funktionswerte von $g$ an den Rändern der Definitionsmenge und geben Sie die Gleichung der Asymptote von $G_g$ an.

Bestimmen Sie Art und Koordinaten des Extrempunktes von $G_g$.

Zeichnen Sie den Graphen $G_g$ und seine Asymptoten unter Verwendung der bisherigen Ergebnisse und weiterer geeigneter Funktionswerte für $1<x\le 6$ in ein kartesisches Koordinatensystem.

Gegeben ist die Stammfunktion G : $x\mapsto -x+2x\cdot \ln (x)-(x-1)\cdot \ln (x-1)$ mit $D_g=]1;+\infty [$ der Funktion $g$ (Nachweis nicht erforderlich). Berechnen Sie die Maßzahl des Flächenstücks, das von $G_g$, der x-Achse sowie den beiden Geraden mit den Gleichungen $x=2$ und $x=3$ eingeschlossen wird. Runden Sie Ihr Ergebnis auf zwei Nachkommastellen und kennzeichnen Sie das Flächenstück im Koordinatensystem der Teilaufgabe 2.d.

Ermitteln Sie, nach wie vielen Stunden nach der Einnahme gemäß der gewählten Modellfunktion die maximale Konzentration des Medikamentes im Blut erreicht ist und berechnen Sie diese maximale Konzentration.

Berechnen Sie mithilfe partieller Integration den Wert des bestimmten Integrals $${\displaystyle {\displaystyle \frac{1}{20}}{\int }_0^{20}k(t)\mathrm{d}t}$$ und interpretieren Sie das Ergebnis im Sachzusammenhang.

Zeichnen Sie den Graphen der Funktion $k$ in ein kartesisches Koordinatensystem im Intervall $0\le t\le 25$. Maßstab für beide Achsen: $1$ LE $=\mathrm{0,5}\text{ cm}.$ Übersteigt die Konzentration des verabreichten Medikaments im Blut des Patienten $6{\displaystyle \frac{\text{mg}}{\text{ l}}}$ können Nebenwirkungen auftreten. Ermitteln Sie näherungsweise mit Hilfe des Graphen von $k$, in welchem Zeitraum nach der Einnahme damit zu rechnen ist.

Um die Nebenwirkungen zu vermindern, plant der Hersteller das Medikament geringer zu dosieren. Es soll vier Stunden nach der Einnahme als Höchstwert eine Konzentration von $56{\displaystyle \frac{\text{mg}}{\text{ l}}}$ im Blut auftreten. Die Konzentration im Blut lässt sich dann mit einer Funktionsgleichung der Art $g(t)=c\cdot t\cdot e^{-\mathrm{0,25}t+2}$ mit $t\in {ℝ}_{\mathrm{𝟘}}^{+}$ und $c\in ℝ$ modellhaft darstellen. Dabei gibt der Funktionswert von $g$ die Konzentration des Medikaments im Blut des Patienten in Milligramm pro Liter $6{\displaystyle \frac{\text{mg}}{\text{ l}}}$ und die Variable $t$ die Zeit in Stunden $[\text{ h}]$ nach der Einnahme an.

1. Bestimmen Sie den Wert des Parameters $c$.

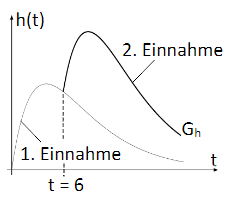
2. Einem Patienten wird verordnet, sechs Stunden nach der Ersteinnahme das Medikament nochmals einzunehmen. Die Konzentration im Blut entspricht dann modellhaft den Funktionswerten der Funktion $h$ mit $h(t)=\mathrm{0,46}t\cdot e^{-\mathrm{0,25}t+2}+\mathrm{0,46}(t-6)e^{-\mathrm{0,25}(t-6)+2}$ mit $t\in ℝ$ und $t\ge 6$. Die Abbildung zeigt den Graphen $G_h$ der Funktion $h$. Untersuchen Sie, ob der Patient bei dieser Verordnung mit Nebenwirkungen (siehe Teilaufgabe 3.c) zu rechnen hat.