B I

Die vier Bauern sind untereinander und mit dem Markt nach dem Leontief-Modell verbunden. Die Inputmatrix ist

$A=\left(\begin{array}{cccc}\mathrm{0,6}& \mathrm{0,1}& \mathrm{0,05}& \mathrm{0,05}\\ \mathrm{0,07}& \mathrm{0,7}& 0& \mathrm{0,03}\\ \mathrm{0,1}& \mathrm{0,1}& \mathrm{0,3}& \mathrm{0,1}\\ \mathrm{0,2}& \mathrm{0,05}& \mathrm{0,15}& \mathrm{0,5}\end{array}\right)$

Die Gesamtproduktion von $\text{KI}$ beträgt $200$ ME (Mengeneinheiten), diejenige von $\text{ER}$ $600$ ME. Übertragen Sie das Verflechtungsdiagramm (siehe unten) auf Ihren Bearbeitungsbogen, berechnen Sie alle fehlenden Zahlenwerte und tragen Sie diese in Ihr Diagramm ein.

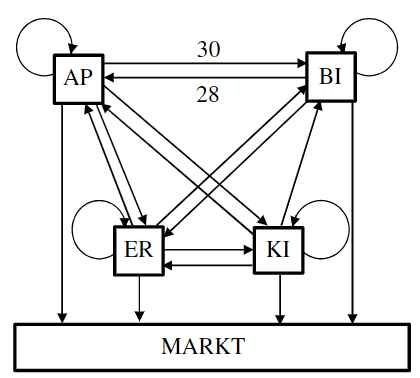
Nach der Erdbeer-Saison steigt Bauer $\text{ER}$ aus dem gemeinsamen Tausch aus, während $AP$, $BI$ und $KI$ weiter zusammenarbeiten. Für die neue, veränderte Inputmatrix $A$* gilt: $A$*= $\left(\begin{array}{ccc}\mathrm{0,6}& \mathrm{0,1}& \mathrm{0,05}\\ \mathrm{0,07}& \mathrm{0,7}& 0\\ 0& \mathrm{0,1}& \mathrm{0,3}\end{array}\right)$

(1) Die Produktionszahlen ändern sich zum Saisonende und werden durch den Produktionsvektor $\overrightarrow{x}=\left(\begin{array}{c}700+2k\\ 600\\ 150-k\end{array}\right)$ mit $k\in {ℝ}_0^{+}$ dargestellt. Berechnen Sie die Produktionsmengen der Bauern, wenn $\text{BI}$ $124$ ME an den Markt abgibt.

(2) Nach strukturellen Veränderungen in den Betrieben kalkulieren die Bauern $\text{AP}$, $\text{BI}$ und $\text{KI}$ für die kommende Saison eine Marktabgabe von $351$ ME an Äpfeln, $157$ ME Birnen und $76$ ME Kirschen. Bestimmen Sie die Mengen an Obst, die die Bauern bei gleichbleibender Verflechtung jeweils produzieren müssten, um die Konsummengen zu erreichen.

Die Punkte $A$ und $B$ legen die Gerade $g$ fest, die Punkte $C_k$ liegen auf der Geraden $h$. Geben Sie jeweils eine Gleichung der beiden Geraden an und untersuchen Sie die gegenseitige Lage der beiden Geraden.

Für die folgenden Teilaufgaben gilt $k=-3$. Es ergibt sich $C_{-3}-(\text{–}3|\text{–}5|3)$.

(1) Die Punkte $A,B$ und $C_{-3}$ legen die Ebene $E$ fest. Bestimmen Sie je eine Gleichung der Ebene $E$ in Parameter- und Koordinatenform.

[ mögliches Teilergebnis: $E:x_1+x_2+3x_3-1=0$]

(2) Untersuchen Sie die Lagebeziehung der Ebene $E$ mit der Ebene $F:\overrightarrow{x}=\left(\begin{array}{c}2\\ 2\\ -1\end{array}\right)+r\cdot \left(\begin{array}{c}-5\\ -7\\ 4\end{array}\right)+t\cdot \left(\begin{array}{c}1\\ 3\\ 6\end{array}\right)$ mit $r,t\in ℝ$ und bestimmen Sie gegebenenfalls eine Gleichung der Schnittgeraden.

(3) Die Punkte $A,B,C_{-3}$ und $D(3|5|5)$ legen ein Tetraeder fest (siehe Skizze).

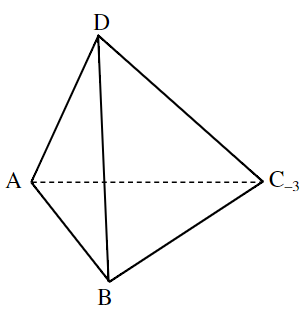
Spiegelt man den Punkt $C_3$ am Punkt $D$, so erhält man den Punkt $C_{-3}^{\ast }$. Berechnen Sie die Koordinaten des Punktes $C_{-3}^{\ast }$.

(4) Der Punkt $C_{-3}^{\ast }$ liegt in der Ebene $F$ (Nachweis nicht erforderlich). Eine der Seitenflächen des Tetraeders liegt ganz in der Ebene $F$. Entscheiden Sie, welche der Flächen das ist und begründen Sie Ihre Entscheidung.

(5) Der Punkt $S(-{\displaystyle \frac{1}{3}}|-{\displaystyle \frac{5}{3}}|1)$ ist Schwerpunkt des Dreiecks $AB{C}_{-3}$, der Punkt $M$ ist Mittelpunkt der Kante $\overline{AB}$und der Punkt $N$ ist Mittelpunkt der Kante $\overline{D{C}_{-3}}$. Die Gerade $MN$ und die Gerade $DS$ schneiden sich im Punkt $P$. Berechnen Sie Koordinaten des Punktes $P$.