Pflichtteil - Analysis & Analytische Geometrie / Lineare Algebra

🎓 Prüfungsbereich für Niedersachsen

Weitere Bundesländer & Aufgaben:
Mathe-Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Wichtig: Für die Aufgaben hier gelten andere Nutzungbedingungen.

1
Aufgabe P1
Die Abbildung zeigt den Graphen der
Funktion $f$ mit $f (x) = a \cdot b^{x}$ mit $a > 0$ und $b > 0$ .
Bestimmen Sie die passenden Werte von $a$ und $b$ . (3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktion
Anfangswert $a$
Bei $y = 0,5$ verläuft der Graph durch die y-Achse. Damit ist der Anfangswert $a = 0,5$ .
Wachstumsrate $b$
Lies einen weiteren Punkt des Graphen wie $P (1 | 2)$ aus dem Koordinatensystem ab. Wir setzen ihn in die Funktionsgleichung ein:
$f (x)$ $=$ $0,5 \cdot b^{x}$
↓
Punkt einsetzen
$2$ $=$ $0,5 \cdot b^{1}$ $: 0,5$
$4$ $=$ $b$
Damit ist die Funktionsgleichung: $f (x) = 0,5 \cdot 4^{x} $
Bestimme den Anfangswert $a$ mithilfe der Stelle, an der der Graph durch die y-Achse geht.
Bestimme $b$ mit einem weiteren Punkt des Graphen.

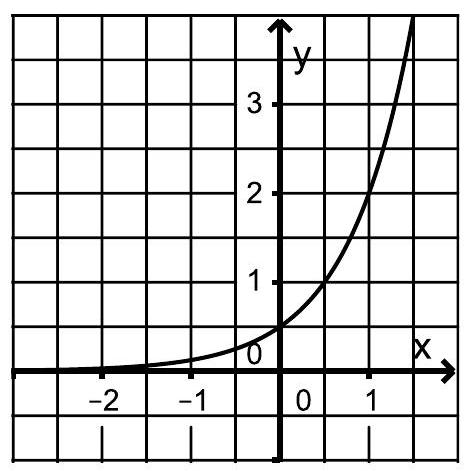
Der Graph der in $ℝ$ definierten Funktion $g$ mit $g (x) = 3^{x}$ wird um $2$ in negative $x$ -Richtung verschoben.
Zeigen Sie, dass der dadurch entstehende Graph auch durch eine Streckung des Graphen von $g$ in $y$ -Richtung erzeugt werden kann. (2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzgesetze
Verschiebung um $2$ in negativer $x$ -Richtung
$g (x) = 3^{x + 2}$
Umformung von $g (x)$
$g (x) = 3^{x + 2} = 3^{x} \cdot 3^{2} = 9 \cdot 3^{x}$
Somit kann $g (x)$ auch durch eine Streckung in $y$ -Richtung um den Faktor $9$ erzeugt werden.
Verschiebe die Funktion um $2$ in negative $x$ -Richtung.
Wende die Potenzgesetze an.
2
Aufgabe P2
Eine ganzrationale Funktion $f$ hat die Nullstellen $1$ , $2$ und $- 3.$
Geben Sie eine Funktionsgleichung für $f$ an. (2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Linearfaktorzerlegung durchführen
Linearfaktoren bilden
Linearfaktor für $x = 1$ $\Rightarrow$ $(x - 1)$
Linearfaktor für $x = 2$ $\Rightarrow$ $(x - 2)$
Linearfaktor für $x = - 3$ $\Rightarrow$ $(x + 3)$ , da $(- (- 3) = 3)$
Linearfaktordarstellung
$f (x) = (x - 1) (x - 2) (x + 3)$
Ausmultiplizieren
$f (x)$ $=$ $(x^{2} - 3 x + 2) (x + 3)$
$f {(x)}_{}$ $=$ $x^{3} + 3 x^{2} - 3 x^{2} - 9 x + 2 x + 6$
$f (x)$ $=$ $x^{3} - 7 x + 6$
Also ist eine mögliche Funktionsgleichung für die gegebene ganzrationale Funktion $f (x) = x^{3} - 7 x + 6.$
Bilde die Linearfaktoren.
Multipliziere die Linearfaktoren, um die Linearfaktordarstellung zu erhalten.
Multipliziere aus, um die Funktionsgleichung zu erhalten.

Für eine Funktion $h$ gilt: $h^{'} (x) = x^{2} - 2 x - 24$
Bestimmen Sie die Extremstellen des Graphen von $h$ . (3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
Nullstellen berechnen
$x^{2} - 2 x - 24$ $=$ $0$
↓
$p q - F o r m e l$
$x_{1,2}$ $=$ $- \frac{(- 2)}{2} \pm \sqrt{{(\frac{(- 2)}{2})}^{2} - (- 24)}$
$x_{1,2}$ $=$ $1 \pm \sqrt{{(1)}^{2} + 24}$
$x_{1,2}$ $=$ $1 \pm \sqrt{25}$
$x_{1} = - 4$
$x_{2} = 6$
$2$ . Ableitung
$h^{''} (x) = 2 x - 2$
Hinreichende Bedingung
$h^{''} (- 4) = 2 \cdot (- 4) - 2 = - 10$
$h^{''} (6) = 2 \cdot 6 - 2 = 10$
Da beide ungleich Null sind , sind $x_{1} = - 4$ und $x_{2} = 6$ Extremstellen des Graphen von $h$ .
Bestimme die Nullstellen der Ableitung $h^{'}$ .
Prüfe die hinreichende Bedingung mit Hilfe der $2$ . Ableitung.
3
Aufgabe P3
Gegeben ist die in $ℝ$ definierte Funktion $f$ mit $f (x) = x^{2}$ .
Bestimmen Sie diejenige reelle Zahl $m$ mit $m < 0$ , für die der Graph von $f$ und die Gerade mit der Gleichung $y = m \cdot x$ eine Fläche mit dem Inhalt $36$ einschließen. (5 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Integrale
Schnittpunkte berechnen
$f (x) = x^{2}$
$y = m \cdot x$
Setzen wir sie gleich:
$m x$ $=$ $x^{2}$
$0$ $=$ $x^{2} - m x$
$=$ $x (x - m)$
Die Schnittpunkte befinden sich an den Stellen $x = 0$ und $x = m$ . Diese Stellen bilden die Grenzen des Integrals. Da $m < 0$ ist $m$ die linke Grenze.
Fläche berechnen
Die Fläche zwischen den Kurven ist gegeben durch:
"obere Funktion minus untere Funktion"
↓
$A$ $=$ $\int_{m}^{0} m x - x^{2} d x$
↓
Stammfunktion bilden
$=$ ${[\frac{m}{2} x^{2} - \frac{1}{3} x^{3}]}_{m}^{0}$
↓
Grenzen einsetzen
$=$ $0 - (\frac{m^{3}}{2} - \frac{m^{3}}{3})$
$=$ $- \frac{m^{3}}{6}$
Die Fläche zwischen den Graphen beträgt $A = | - \frac{1}{6} m^{3} | = \frac{1}{6} | m^{3} | = \frac{1}{6} | m |^{3}$
Fläche mit dem Inhalt $36$
Diese Fläche soll $36$ betragen: $- \frac{m^{3}}{6} = 36 \Leftrightarrow m = - 6$
Berechne die Schnittpunkte der beiden Funktionen.
Löse das Integral mit den Schnittpunkten als Grenzen.
Setze die Fläche gleich $36$ und löse die Gleichung.
4
Aufgabe P4
Gegeben sind die Punkte $A (0 | 0 | 0), B (8 | 6 | 0)$ und $C (4 | 3 | z)$ , wobei $z$ eine positive reelle Zahl ist.
Zeigen Sie, dass es sich bei dem Dreieck $A B C$ um ein gleichschenkliges Dreieck mit der Basis $A B$ handelt. (2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichschenkliges Dreieck
Vektoren bilden
$A (0 | 0 | 0), B (8 | 6 | 0) \Rightarrow \vec{A B} = (\begin{array}{c} b_{1} - a_{1} \\ b_{2} - a_{2} \\ b_{3} - a_{3} \end{array}) = (\begin{array}{c} 8 - 0 \\ 6 - 0 \\ 0 - 0 \end{array}) = (\begin{array}{c} 8 \\ 6 \\ 0 \end{array})$
$A (0 | 0 | 0), C (4 | 3 | z) \Rightarrow \vec{A C} = (\begin{array}{c} c_{1} - a_{1} \\ c_{2} - a_{2} \\ c_{3} - a_{3} \end{array}) = (\begin{array}{c} 4 - 0 \\ 3 - 0 \\ z - 0 \end{array}) = (\begin{array}{c} 4 \\ 3 \\ z \end{array})$
$B (8 | 6 | 0), C (4 | 3 | z) \Rightarrow \vec{B C} = (\begin{array}{c} c_{1} - b_{1} \\ c_{2} - b_{2} \\ c_{3} - b_{3} \end{array}) = (\begin{array}{c} 4 - 8 \\ 3 - 6 \\ z - 0 \end{array}) = (\begin{array}{c} - 4 \\ - 3 \\ z \end{array})$
Länge berechnen
$| \vec{A B} | = | (\begin{array}{c} 8 \\ 6 \\ 0 \end{array}) | = \sqrt{8^{2} + 6^{2} + 0^{2}} = \sqrt{100} = 10$
$| \vec{A C} | = | (\begin{array}{c} 4 \\ 3 \\ z \end{array}) | = \sqrt{4^{2} + 3^{2} + z^{2}} = \sqrt{25 + z^{2}}$
$| \vec{B C} | = | (\begin{array}{c} - 4 \\ - 3 \\ z \end{array}) | = \sqrt{(- 4)^{2} + (- 3)^{2} + z^{2}} = \sqrt{25 + z^{2}}$
Da $\vec{A C}$ und $\vec{B C}$ gleich lang sind, ist das Dreieck $A B C$ gleichschenklig und die Basis ist $A B$ .
Bilde die Vektoren der Seiten des Dreiecks.
Berechne die Längen der Vektoren.

Das Dreieck $A B C$ hat den Flächeninhalt $35$ .
Bestimmen Sie den Wert von $z$ . (3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächeninhalte und Volumen im kartesischen Koordinatensystem
Flächeninhalt berechnen
Für die Vektoren $\vec{A B} = (\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}), \vec{A C} = (\begin{array}{c} y_{1} \\ y_{2} \\ y_{3} \end{array})$ lässt sich der Flächeninhalt eines Dreiecks im Dreidimensionalen mit folgender Formel berechnen:
$A_{A B C} = \frac{1}{2} | \vec{AB} \times \vec{AC} | = \frac{1}{2} | (\begin{array}{c} x_{2} y_{3} - x_{3} y_{2} \\ x_{3} y_{1} - x_{1} y_{3} \\ x_{1} y_{2} - x_{2} y_{1} \end{array}) | = \frac{1}{2} \sqrt{{(x_{2} y_{3} - x_{3} y_{2})}^{2} + {(x_{3} y_{1} - x_{1} y_{3})}^{2} + {(x_{1} y_{2} - x_{2} y_{1})}^{2}}$
$\vec{A B} = (\begin{array}{c} 8 \\ 6 \\ 0 \end{array})$ und $\vec{A C} = (\begin{array}{c} 4 \\ 3 \\ z \end{array})$
$\begin{array}{l} \Rightarrow \frac{1}{2} | \vec{AB} \times \vec{AC} | = \frac{1}{2} | (\begin{array}{c} 6 \cdot z - 0 \cdot 3 \\ 0 \cdot 4 - 8 \cdot z \\ 8 \cdot 3 - 6 \cdot 4 \end{array}) | = \frac{1}{2} | (\begin{array}{c} 6 z \\ - 8 z \\ 0 \end{array}) | \\ = \frac{1}{2} \sqrt{{(6 z)}^{2} + {(- 8 z)}^{2} + {(0)}^{2}} = \frac{1}{2} \sqrt{36 z^{2} + 64 z^{2}} = \frac{1}{2} \sqrt{100 z^{2}} = \frac{1}{2} \cdot 10 z = 5 z \end{array}$
Hinweis: Hier ist $\sqrt{z^{2}} = z$ , da $z$ nach Aufgabenstellung positiv ist.
Flächeninhalt gleich 35
$5 z$ $=$ $35$ $: 5$
$z$ $=$ $7$
Der Wert von $z$ beträgt also $7$ .
Berechne den Flächeninhalt des Dreiecks.
Setze den Flächeninhalt gleich $35$ und löse die Gleichung.
5
Aufgabe P5
Gegeben sind die Punkte $P (2 | 0 | 1)$ und $Q (2 | 4 | 9)$ sowie die parallelen Geraden $g : \vec{x} = \vec{O P} + s \cdot (\begin{array}{c} 3 \\ - 1 \\ 2 \end{array})$ und $h : \vec{x} = \vec{O Q} + t \cdot (\begin{array}{c} 3 \\ - 1 \\ 2 \end{array})$ mit $s, t \in ℝ$ .
Zeigen Sie, dass $g$ und $h$ nicht identisch sind. (2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehung zwischen zwei Geraden
Ortsvektor einsetzen
Ortsvektor von $g$ : $(\begin{array}{c} 2 \\ 0 \\ 1 \end{array})$
$h : \vec{x} = (\begin{array}{c} 2 \\ 4 \\ 9 \end{array}) + t \cdot (\begin{array}{c} 3 \\ - 1 \\ 2 \end{array})$
Setze nun einen Punkt der ersten Gerade in die Gleichung der zweiten Gerade ein.
Dafür wird meist der Ortsvektor genommen.
$(\begin{array}{c} 2 \\ 0 \\ 1 \end{array}) = (\begin{array}{c} 2 \\ 4 \\ 9 \end{array}) + t \cdot (\begin{array}{c} 3 \\ - 1 \\ 2 \end{array})$
Schreibe dies wieder aus und berechne für jede Zeile das $t$ .
$| \begin{array}{l} 2 = 2 + 3 t \\ 0 = 4 - 1 t \\ 1 = 9 + 2 t \end{array} \begin{array}{c} \to \\ \to \\ \to \end{array} \begin{array}{l} t = 0 \\ t = 4 \\ t = - 4 \end{array}$
Sobald sich unterschiedliche Werte für $t$ ergeben ist das Gleichungssystem nicht lösbar. Der Ortsvektor der Gerade $g$ liegt also nicht auf der Geraden $h$ .
Also sind die beiden Geraden nicht identisch und sind daher parallel.
Prüfe, ob die Richtungsvektoren linear abhängig oder unabhängig sind.
Setze den Ortsvektor eines Punktes der ersten Geraden in die Gleichung der zweiten Gerade ein.

Bestimmen Sie eine Gleichung der Geraden, die parallel zu $g$ und $h$ ist und die Strecke $P Q$ im Punkt $T$ schneidet, wobei $3 \cdot | P T | = | Q T |$ ist. (3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung in der analytischen Geometrie
Richtungsvektor der Geraden
Da die gesuchte Gerade parallel zu $g$ und $h$ ist, hat sie denselben Richtungsvektor wie $g$ und $h$ , also $(\begin{array}{c} 3 \\ - 1 \\ 2 \end{array}) .$
Punkt $T$ finden
$\vec{P} = (\begin{array}{c} 2 \\ 0 \\ 1 \end{array}), \vec{Q} (\begin{array}{c} 2 \\ 4 \\ 9 \end{array}) \Rightarrow \vec{P Q} = (\begin{array}{c} 0 \\ 4 \\ 8 \end{array})$
Der Punkt $T$ liegt auf der gesuchten Geraden und er teilt die Strecke $P Q$ im Verhältnis $1 : 3.$ Das bedeutet, dass der Ortsvektor von $T$ auf der Linie von $P$ nach $Q$ ein Einheit von $P$ und $3$ Einheiten von $Q$ entfernt ist. Daher können wir den Ortsvektor von $T$ wie folgt berechnen:
$\vec{T} = \vec{P} + \frac{1}{4} \cdot \vec{P Q} = (\begin{array}{c} 2 \\ 0 \\ 1 \end{array}) + \frac{1}{4} \cdot (\begin{array}{c} 0 \\ 4 \\ 8 \end{array}) = (\begin{array}{c} 2 \\ 0 \\ 1 \end{array}) + (\begin{array}{c} 0 \\ 1 \\ 2 \end{array}) = (\begin{array}{c} 2 \\ 1 \\ 3 \end{array}) .$
Gerade erstellen
Die Gleichung der gesuchten Geraden hat die Form
$\vec{x} = \vec{O T} + r \cdot (\begin{array}{c} 3 \\ - 1 \\ 2 \end{array}), wobei \vec{O T} = (\begin{array}{c} 2 \\ 1 \\ 3 \end{array}) .$
Daher lautet die Gleichung der gesuchten Geraden:
$\vec{x} = (\begin{array}{c} 2 \\ 1 \\ 3 \end{array}) + r \cdot (\begin{array}{c} 3 \\ - 1 \\ 2 \end{array})$
Bestimme den Richtungsvektor der neuen Geraden.
Bestimme den Ortsvektor $\vec{O T} .$
Bilde die Gerade.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org

$f (x)$	$=$	$0,5 \cdot b^{x}$
	↓	Punkt einsetzen
$2$	$=$	$0,5 \cdot b^{1}$	$: 0,5$
$4$	$=$	$b$

$f (x)$	$=$	$(x^{2} - 3 x + 2) (x + 3)$
$f {(x)}_{}$	$=$	$x^{3} + 3 x^{2} - 3 x^{2} - 9 x + 2 x + 6$
$f (x)$	$=$	$x^{3} - 7 x + 6$

$x^{2} - 2 x - 24$	$=$	$0$
	↓	$p q - F o r m e l$
$x_{1,2}$	$=$	$- \frac{(- 2)}{2} \pm \sqrt{{(\frac{(- 2)}{2})}^{2} - (- 24)}$
$x_{1,2}$	$=$	$1 \pm \sqrt{{(1)}^{2} + 24}$
$x_{1,2}$	$=$	$1 \pm \sqrt{25}$

"obere Funktion minus untere Funktion"
	↓
$A$	$=$	$\int_{m}^{0} m x - x^{2} d x$
	↓	Stammfunktion bilden
	$=$	${[\frac{m}{2} x^{2} - \frac{1}{3} x^{3}]}_{m}^{0}$
	↓	Grenzen einsetzen
	$=$	$0 - (\frac{m^{3}}{2} - \frac{m^{3}}{3})$
	$=$	$- \frac{m^{3}}{6}$

$5 z$	$=$	$35$	$: 5$
$z$	$=$	$7$

Pflichtteil - Analysis & Analytische Geometrie / Lineare Algebra

Aufgabe P1

Anfangswert a

Wachstumsrate b

Verschiebung um 2 in negativer x-Richtung

Umformung von g(x)

Aufgabe P2

Linearfaktoren bilden

Linearfaktordarstellung

Ausmultiplizieren

Nullstellen berechnen

2. Ableitung

Hinreichende Bedingung

Aufgabe P3

Schnittpunkte berechnen

Fläche berechnen

Fläche mit dem Inhalt 36

Aufgabe P4

Vektoren bilden

Länge berechnen

Flächeninhalt berechnen

Flächeninhalt gleich 35

Aufgabe P5

Ortsvektor einsetzen

Richtungsvektor der Geraden

Punkt T finden

Gerade erstellen

Anfangswert $a$

Wachstumsrate $b$

Verschiebung um $2$ in negativer $x$ -Richtung

Umformung von $g (x)$

$2$ . Ableitung

Fläche mit dem Inhalt $36$

Punkt $T$ finden