Aufgaben zum Schätzen von Quadratwurzeln

1
Schätze den Wert von $\sqrt{7}$ .
Berechne dazu die ersten fünf Schritte der Intervallschachtelung und schätze anschließend den Wert von $\sqrt{7}$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Intervallschachtelung
Die Methode der Intervallschachtelung ist eine Möglichkeit der Abschätzung von Werten von Wurzeln.
Überlege dir für den ersten Schritt ein Intervall, in dem der Wert von $\sqrt{7}$ liegen kann. Nutze dazu bereits bekannte Wurzelwerte.
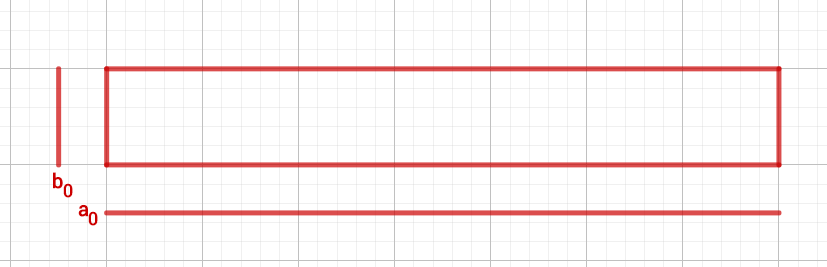
1. Schritt
Du kennst bereits die Werte von:
$\sqrt{4}$ und $\sqrt{9}$
Daraus kannst du die erste Abschätzung machen:
$\begin{matrix} 2^{2} & < & 7 & < & 3^{2} \\ 4 & < & 7 & < & 9 \end{matrix}$
daraus folgt wiederum:
$\sqrt{4} < \sqrt{7} < \sqrt{9}$
Das bedeutet, der Wert von $\sqrt{7}$ liegt im Intervall:
$I_{0} =] 2; 3 [$
Die nächsten Schritte laufen immer in der gleichen Reihenfolge ab. Du bildest zuerst den Mittelwert der alten Intervallgrenzen. Dieser Wert bildet wiederum eine der neuen Intervallgrenzen. Die andere bleibt erhalten.
Ob der neue Wert die obere oder untere Intervallgrenze ist, entscheidest du wie folgt: quadriere den Mittelwert und vergleiche diesen Wert mit der $7$ .
Wenn er
größer als $7$ ist, bildet er die neue Obergrenze
kleiner als $7$ ist, bildet er die neue Untergrenze
Eine ausführliche Erklärung dieser Schritte findest du hier.
2. Schritt
$I_{0} =] 2; 3 [$
Bilde den Mittelwert der Intervallgrenzen von $I_{0}$ !
$\frac{2 + 3}{2} = 2,5$
Berechne das Quadrat von $2,5$ und vergleiche es mit $7$ .
${2,5}^{2} = 6,25$
$6,25 < 7 < 9$
${2,5}^{2} < 7 < 3^{2}$
Definiere nun das neue Intervall!
$I_{1} =] 2,5; 3 [$
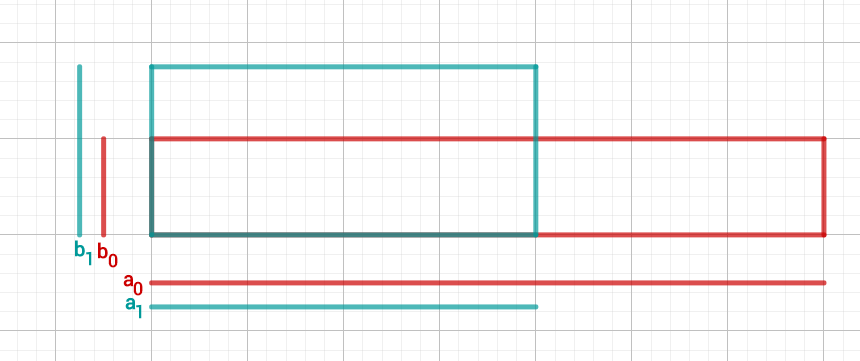
3. Schritt
$I_{1} =] 2,5; 3 [$
Bilde den Mittelwert der Intervallgrenzen von $I_{1}$ !
$\frac{2,5 + 3}{2} = 2,75$
Berechne das Quadrat des Mittelwertes und vergleiche es mit $7$ .
${2,75}^{2} = 7,56$
$\begin{array}{cccc} 6,25 & < & 7 & < & 7,56 \\ {2,5}^{2} & < & 7 & < & {2,75}^{2} \end{array}$
Definiere nun das neue Intervall!
$I_{2} =] 2,5; 2,75 [$
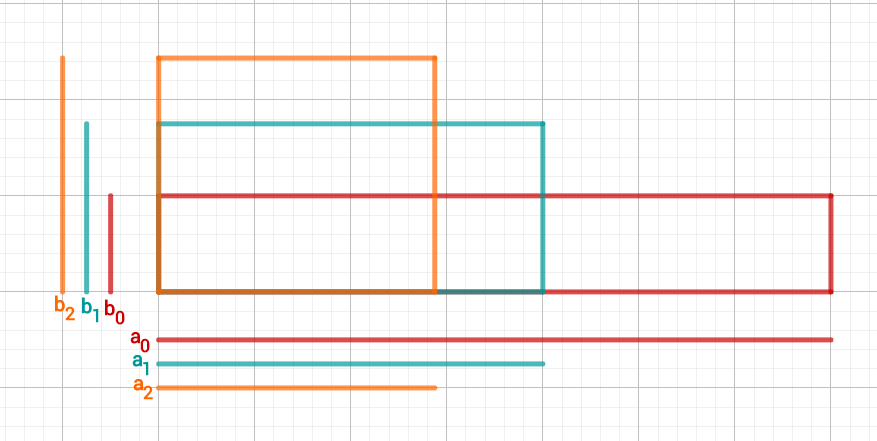
4. Schritt
$I_{2} =] 2,5; 2,75 [$
Bilde den Mittelwert der Intervallgrenzen von $I_{2}$ !
$\frac{2,5 + 2,75}{2} = 2,625$
Berechne das Quadrat von $2,625$ und vergleiche es mit $7$ .
${2,625}^{2} \approx 6,89$
$\begin{array}{ccc} 6,89 & < & 7 & < & 7,56 \\ {2,625}^{2} & < & 7 & < & {2,75}^{2} \end{array}$
Definiere nun das neue Intervall!
$I_{3} =] 2,625; 2,75 [$
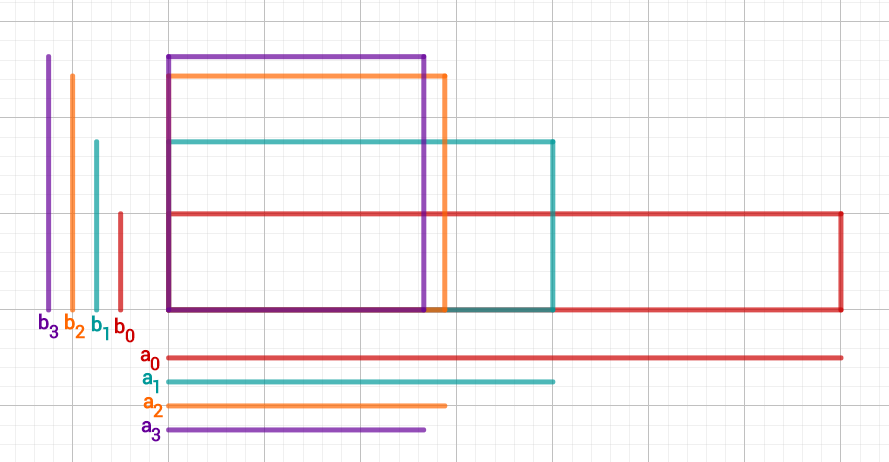
5. Schritt
$I_{3} =] 2,625; 2,75 [$
Bilde den Mittelwert der Intervallgrenzen von $I_{2}$ !
$\frac{2,625 + 2,75}{2} = 2,6875$
Berechne das Quadrat des Mittelwerts und vergleiche mit $7$ .
${2,6875}^{2} \approx 7,22$
${2,625}^{2} < 7 < {2,6875}^{2}$
Definiere nun das neue Intervall!
$I_{4} =] 2,625; 2,6875 [$
Nach diesen fünf Schritten wissen wir:
$\sqrt{7} \in I_{4}$
Also: Der Wert von $\sqrt{7}$ liegt zwischen $2,625$ und $2,6875$ .
Abschätzung
Nimm den Mittelwert der letzten Intervallgrenzen als mögliche Abschätzung für den Wert von $\sqrt{7}$ .
$\to \sqrt{7} \approx \frac{2,625 + 2,6875}{2} = 2,65625$
Die Abschätzung von $\sqrt{7}$ ergibt $2,65625$ .
Als Vergleich: Der Taschenrechner rundet auf $2,64575$ .
2
Schätze den Wert von $\sqrt{7}$ .
Berechne dazu die ersten vier Schritte des Heron-Verfahrens und schätze anschließend den Wert von $\sqrt{7}$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Heron-Verfahren
Heron-Verfahren
Das Heron-Verfahren ist eine Methode, um den Wert von Wurzeln (schrittweise) abzuschätzen.
Du suchst ein Quadrat, dessen Flächeninhalt genau dem Radikanden $7$ entspricht. Dazu bildest du zuerst ein Rechteck, dessen Seiten du Schritt für Schritt veränderst.
1. Schritt
Das erste Rechteck findest du, indem du einen Teiler des Radikanden suchst und dann die zweite Seite durch Auflösen der Formel für den Flächeninhalt für Rechtecke.
$A = a \cdot b$
$A$ entspricht dem Radikanden. In unserem Fall ist $A = 7$ und nur durch $1$ und sich selbst $7$ teilbar. Daraus ergeben sich unsere Anfangswerte $a_{0}$ und $b_{0}$ .
$a_{0} = 7$
$b_{0} = 1$
Im Bild unten siehst du das anfängliche Rechteck.
Die nächsten Schritte laufen immer in der folgenden Reihenfolge ab:
Zuerst bildest du den Mittelwert der alten Werte und berechnest daraus dein neues $a$ .
$b$ findest du, indem du $b = \frac{A}{a}$ rechnest und dort das neue $a$ einsetzt und den Radikanden für $A$ .
Eine ausführliche Erklärung dieser Schritte findest du hier.
2. Schritt
Bilde den Mittelwert von $a_{0}$ und $b_{0}$ .
$a_{1} = \frac{a_{0} + b_{0}}{2} = \frac{7 + 1}{2} = 4$
Berechne anschließend $b_{1}$ .
$b_{1} = \frac{A}{a_{1}} = \frac{Radikand}{a_{1}} = \frac{7}{4} = 1,75$
Deine neuen Werte:
$a_{1} = 4$
$b_{1} = 1,75$
Im Bild unten siehst du das ursprüngliche Rechteck und das neue, das sich mehr einem Quadrat angenähert hat.
3. Schritt
Bilde den Mittelwert von $a_{1}$ und $b_{1}$ .
$a_{2} = \frac{a_{1} + b_{1}}{2} = \frac{4 + 1,75}{2} = 2,875$
Berechne anschließend $b_{2}$ .
$\begin{array}{l} b_{2} = \frac{A}{a_{2}} = \frac{Radikand}{a_{2}} \\ = \frac{7}{2,875} = 2,4348 \end{array}$
Deine neuen Werte sind:
$a_{2} = 2,875$
$b_{2} = 2,4348$
Im Bild unten siehst du die Veränderung der Rechtecke.
4. Schritt
Bilde den Mittelwert von $a_{2}$ und $b_{2}$ .
$a_{3} = \frac{a_{2} + b_{2}}{2} = \frac{2,875 + 2,4348}{2} = 2,6548$
Berechne nun $b_{3}$ .
$\begin{array}{l} b_{3} = \frac{A}{a_{3}} = \frac{Radikand}{a_{3}} \\ = \frac{7}{2,6548} = 2,6367 \end{array}$
Deine endgültigen Werte sind $a_{3} = 2,6548$ und $b_{3} = 2,6367$ .
Wie dir auffällt, haben sich die beiden Werte sehr stark angenähert.
Im Bild unten siehst du die Veränderung der Rechtecke. Das letzte (lila) ist schon nah an einem Quadrat.
Abschätzung
Für die Abschätzung bildest du nochmal den Mittelwert zwischen den beiden letzten Seiten.
$\sqrt{7} \approx \frac{2,6548 + 2,6367}{2} = 2,64575$
Zum Vergleich: Wenn du den Wert im Taschenrechner berechnest, erhältst du den gerundeten Wert: $2,64575$ .
3
Überlege dir zwei natüliche Zahlen, zwischen denen $\sqrt{37}$ liegt. Versuche dabei so nah wie möglich an $\sqrt{37}$ heran zu kommen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wurzel
$37$ liegt zwischen den Quadratzahlen $36 = 6^{2}$ und $49 = 7^{2}$ .
$\sqrt{37}$ liegt also zwischen $\sqrt{36} = 6$ und $\sqrt{49} = 7$ .
Überlege zwischen welchen Quadratzahlen die 37 liegt.
4
Schätze den Wert von $102^{2}$ und $\sqrt{102}$ indem du sie durch geeignetere Werte ersetzt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wurzelziehen
Zuerst wird 102 durch 100 ersetzt.
Dabei ist $100^{2} = 100 \cdot 100 = 10000$
und $\sqrt{100} = \sqrt{10^{2}} = 10$
$102^{2}$ ist also etwas größer als $10000$ und $\sqrt{102}$ ist etwas größer als $10$ .
5
Du hast deinen Taschenrechner vergessen und brauchst das Ergebnis von $\sqrt{56}$ . Schätze den Wert durch geschicktes Überlegen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wurzelziehen
Gesucht ist das Ergebnis von $\sqrt{56}$ , also eine Zahl, die man mit sich selbst malnimmt und dann $56$ erhält. $56$ ist nun allerdings keine Quadratzahl, die man auswendig kennt. Doch es gibt Quadratzahlen, die in der Nähe von $56$ liegen.
$49 = 7 \cdot 7$
$64 = 8 \cdot 8$
$56$ liegt zwischen den Quadratzahlen $49$ und $64$ . Das bedeutet, dass der Wert von $\sqrt{56}$ zwischen $7$ und $8$ liegen muss.
Die Quadratzahlen $49$ und $64$ sind ungefähr gleich weit weg von $56$ . Aus diesem Grund liegt der Wert der Wurzel in der Nähe von $7,5$ .
$\sqrt{56} \approx 7,5$
6
Sara und ihr älterer Bruder Markus führen ein Gespräch nach der Schule. Dabei bringt Markus seine kleine Schwester zum Nachdenken. Kannst du Sara helfen die Aufgabe zu lösen?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wurzelziehen
Die benachbarten Quadratzahlen von 20 sind:
$16 < 20 < 25 16 = 4 \cdot 4 = 4^{2} < 20 < 5^{2} = 5 \cdot 5 = 25$
Die Zahl 20 liegt zwischen den Quadratzahlen 16 und 25. Also gilt für die Quadratwurzel von 20:
$\sqrt{4^{2}} < \sqrt{20} < \sqrt{5^{2}} 4 < \sqrt{20} < 5$
Die Zahl $\sqrt{𝟐𝟎}$ liegt zwischen den natürlichen Zahlen 4 und 5.
Da die Quadratzahlen 16 und 25 ungefähr gleich weit von der 20 entfernt sind, liegt die $\sqrt{20}$ ungefähr in der Mitte von 4 und 5.
$\sqrt{𝟐𝟎} \approx 𝟒,𝟓$
Die Quadratwurzel von 20 ist ungefähr 4,5.
In dieser Aufgabe sollst du näherungsweise $\sqrt{20}$ bestimmen. Das heißt, du suchst eine Zahl, die mit sich selbst multipliziert 20 ergibt. Da jedoch 20 keine Quadratzahl ist, ist es geschickt sich zunächst einmal zu überlegen zwischen welchen Quadratzahlen die 20 liegt.