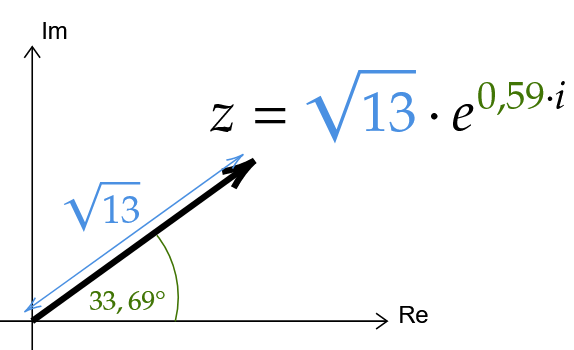
Komplexe Zahlen in Exponentialform
Eine komplexe Zahl kann in der Exponentialform dargestellt werden:
Dahinter steckt die eulersche Formel
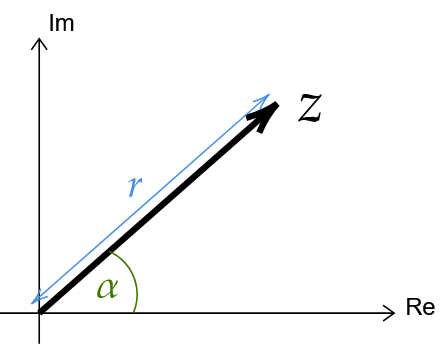
Darstellung einer komplexen Zahl mit Betrag und dem Winkel
Dabei sind
der Betrag der komplexen Zahl (Strecke von Zahl bis zum Ursprung)
der Winkel zwischen und der x-Achse.
Geometrische Interpretation
Geometrisch gesehen haben und in der Exponentialform dieselbe Bedeutung wie in der Polarform einer komplexen Zahl:
entspricht in der Gaußschen Zahlenebene dem Abstand der komplexen Zahl zum Ursprung.
ist der von der Strecke mit der -Achse eingeschlossene Winkel.
Beispiel
Die komplexe Zahl kann auch anders dargestellt werden.
Für die Darstellung durch die Exponentialform muss die Strecke und der Winkel berechnet werden:
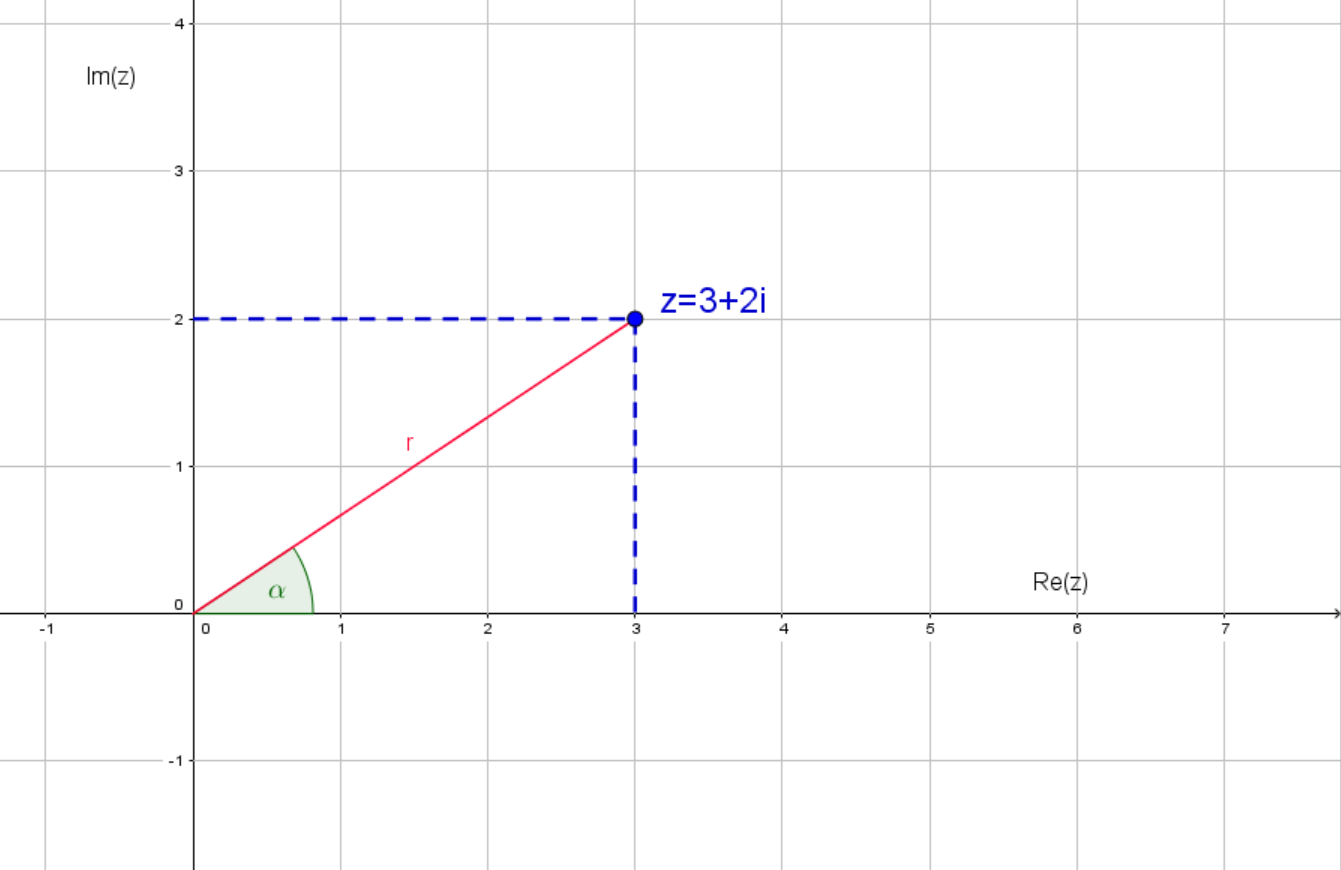
Darstellung der komplexen Zahl
Zusammengesetzt ist die Exponentialdarstellung